Generalized Principal Component Analysis GPCA Ren Vidal Dept

Generalized Principal Component Analysis (GPCA) René Vidal Dept. of EECS UC Berkeley

Research: Control and Robotics n Control & Hybrid Systems n n Controller Synthesis for Discrete-Time Hybrid Systems Computation of Reachable Sets Observability and Identification of Linear Hybrid Systems Robotics Vision-based landing of a UAV Pursuit-Evasion Games Omnivision-based formation control 8

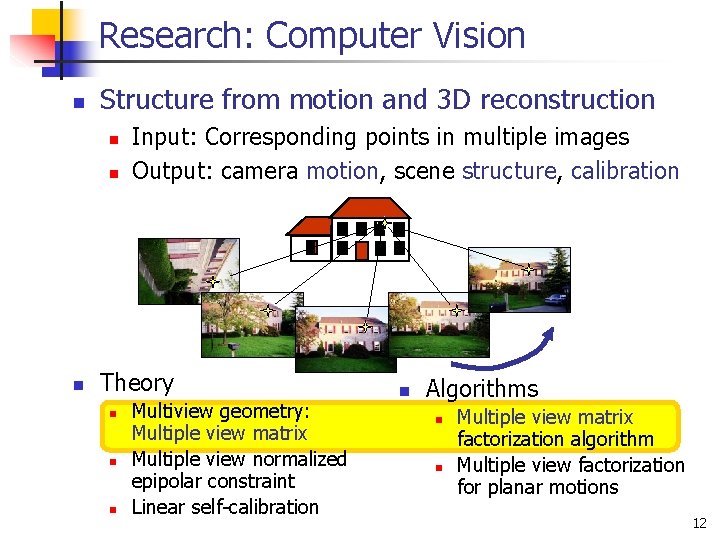
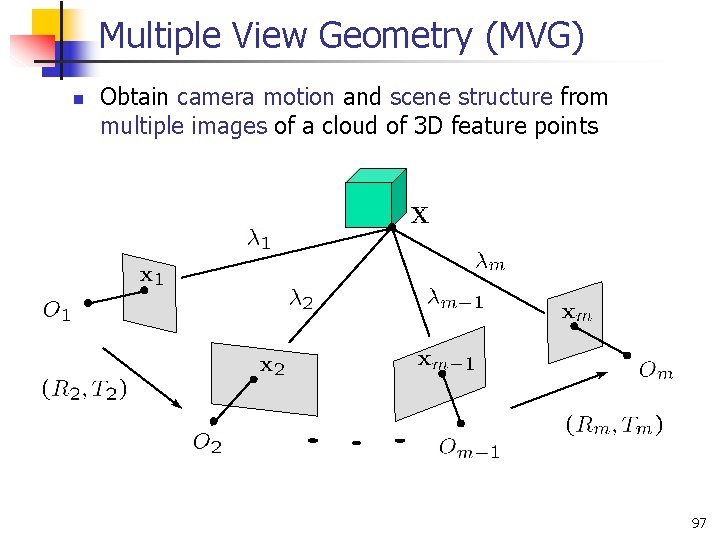
Research: Computer Vision n Structure from motion and 3 D reconstruction n Input: Corresponding points in multiple images Output: camera motion, scene structure, calibration Theory n n n Multiview geometry: Multiple view matrix Multiple view normalized epipolar constraint Linear self-calibration n Algorithms n n Multiple view matrix factorization algorithm Multiple view factorization for planar motions 12

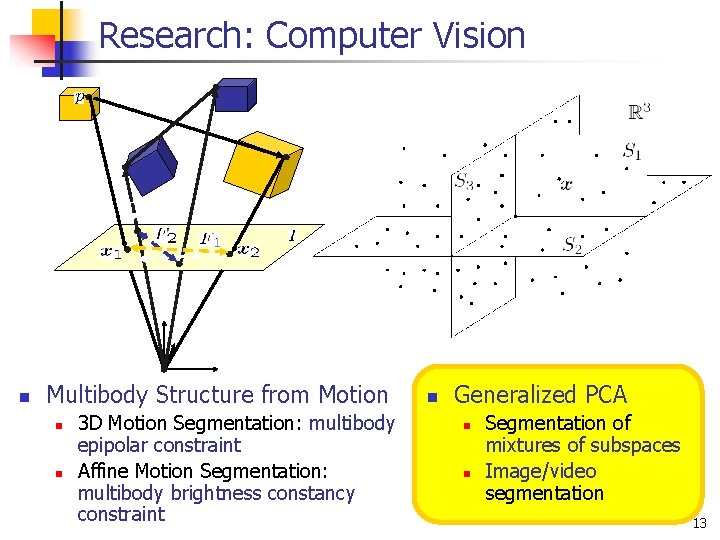
Research: Computer Vision n Multibody Structure from Motion n n 3 D Motion Segmentation: multibody epipolar constraint Affine Motion Segmentation: multibody brightness constancy constraint n Generalized PCA n n Segmentation of mixtures of subspaces Image/video segmentation 13

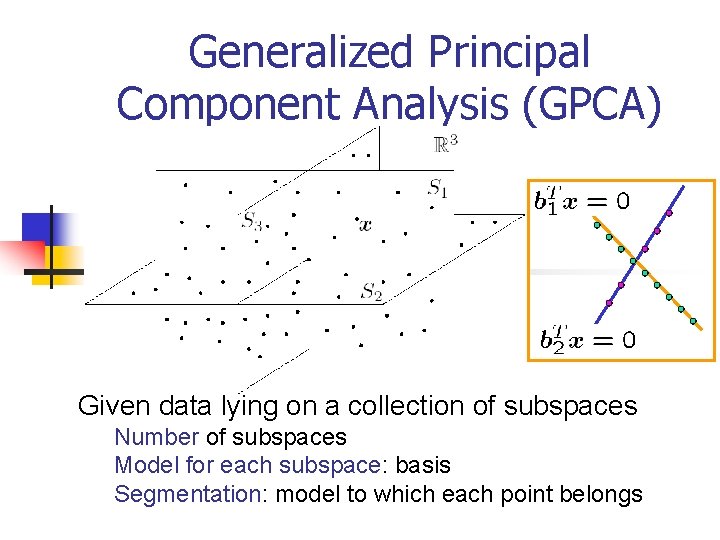
Principal Component Analysis (PCA) n Identify a linear subspace S from sample points Basis for S n Applications: data compression, regression, image analysis (eigenfaces), pattern recognition 16

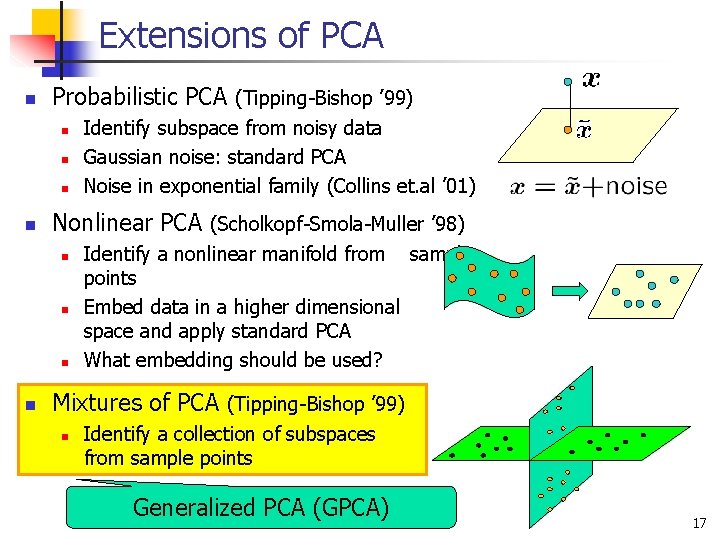
Extensions of PCA n Probabilistic PCA (Tipping-Bishop ’ 99) n n Nonlinear PCA (Scholkopf-Smola-Muller ’ 98) n n Identify subspace from noisy data Gaussian noise: standard PCA Noise in exponential family (Collins et. al ’ 01) Identify a nonlinear manifold from sample points Embed data in a higher dimensional space and apply standard PCA What embedding should be used? Mixtures of PCA (Tipping-Bishop ’ 99) n Identify a collection of subspaces from sample points Generalized PCA (GPCA) 17

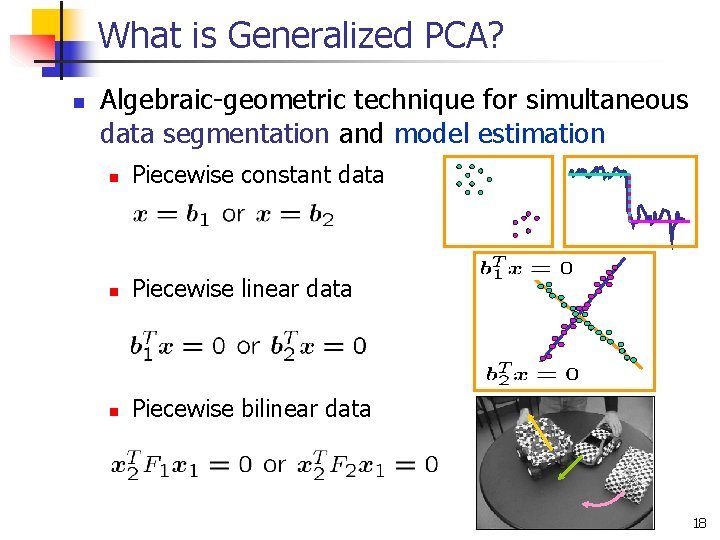
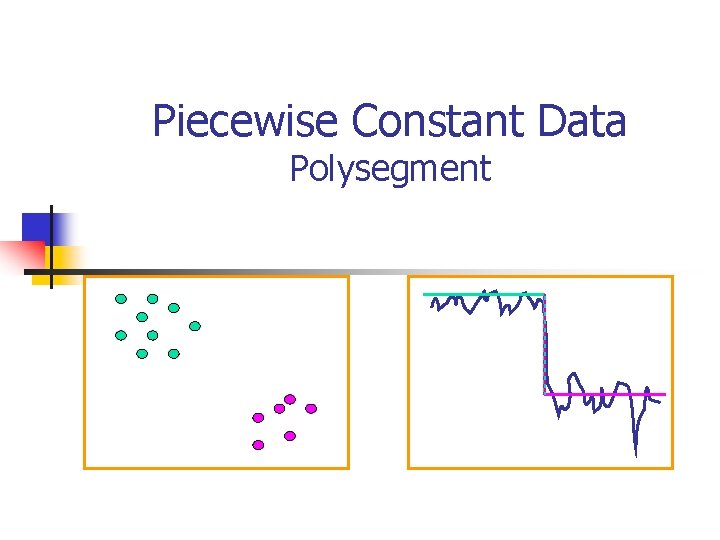
What is Generalized PCA? n Algebraic-geometric technique for simultaneous data segmentation and model estimation n Piecewise constant data n Piecewise linear data n Piecewise bilinear data 18

Some possible applications of GPCA n Segmentation n Image segmentation n n Recognition n Faces (Eigenfaces) n n n Man - Woman Human activities n n Intensity Color Motion Texture Running, walking Identification of hybrid systems Data compression UCLA database CMU database 20

Prior work on mixtures of PCA n Chicken-and-egg problem n n n Geometric approaches n n n Given segmentation, estimate subspaces Given subspaces, segment the data Segment data using similarity matrices + clustering Apply standard PCA to each group Probabilistic approaches n n (Tipping-Bishop ‘ 99) Generative model: data membership + subspace model Identify subspaces using Expectation Maximization n (Boult et al. , Costeira et al. , Kanatani) E-step: estimate membership given model parameters M-step: estimate parameters given membership How to initialize iterative algorithms? 23

Our approach to segmentation (GPCA) n Towards an analytic solution to segmentation n n We propose an algebraic geometric approach to data segmentation n Number of groups Groups = degree of a polynomial ≈ roots of a polynomial = polynomial factorization In the absence of noise n n Can we estimate ALL models simultaneously using ALL data? When can we do so analytically? In closed form? Is there a formula for the number of models? Use constraints that are independent on the segmentation There is a unique solution which is closed form iff ngroups ≤ 4 The exact solution can be computed using linear algebra In the presence of noise n n Algebraic solution can be used to initialize EM Derive a maximum likelihood algorithm for zero-mean Gaussian noise in which the E-step is algebraically eliminated 24

Piecewise Constant Data Polysegment

Piecewise constant data n Number of groups? 27

Piecewise constant data n For n groups n Number of groups n Groups n Solution is unique if n Solution is closed form if and only if 29

Piecewise constant data n What about dimension 2? n What about higher dimensions? n n n Complex numbers in higher dimensions? How to find roots of a polynomial of quaternions? Instead n n Project data onto one or two dimensional space Apply same algorithm to projected data 30

Intensity-based image segmentation n Apply GPCA to vector of image intensities N=#pixels n n=3 groups n n n Black Gray White 32

Intensity-based image segmentation Black group Gray group White group 147 x 221 Time: 2 (sec) 10 (sec) 0. 4 (sec) 33

Texture-based image segmentation Polysegment Human 37

Texture-based image segmentation Polysegment Human 40

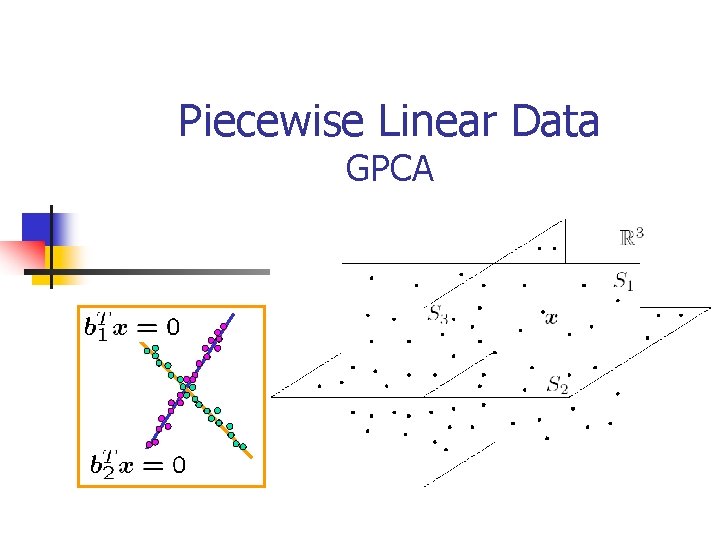
Piecewise Linear Data GPCA

K-dimensional Segmentation (GPCA) n Identify n n -dimensional subspaces of : dimension of ambient space (known) : dimension of each subspace (unknown) : number of subspaces (unknown) : normal to each subspace (unknown) n Embed data onto. n n Veronese map 42

K-dimensional Segmentation: Projection n n Segmentation of the data is preserved by a projection onto a smaller dimensional space GPCA can be reduced to segmentation of subspaces of dimension 1 less than ambient space n n n Lines in Planes in What is the dimension ? 44

K-dimensional Segmentation n 1 -dimensional case n K-dimensional case 45

K-dimensional Segmentation n 1 -dimensional case n K-dimensional case Estimate all models: coefficients of a polynomial Estimate number models: rank of a matrix Estimate individual models: roots/factors of the polynomial 46

Polynomial factorization Theorem: Generalized PCA [Vidal et al. 2003] n Find roots of polynomial of degree n Solve n in one variable K-2 linear systems in n variables 47

GPCA algorithm 1. Compute number of groups from rank data matrix 2. Embed each data point into higher-dimensional space 3. Compute all subspaces from nullspace of data matrix 4. Compute the subspace normals 1. Roots poly 2. Linear system 48

Optimal GPCA n Zero-mean Gaussian noise Minimize distance from noisy data to noise free data subject to segmentation constraints n Using Langrange optimization n After some algebra n 49

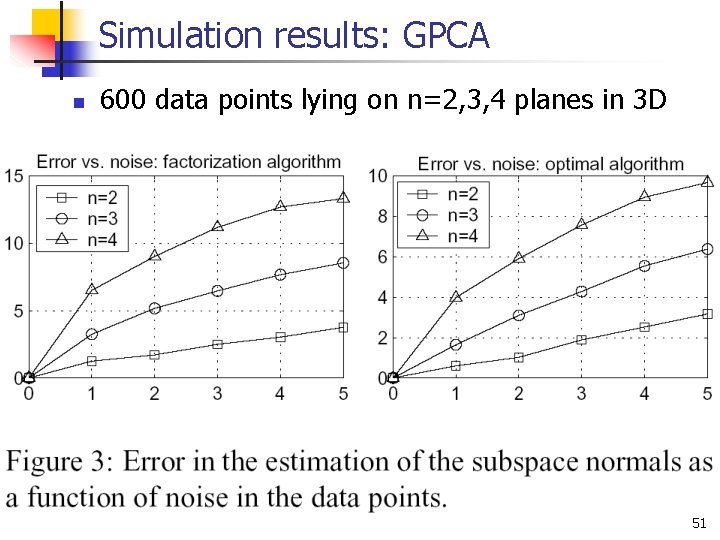
Simulation results: GPCA n 600 data points lying on n=2, 3, 4 planes in 3 D 51

2 D flow-based motion segmentation n Two motions n n Camera panning to the right Car translating to the right http: //www. cs. otago. ac. nz/research/vision/Research/ 53

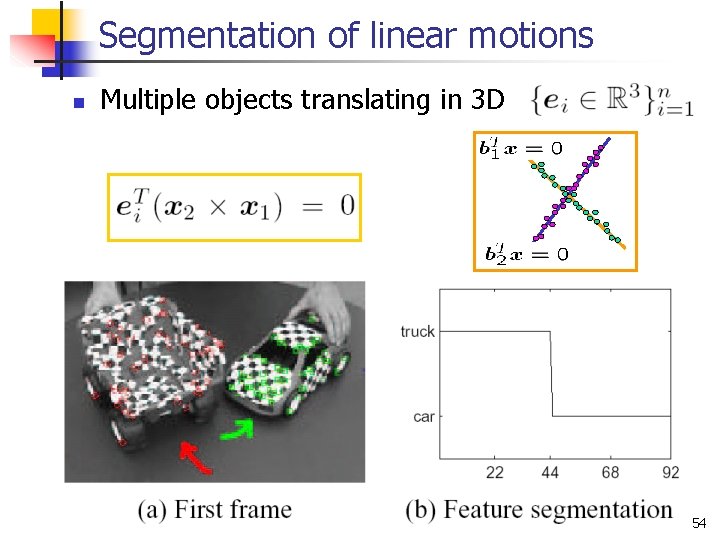
Segmentation of linear motions n Multiple objects translating in 3 D 54

Piecewise Bilinear Data Multibody structure from motion

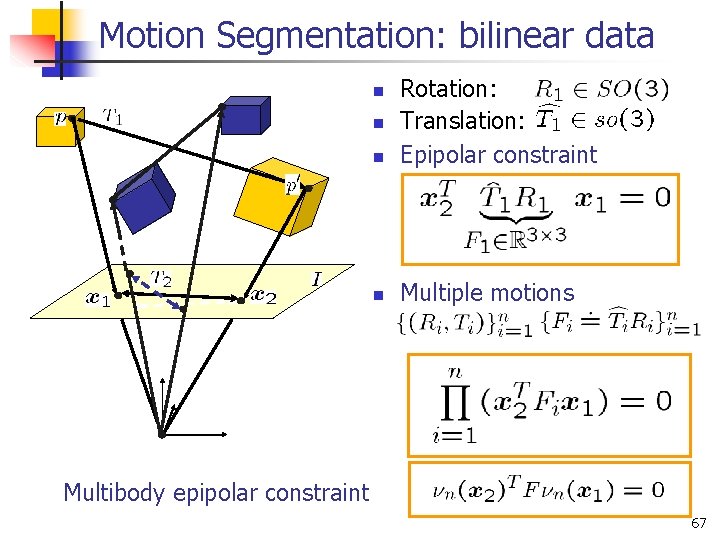
Motion Segmentation: bilinear data n Rotation: Translation: Epipolar constraint n Multiple motions n n Multibody epipolar constraint 67

Estimation of fundamental matrices Multibody epipolar constraint Given rank condition Embedding Lifting n linear system F Embedding Theorem: Multibody structure from motion [Vidal et al. ] n n Factorization of bilinear forms can be reduced to factorization of linear forms Estimation of fundamental matrices can be reduced to GPCA 70

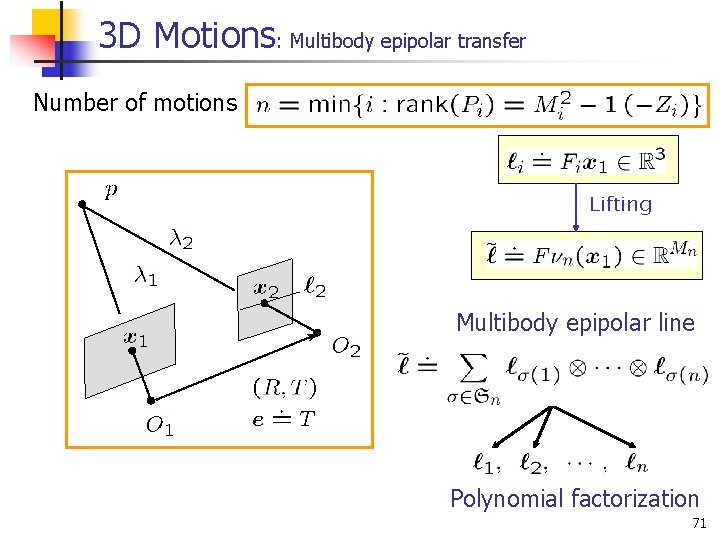
3 D Motions: Multibody epipolar transfer Number of motions Lifting Multibody epipolar line Polynomial factorization 71

3 D Motions: Multibody epipole Lifting n The multibody epipole is the solution of the linear system n n Number of distinct epipoles Epipoles are obtained using polynomial factorization 72

3 D Motions: Fundamental matrices n Columns of are epipolar lines n Polynomial factorization to compute them up to scale n Scales can be computed linearly 73

Comparison of 1 and n bodies 74

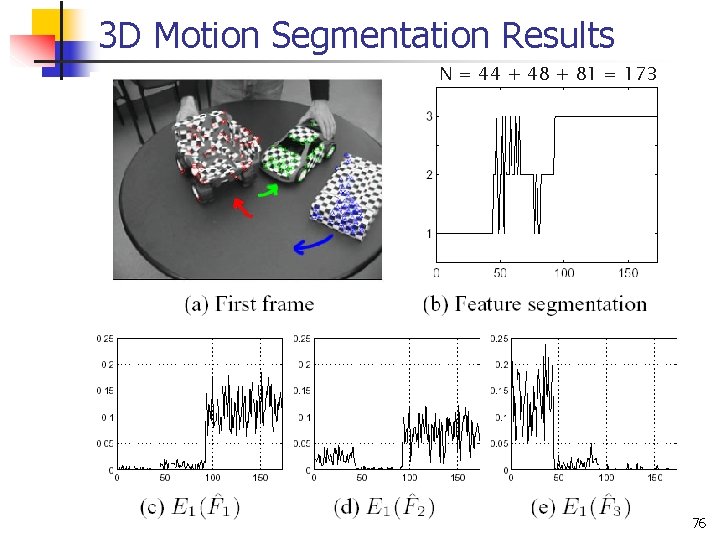
3 D Motion Segmentation Results N = 44 + 48 + 81 = 173 76

Affine Motion Segmentation Results The affine motion model 77

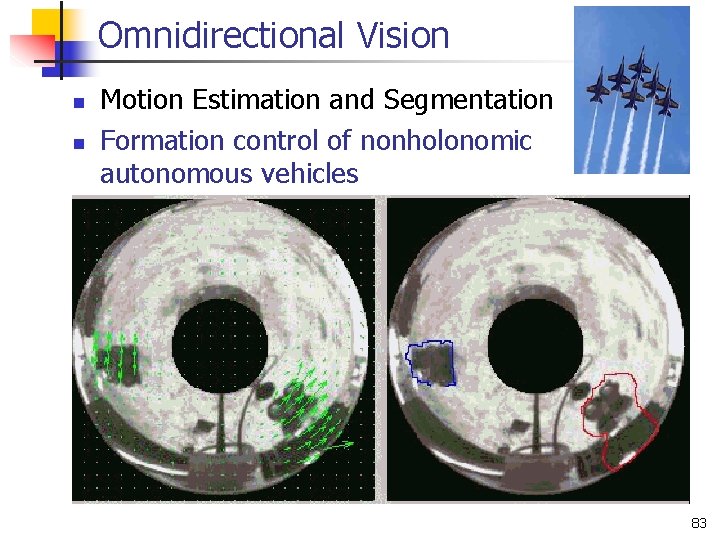
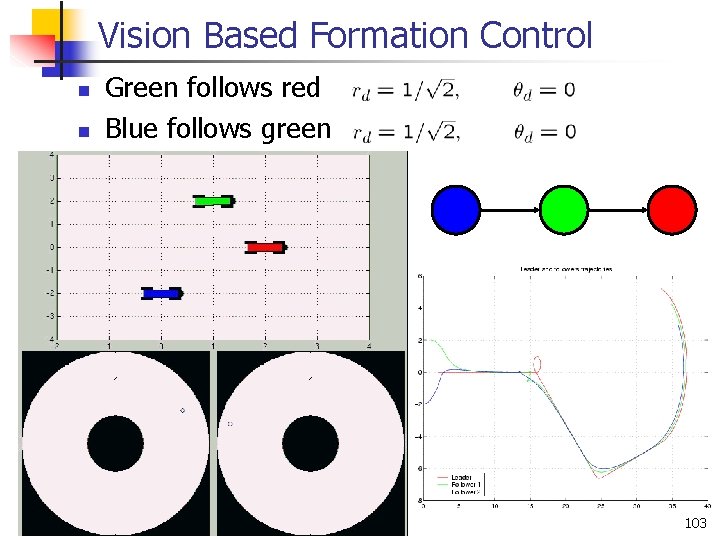
Omnidirectional Vision n n Motion Estimation and Segmentation Formation control of nonholonomic autonomous vehicles 83

Conclusions n There is an algebraic/geometric solution to simultaneous model estimation and data segmentation for n n n Solution based on n Mixtures of subspaces: linear constraints Motion segmentation: bilinear constraints Polynomial factorization: linear algebra Solution is closed form if ngroups ≤ 4 Showed applications in n n Image segmentation: intensity and texture Video segmentation: affine and 3 D motion segmentation 89

Ongoing work and future directions n Statistical Geometry = Geometry + Statistics n n n Applications of GPCA in Computer Vision n n Robust GPCA Relations to other methods: Kernel PCA, etc. Model selection Estimating manifolds from sample data points Optical flow estimation and segmentation Motion segmentation: multiple views Shape recognition: faces A geometric/statistical theory of segmentation? 90

Dynamic GPCA: Recognition/Synthesis of Human Motion Recognition/Synthesis of Dynamic Textures n Given image data n n Estimate a mixture of linear dynamical models (linear hybrid systems) Use the models recognize n n n Use the models to synthesize n UCLA database Human activity Dynamic texture n human motion dynamic textures 93

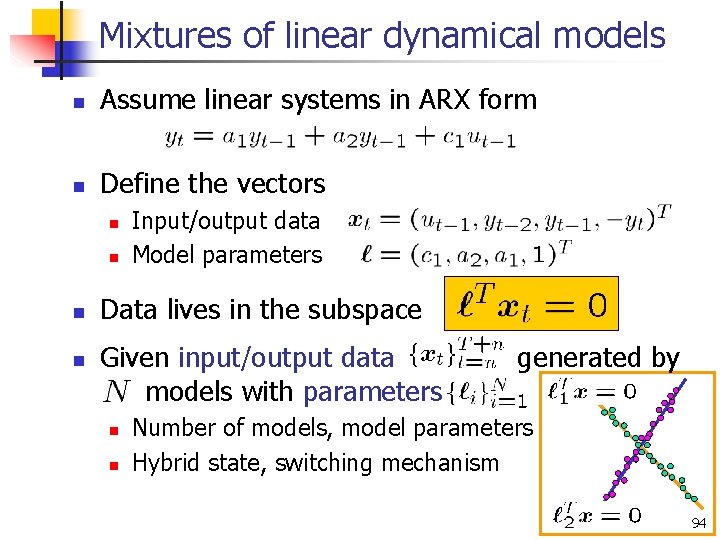
Mixtures of linear dynamical models n Assume linear systems in ARX form n Define the vectors n n Input/output data Model parameters Data lives in the subspace Given input/output data models with parameters n n generated by Number of models, model parameters Hybrid state, switching mechanism 94

Thanks n Pursuit-Evasion Games n n n Jin Kim David Shim Computer Vision n n Vision Based Landing n n Omid Shakernia Cory Sharp n n Control/Hybrid Systems n n n Formation Control n n Omid Shakernia Noah Cowan n Stefano Soatto, UCLA Yi Ma, UIUC Jana Kosecka, GMU John Oliensis, NEC John Lygeros, Cambridge Shawn Schaffert Research Advisor n Shankar Sastry 96

Multiple View Geometry (MVG) n Obtain camera motion and scene structure from multiple images of a cloud of 3 D feature points 97

MVG: Anatomy of cases (state of the art) surface curve practice line algorithm theory 2 views 3 views 4 views point affine projective Euclidean algebra geometry optimization m views 98

MVG: A need for unification surface curve practice line algorithm theory 2 views 3 views 4 views point affine projective Euclidean algebra geometry rank deficiency of Multiple View Matrix optimization m views 99

MVG: The Multiple View Matrix n Relationship between first and i-th views n Theorem: [Rank deficiency of Multiple View Matrix] (generic) (degenerate) n Theorem: [Dependency of multilinear constraints] n Constraints among more than three views are algebraically dependent (quadrilinear in particular) 100

Texture segmentation n Given a static image, determine n n Number of groups Segmentation: pixels that have the same texture 101

Generalized Principal Component Analysis (GPCA) Given data lying on a collection of subspaces Number of subspaces Model for each subspace: basis Segmentation: model to which each point belongs

Vision Based Formation Control n n Green follows red Blue follows green 103