Generalized Principal Component Analysis GPCA Ren Vidal Center

Generalized Principal Component Analysis GPCA René Vidal Center for Imaging Science Department of Biomedical Engineering Johns Hopkins University

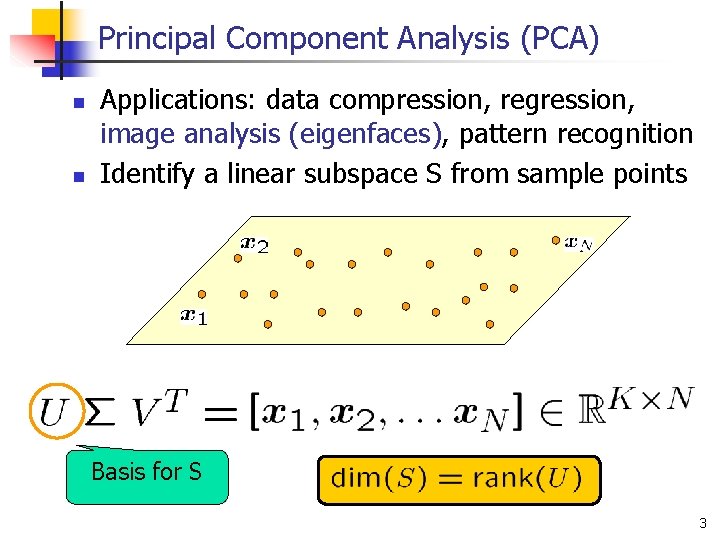
Principal Component Analysis (PCA) n n Applications: data compression, regression, image analysis (eigenfaces), pattern recognition Identify a linear subspace S from sample points Basis for S 3

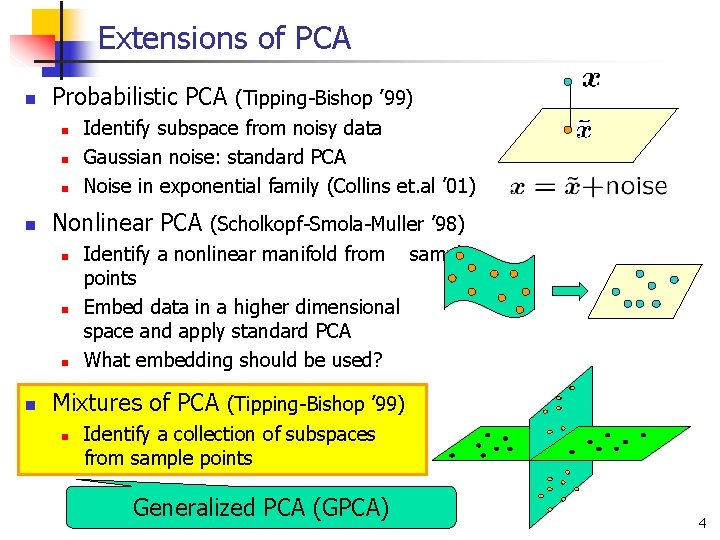
Extensions of PCA n Probabilistic PCA (Tipping-Bishop ’ 99) n n Nonlinear PCA (Scholkopf-Smola-Muller ’ 98) n n Identify subspace from noisy data Gaussian noise: standard PCA Noise in exponential family (Collins et. al ’ 01) Identify a nonlinear manifold from sample points Embed data in a higher dimensional space and apply standard PCA What embedding should be used? Mixtures of PCA (Tipping-Bishop ’ 99) n Identify a collection of subspaces from sample points Generalized PCA (GPCA) 4

Some possible applications of GPCA n Geometry n n Segmentation n n Vanishing points Intensity (black-white) Texture Motion (2 -D, 3 -D) Scene (host-guest) Recognition n Faces (Eigenfaces) n n Dynamic Textures n n Man - Woman Water-steam Image/data compression 5

Generalized Principal Component Analysis n Given points on multiple subspaces, identify n n “Chicken-and-egg” problem n n n Given segmentation, estimate subspaces Given subspaces, segment the data Prior work n n n The number of subspaces and their dimensions A basis for each subspace The segmentation of the data points Iterative algorithms: K-subspace (Ho et al. ’ 03), RANSAC, subspace selection and growing (Leonardis et al. ’ 02) Probabilistic approaches learn the parameters of a mixture model using e. g. EM (Tipping-Bishop ‘ 99): Initialization? n n Geometric approaches: 2 planes in R 3 (Shizawa-Maze ’ 91) Factorization approaches: independent, orthogonal subspaces of equal dimension (Boult-Brown ‘ 91, Costeira-Kanade ‘ 98, Kanatani ’ 01) 6

Our approach to segmentation (GPCA) n We consider the most general case n n Subspaces of unknown and possibly different dimensions Subspaces may intersect arbitrarily (not only at the origin) Subspaces do not need to be orthogonal Multiple subspaces can be represented with multiple homogeneous polynomials n n n Number of subspaces = degree of a polynomial Subspace basis = derivatives of a polynomial Subspace clustering is algebraically equivalent to n n n Polynomial fitting Polynomial differentiation Polynomial division 7

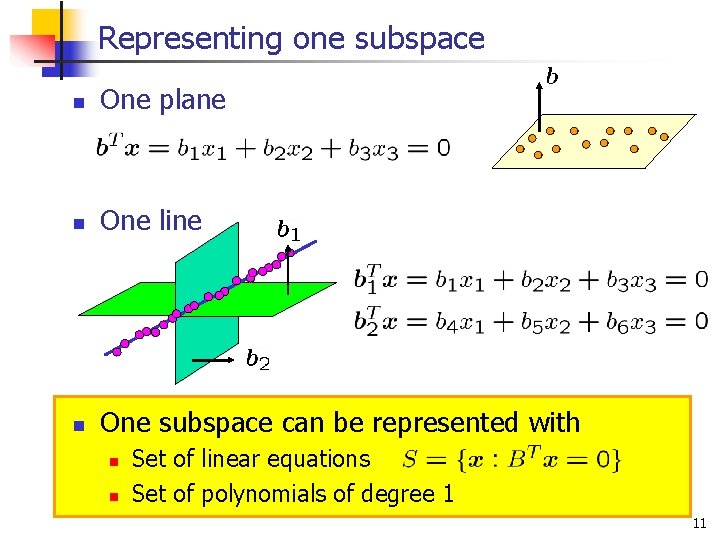
Representing one subspace n One plane n One line n One subspace can be represented with n n Set of linear equations Set of polynomials of degree 1 11

Representing n subspaces n Two planes n One plane and one line n n Plane: Line: De Morgan’s rule n A union of n subspaces can be represented with a set of homogeneous polynomials of degree n 12

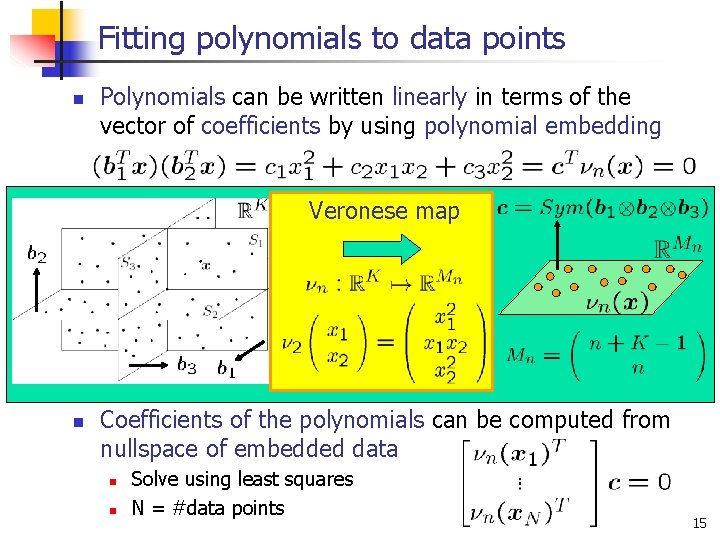
Fitting polynomials to data points n Polynomials can be written linearly in terms of the vector of coefficients by using polynomial embedding Veronese map n Coefficients of the polynomials can be computed from nullspace of embedded data n n Solve using least squares N = #data points 15

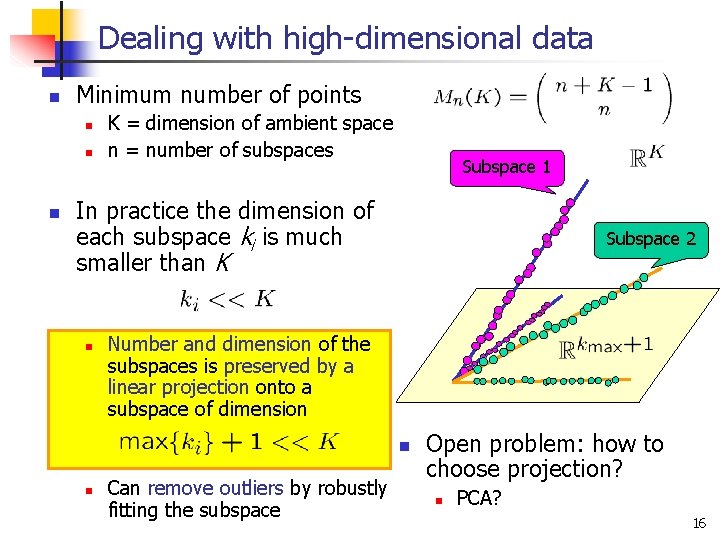
Dealing with high-dimensional data n Minimum number of points n n n K = dimension of ambient space n = number of subspaces Subspace 1 In practice the dimension of each subspace ki is much smaller than K n Subspace 2 Number and dimension of the subspaces is preserved by a linear projection onto a subspace of dimension n n Can remove outliers by robustly fitting the subspace Open problem: how to choose projection? n PCA? 16

Finding a basis for each subspace n Case of hyperplanes: n n There is only one polynomial Basis are normal vectors Polynomial Factorization Alg. (PFA) [CVPR 2003] n n n Find roots of polynomial of degree in one variable Solve linear systems in variables Solution obtained in closed form for n Problems n n n Computing roots may be sensitive to noise The estimated polynomial may not perfectly factor with noisy Cannot be applied to subspaces of different dimensions n Polynomials are estimated up to change basis, hence they may not factor, with perfect data of even 18

Finding a basis for each subspace Theorem: GPCA by differentiation n To learn a mixture of subspaces we just need one positive example per class 20

Choosing points by polynomial division n n With noise and outliers n Polynomials may not be a perfect union of subspaces n Normals can estimated correctly by choosing points optimally Distance to closest subspace without knowing segmentation? 21

GPCA: subspaces of different dimensions n n n There are multiple polynomials fitting the data The derivative of each polynomial gives a different normal vector Can obtain a basis for the subspace by applying PCA to normal vectors 22

GPCA: Algorithm summary n Apply polynomial embedding to projected data n Obtain multiple subspace model by polynomial fitting n n Solve to obtain Need to know number of subspaces n Obtain bases & dimensions by polynomial differentiation n Optimally choose one point per subspace using distance 23

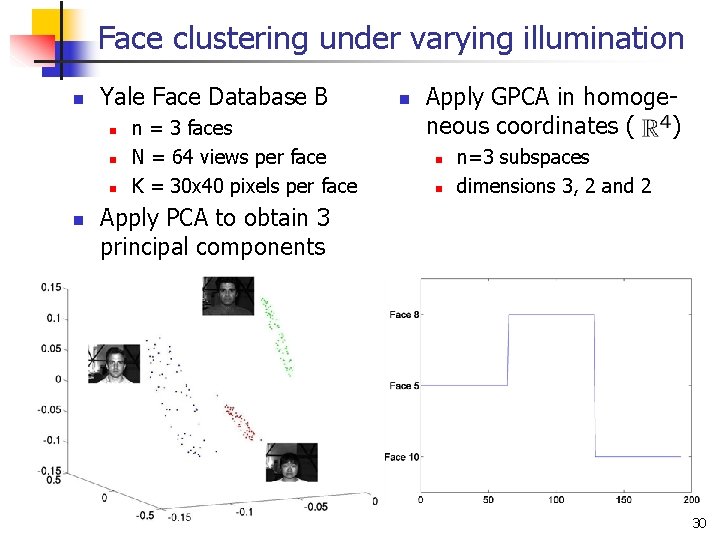
Face clustering under varying illumination n Yale Face Database B n n n = 3 faces N = 64 views per face K = 30 x 40 pixels per face n Apply GPCA in homogeneous coordinates ( ) n n n=3 subspaces dimensions 3, 2 and 2 Apply PCA to obtain 3 principal components 30

News video segmentation n Segmenting N=30 frames of a sequence containing n=3 scenes n n n Host Guest Both n Image intensities are output of linear system images n xt + 1 = Axdynamics t + vt yt = Cxt + wt appearance Apply GPCA to fit n=3 observability subspaces 31

News video segmentation n Segmenting N=60 frames of a sequence containing n=3 scenes n n n Burning wheel Burnt car with people Burning car n Image intensities are output of linear system images n xt + 1 = Axdynamics t + vt yt = Cxt + wt appearance Apply GPCA to fit n=3 observability subspaces 32

3 -D motion segmentation problem n Given a set of point correspondences in multiple views, determine n n Number of motion models Motion models: affine, projective, fundamental matrices, etc. Segmentation: model to which each pixel belongs Mathematics of the problem depends on n n Number of frames (2, 3, multiple) Projection model (affine, perspective) Motion model (affine, translational, planar motion, rigid motion) 3 -D structure (planar or not) 39

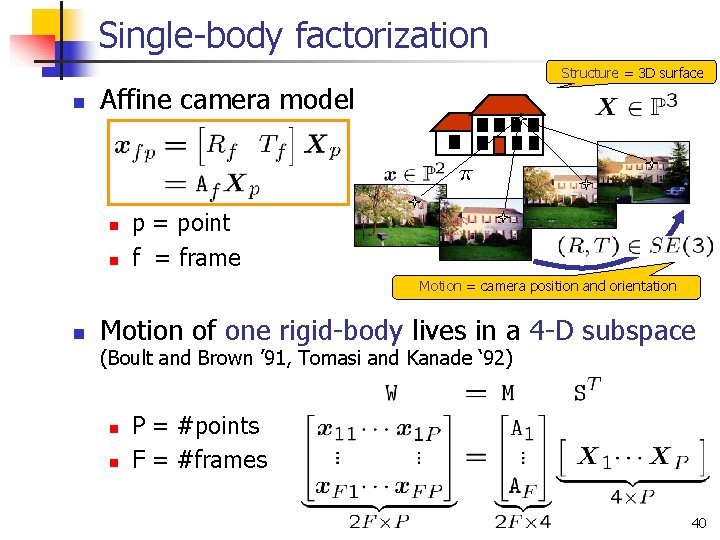
Single-body factorization Structure = 3 D surface n Affine camera model n n p = point f = frame Motion = camera position and orientation n Motion of one rigid-body lives in a 4 -D subspace (Boult and Brown ’ 91, Tomasi and Kanade ‘ 92) n n P = #points F = #frames 40

Multiframe 3 -D motion segmentation n Sequence A Sequence B Sequence C n Percentage of correct classification 42

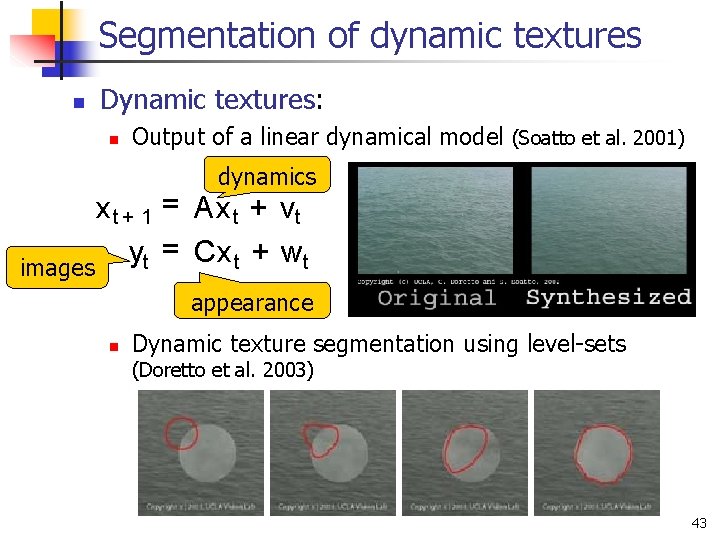
Segmentation of dynamic textures n Dynamic textures: n Output of a linear dynamical model (Soatto et al. 2001) dynamics x t + 1 = Ax t + vt = Cx t + wt y t images appearance n Dynamic texture segmentation using level-sets (Doretto et al. 2003) 43

Segmentation of dynamic textures n One dynamic texture lives in the observability subspace images n Multiple textures live in multiple subspaces n n Apply PCA to image intensities Apply GPCA to projected data 44

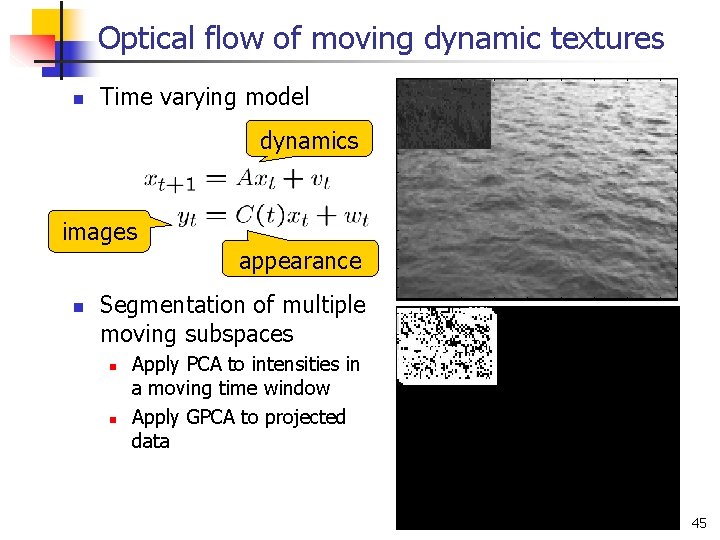
Optical flow of moving dynamic textures n Time varying model dynamics images appearance n Segmentation of multiple moving subspaces n n Apply PCA to intensities in a moving time window Apply GPCA to projected data 45

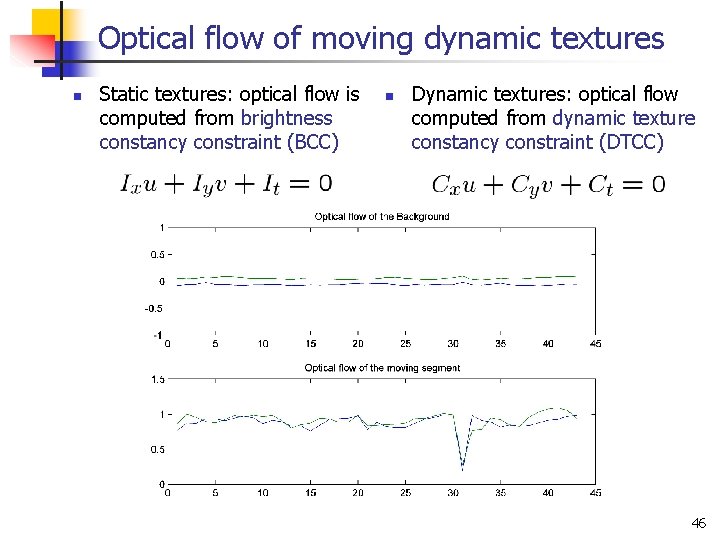
Optical flow of moving dynamic textures n Static textures: optical flow is computed from brightness constancy constraint (BCC) n Dynamic textures: optical flow computed from dynamic texture constancy constraint (DTCC) 46

Conclusions and ongoing work n Algebraic/geometric approach to simultaneous model estimation and data segmentation for n n n Solution based on n Fitting and differentiating polynomials Solution is closed form if nsubspaces ≤ 4 Applications n n n Mixtures of subspaces: linear constraints Mixtures of surfaces: bilinear/trilinear Computer vision: representation, segmentation, recognition Hybrid systems: identification A geometric/statistical theory of segmentation? n n Model selection + robust statistics + GPCA (CVPR’ 04) Connections with spectral clustering and Kernel PCA 50

Thanks to colaborators n University of Illinois n n n Yi Ma Kun Huang Johns Hopkins University n n Australian National University n n Jacopo Piazzi UCLA n n Richard Hartley Stefano Soatto UC Berkeley n Shankar Sastry 51

Texture-based image segmentation GPCA Human 52

Texture-based image segmentation 53

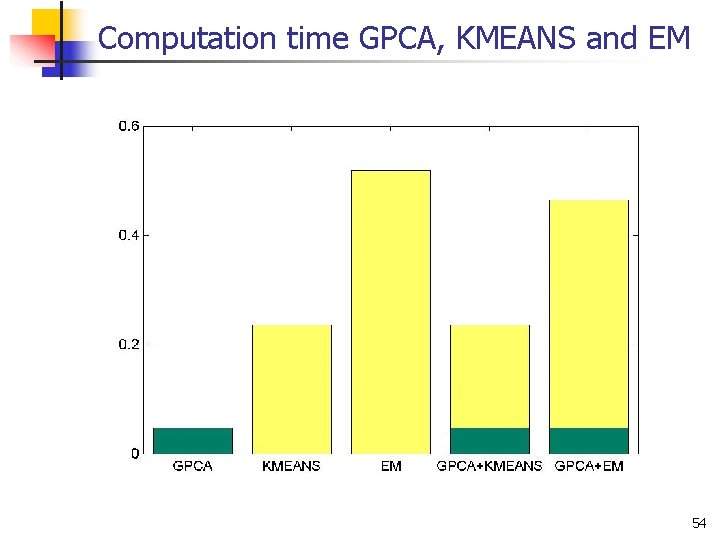
Computation time GPCA, KMEANS and EM 54