Generalized Monte Carlo Tool for Investigating LowField and

Generalized Monte Carlo Tool for Investigating Low-Field and High Field Properties of Materials Using Non-parabolic Band Structure Model Raghuraj Hathwar Advisor : Dr. Dragica Vasileska Computational Electronics

Outline • Motivation of modeling different materials - Strained Silicon - III-V and II-VI materials - Silicon Carbide • The generalized Monte Carlo code - Free-Flight and drift velocity calculation • Rappture interfacing • Results • Conclusions and future work. Computational Electronics

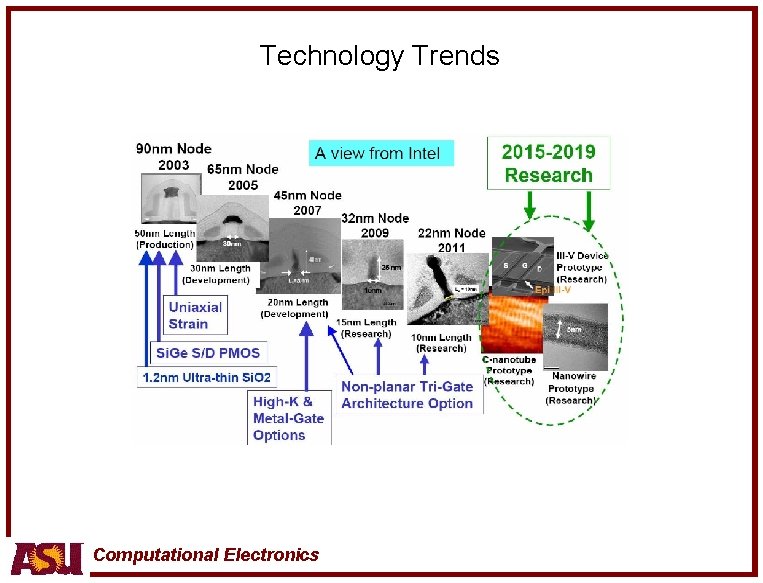
Technology Trends Computational Electronics

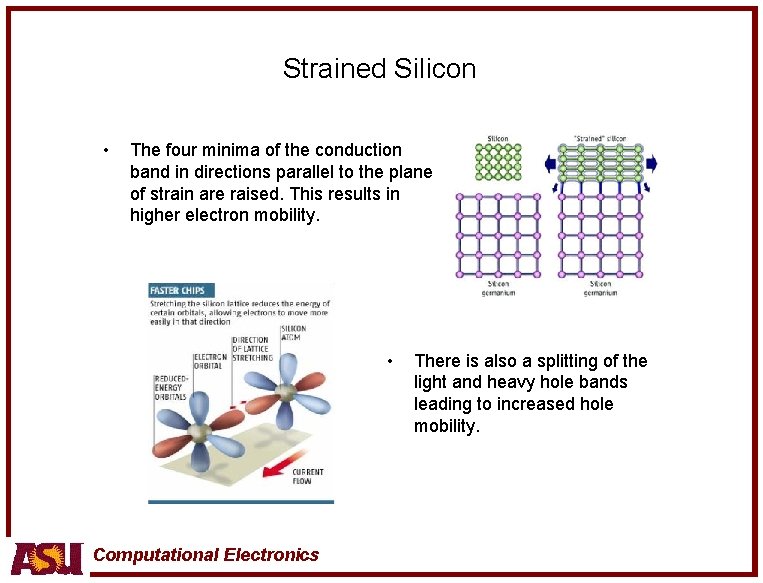
Strained Silicon • The four minima of the conduction band in directions parallel to the plane of strain are raised. This results in higher electron mobility. • Computational Electronics There is also a splitting of the light and heavy hole bands leading to increased hole mobility.

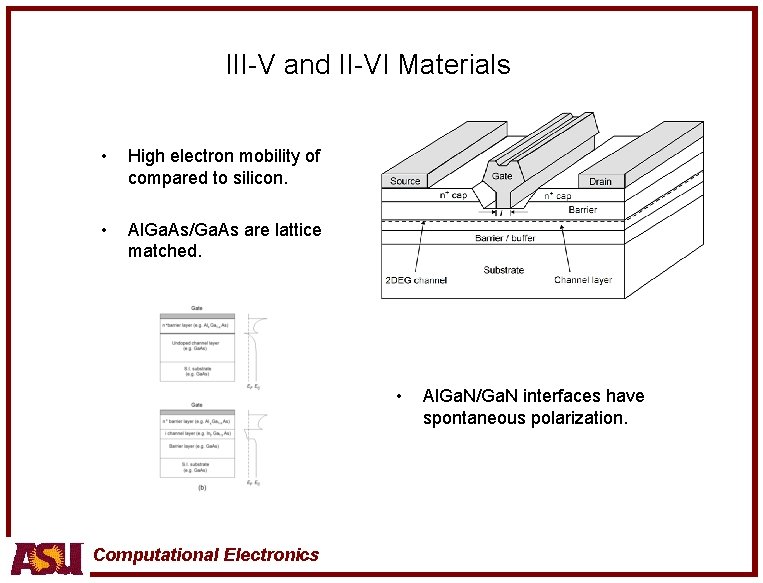
III-V and II-VI Materials • High electron mobility of compared to silicon. • Al. Ga. As/Ga. As are lattice matched. • Computational Electronics Al. Ga. N/Ga. N interfaces have spontaneous polarization.

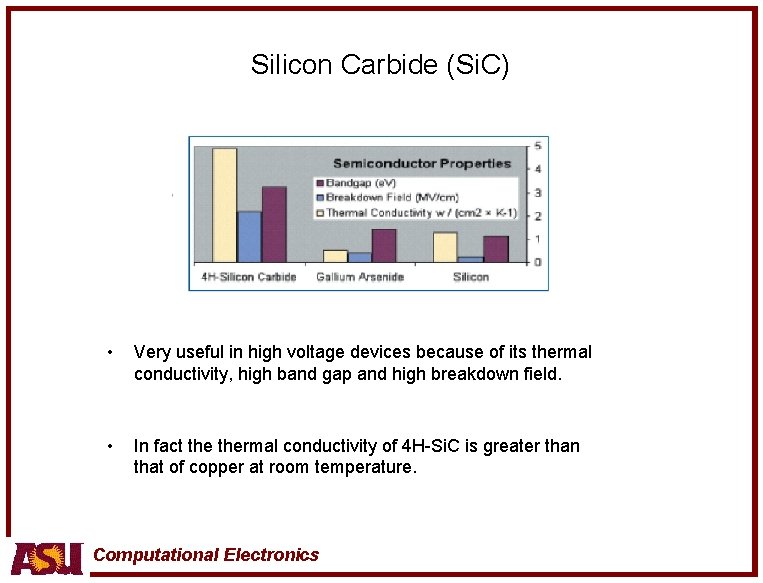
Silicon Carbide (Si. C) • Very useful in high voltage devices because of its thermal conductivity, high band gap and high breakdown field. • In fact thermal conductivity of 4 H-Si. C is greater than that of copper at room temperature. Computational Electronics

The Monte Carlo Method • The Boltzmann Transport Equation • The Chamber-Rees Path Integral Computational Electronics

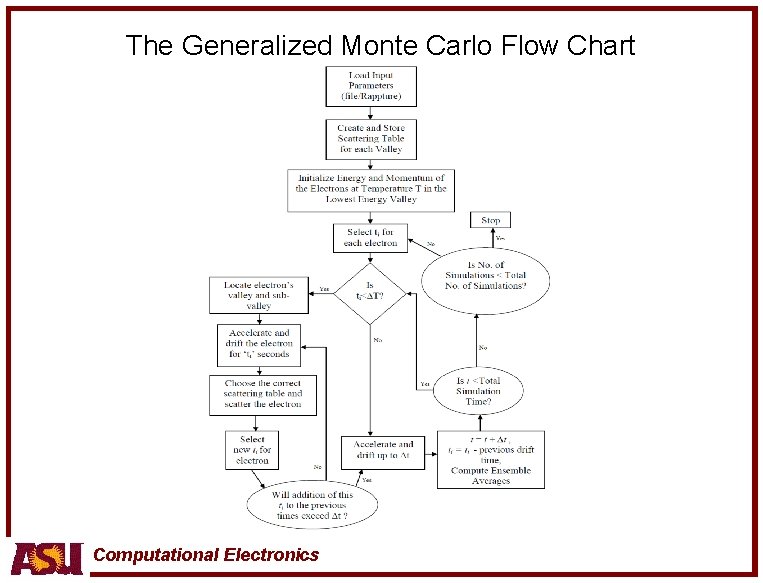
The Generalized Monte Carlo Flow Chart Computational Electronics

Types of Scattering • • • Acoustic Phonon Scattering Zeroth order Intervalley Scattering First order Intervalley Scattering Piezoelectric Scattering Polar Optical Phonon Scattering Ionized Impurity Scattering Computational Electronics

Fermi’s Golden Rule and Scattering Rates Calculation • Calculate the Matrix Element • Use Fermi’s Golden Rule • Sum over all k’ states Computational Electronics

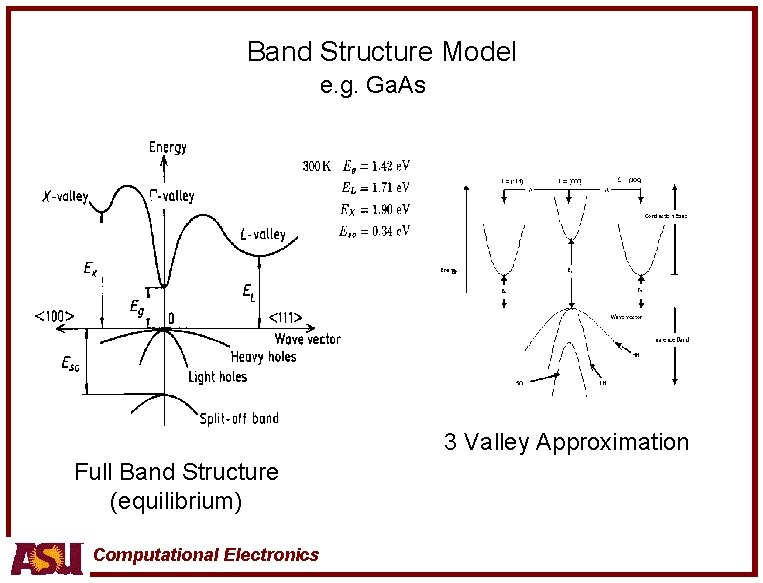
Band Structure Model e. g. Ga. As 3 Valley Approximation Full Band Structure (equilibrium) Computational Electronics

E-k relation for a General Valley Here k 1 , k 2 and k 3 are the wave vectors along the three mutually perpendicular directions that define the valley and m 1 , m 2 and m 3 are the effective masses of the electrons along those directions Computational Electronics

Conversion from Anisotropic Bands to Isotropic Bands In order to make the conversion between energy and momentum easy all anisotropic bands are converted to isotropic bands using Which gives the following E-k relation where Computational Electronics

Carrier Free-Flight From Newton’s 2 nd law and Q. M. Computational Electronics

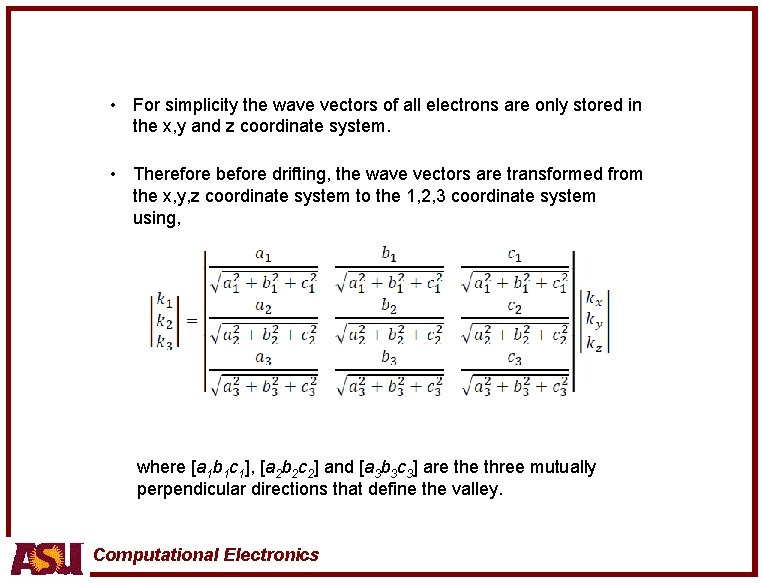
• For simplicity the wave vectors of all electrons are only stored in the x, y and z coordinate system. • Therefore before drifting, the wave vectors are transformed from the x, y, z coordinate system to the 1, 2, 3 coordinate system using, where [a 1 b 1 c 1], [a 2 b 2 c 2] and [a 3 b 3 c 3] are three mutually perpendicular directions that define the valley. Computational Electronics

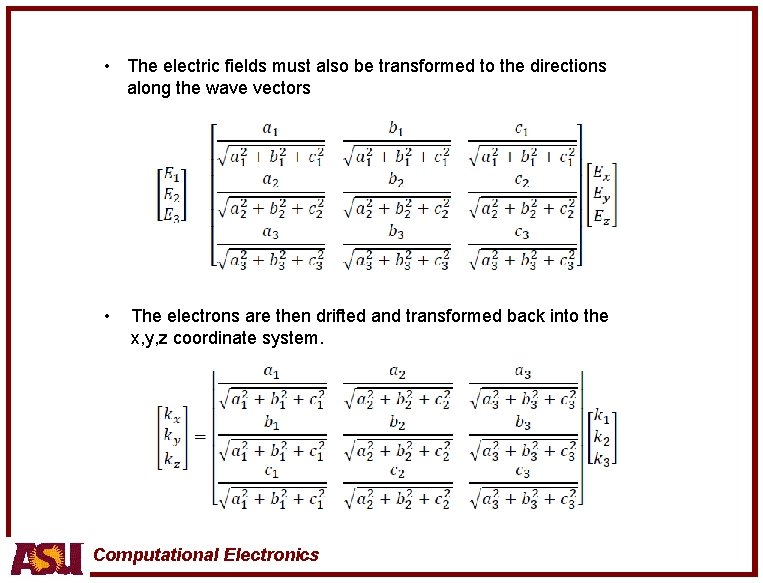
• The electric fields must also be transformed to the directions along the wave vectors • The electrons are then drifted and transformed back into the x, y, z coordinate system. Computational Electronics

Drift Velocity Calculation Computational Electronics

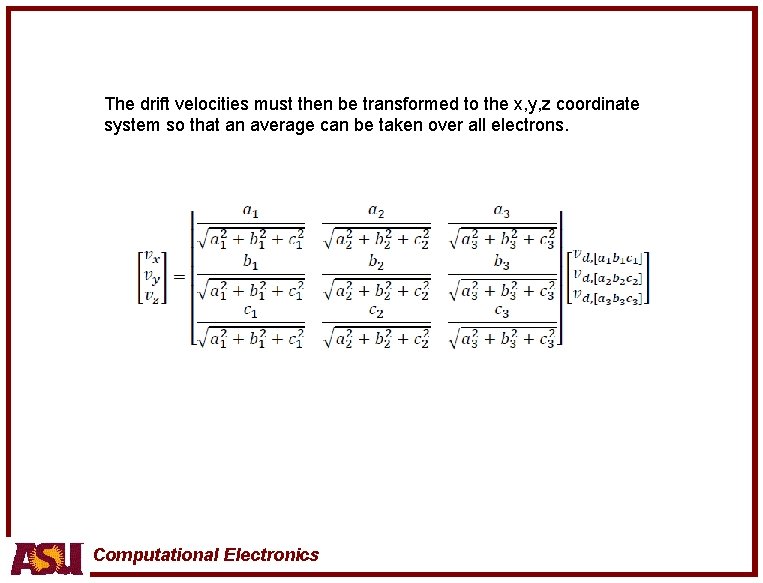
The drift velocities must then be transformed to the x, y, z coordinate system so that an average can be taken over all electrons. Computational Electronics

Rappture Integration • The Rappture toolkit provides the basic infrastructure for a large class of scientific applications, letting scientists focus on their core algorithm when developing new simulators. • Instead of inventing your own input/output, you declare the parameters associated with your tool by describing Rappture objects in the Extensible Markup Language (XML). • Create an xml file describing the input structure. • Integrate the source code with Rappture to read input values and to output results to the Rappture GUI. Computational Electronics

Material Parameters and Simulation Parameters Computational Electronics

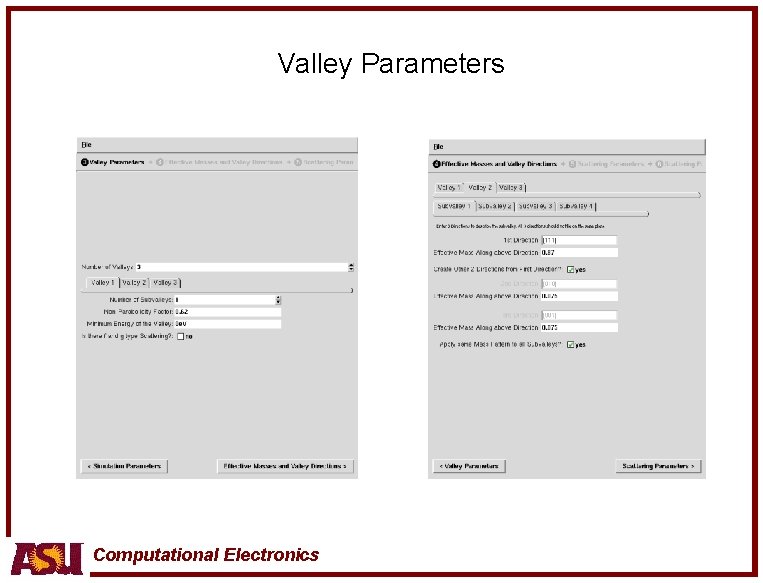
Valley Parameters Computational Electronics

Scattering Parameters Computational Electronics

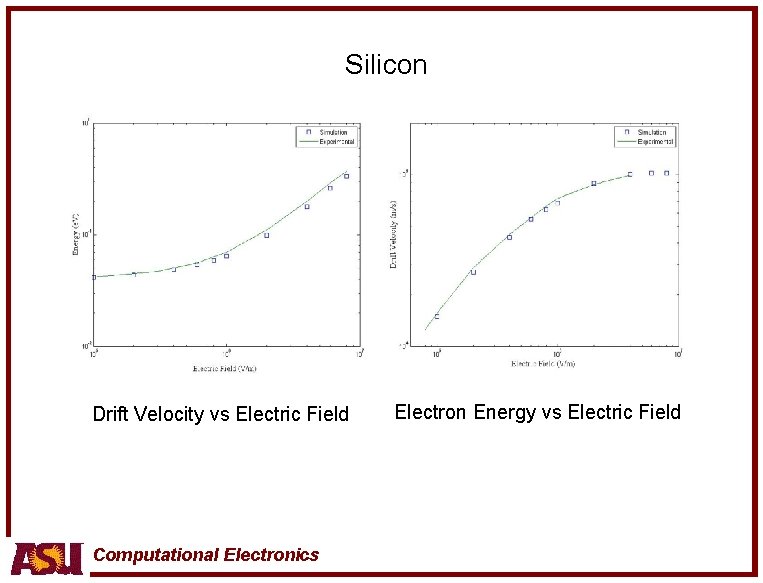
Silicon Drift Velocity vs Electric Field Computational Electronics Electron Energy vs Electric Field

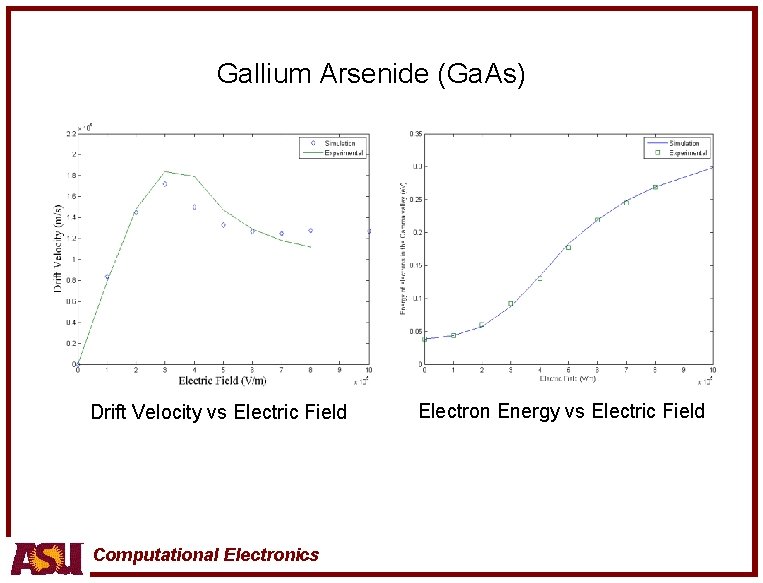
Gallium Arsenide (Ga. As) Drift Velocity vs Electric Field Computational Electronics Electron Energy vs Electric Field

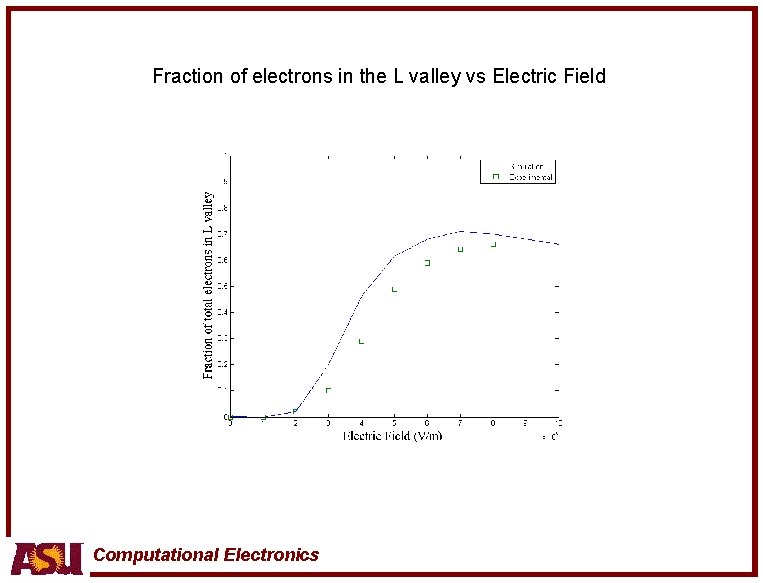
Fraction of electrons in the L valley vs Electric Field Computational Electronics

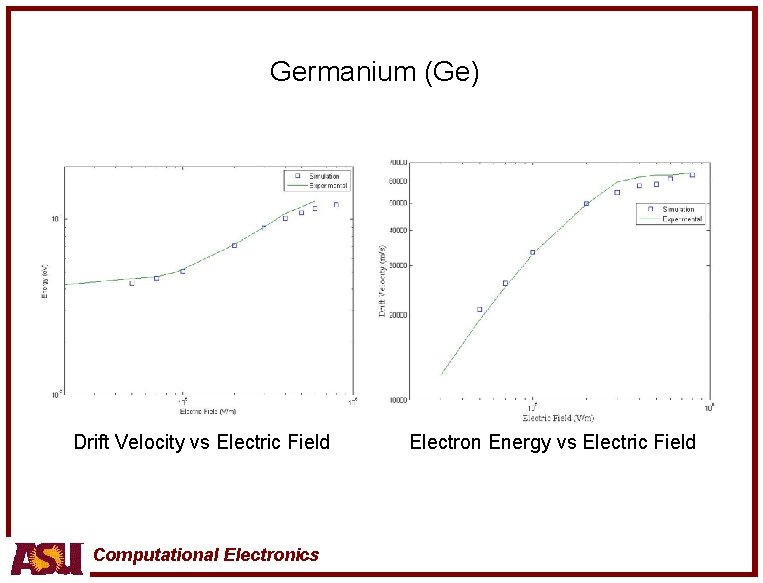
Germanium (Ge) Drift Velocity vs Electric Field Computational Electronics Electron Energy vs Electric Field

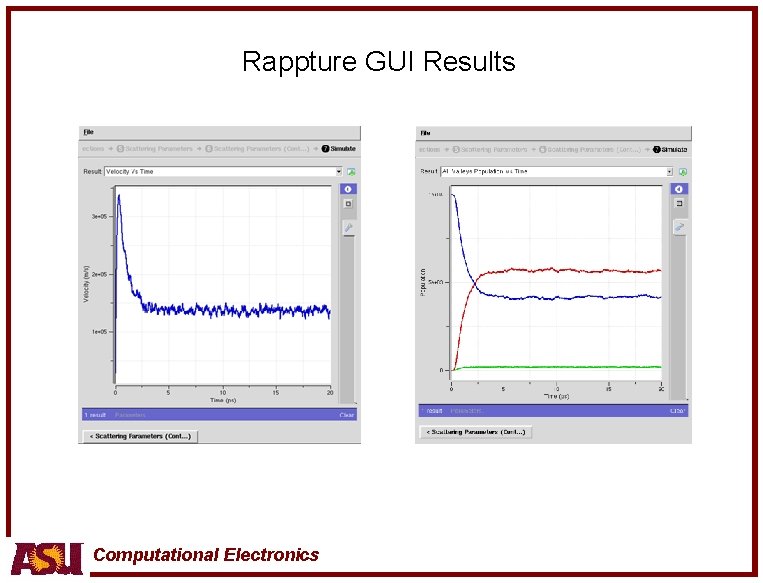
Rappture GUI Results Computational Electronics

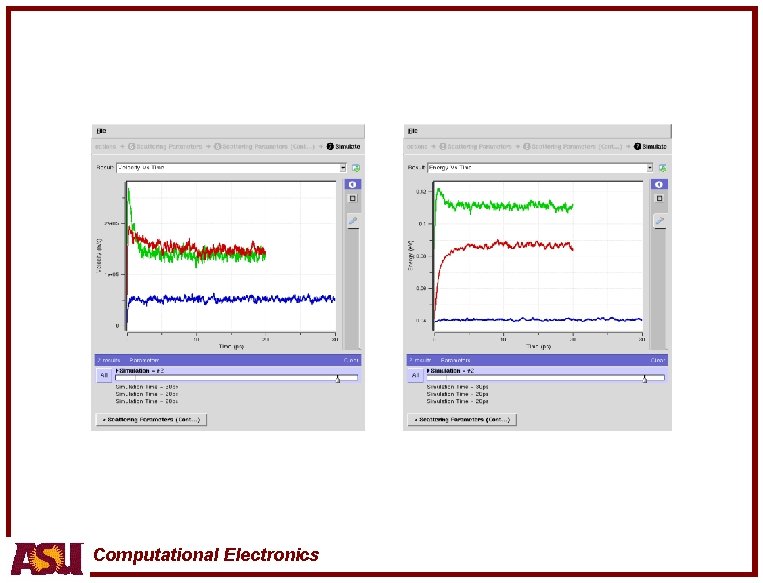
Computational Electronics

Conclusions and Future Work • Uses non-parabolic band structure making it as accurate as possible for an analytic representation of the band structure. • Interfacing the tool with Rappture enables easy handling of the parameters and reduces the complexity of using the tool. • Existing materials band structures can be easily modified to improve existing results. • New materials can easily be added to the code. • The tool can be extended to include impact ionization scattering to better model high field properties. • Full band simulation for holes. Computational Electronics