Generalized Linear Models All the regression models treated


























- Slides: 27

Generalized Linear Models • All the regression models treated so far have common structure. This structure can be split up into two parts: ü The random part: ü The systematic part: • These two elements are the basic building blocks of generalized linear models.

The systematic part • Generalized linear model, systematic part: ü The covariates influence the distribution of response through the linear predictor: ü There is a link-function that links the expectation to the linear predictor:

The generalization from linear models to GLM • GLMs are a generalization of linear normal models in two directions:

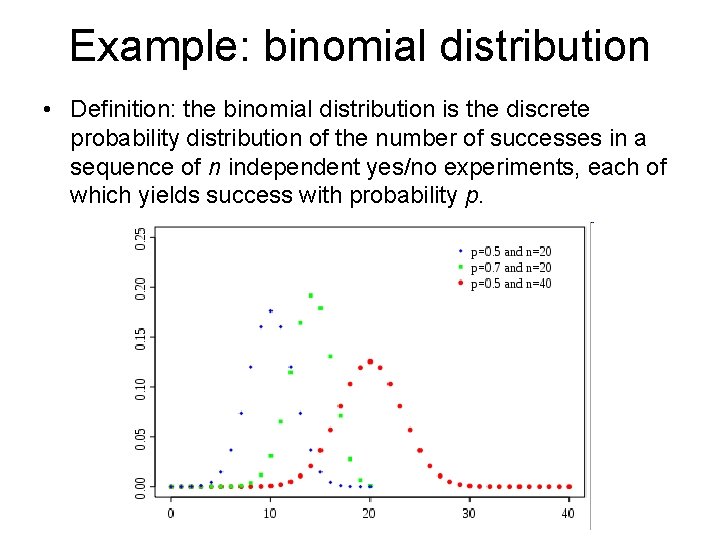
Example: binomial distribution • Definition: the binomial distribution is the discrete probability distribution of the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p.

Example • For the binomial distribution • The variance is a function of the mean: • The linear model for the logit: __________ is a non-linear model for the probability __________.

The exponential family • Many distributions encountered in practice (ex: normal, binomial, Poisson and Gamma distribution) share a common structure:

Example of the exponential family: Normal distribution

Example of the exponential family: Binomial

Example of the exponential family • The Poisson distribution: It is a discrete probability distribution that expresses the probability of a number of events occurring in a fixed period of time if these events occur with a known average rate and independently to the time. • Ex: ü The number of phone calls received by a telephone operator in a 10 -minute period. ü The number of typos per page made by a secretary.

Poisson distribution • The Poisson distribution belongs to the exponential family:

Mean and variance in the exponential family • It can be shown that the mean and variance in the exponential family is:

Mean and variance example: Poisson • For the Poisson model, mean and variance are: • To summarize, for any given distribution we obtain a specific form of b which in turn determines the variance function. • The converse is also true: • Hence specifying a distribution and a variance function is two sides of the same coin as long as we work with exponential families.

Various variance functions

The link function • The link function is a function which relates the mean to the linear predictor: • Various link functions have been illustrated so far:

Canonical link • For each distribution there is a specific link function which yields “nice” mathematical and numerical properties in connection with the estimation process. This link function is called the canonical link:

Specification of GLM • In practice, a GLM is specified by three steps: • In this connection it is important to be aware of the following: Most statistical packages will by default use the canonical link function unless another one is explicitly provided.

R code • The glm function in R is used for fitting generalized linear models. • Specification of the linear predictor: • Specification of the distribution and the link function: e. g. family=Gamma(link=log)

• Remember that the specification of a distribution yields a specific variance function. Not all possible combinations of a distribution and a link function are allowed in R.

Special aspects for binomial data • Simulate artificial Bernoulli observations with different event probabilities for two groups (the number of trails N is equal to 1): R code group <- rep(c("A", "B"), c(30, 45)) logit. pi <- ifelse(group == "B", 0. 7 + 0. 5) group <- factor(group) pi <- plogis(logit. pi) N <- rep(1, length(group)) events <- rbinom(length(group), size = N, prob = pi) dat <- data. frame(group, N, events)

Analysis of simulated data • Model: __________________ • The response is a two-column matrix containing events and nonevents: f 1<-glm(cbind(events, N-events)~group, family=binomial, data=dat) • Define proportions: dat$prop<-with(dat, events/N) and use these as the response and the number of trails N as weights in the fit: f 2<-glm(prop~group, family=binomial, weights=N, data=dat) • Use the number of events directly as the response f 3<-glm(events~group, family=binomial, data=dat)

Fitting GLMs– logistic regression • Consider a data set where the response variable takes only 0 or 1 values and the single covariate variable is continues numerical type. Examples • If we apply a simple linear regression model_____ to fit the data, there are some problems. • Conclusion: it is not appropriate to use the simple linear regression to model regression data with binary responses.

Logistic regression • Solution is to use the logistic function: • The formal definition of logistic model for binary response with p variable:

Logistic regression • How to interpret the model? • In logistic model, the odds of “success”: • The logistic model for binary data can be slightly modified

Modified to cover binomial data

Bernoulli and Poisson distribution • Likelihood: • MLE estimates:

Parameter estimation in GLMs

IWLS Algorithm • Iterative weighted least square algorithm:
 Simple linear regression and multiple regression
Simple linear regression and multiple regression Logistic regression vs linear regression
Logistic regression vs linear regression Logistic regression vs linear regression
Logistic regression vs linear regression Multiple regression formula
Multiple regression formula Linear phase system
Linear phase system Sas generalized linear model
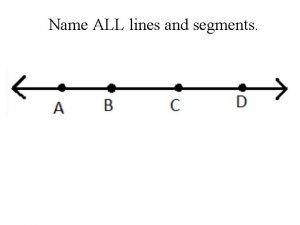
Sas generalized linear model Name all the rays
Name all the rays Semi log functional form
Semi log functional form Qualitative response regression models
Qualitative response regression models Logit model
Logit model Advanced regression and multilevel models
Advanced regression and multilevel models Panel data
Panel data Advanced regression models
Advanced regression models Types of regression models
Types of regression models Knn linear regression
Knn linear regression Hierarchical multiple regression spss
Hierarchical multiple regression spss Linear regression riddle b
Linear regression riddle b Scala meter
Scala meter Multiple linear regression model
Multiple linear regression model Rumus regresi linear sederhana
Rumus regresi linear sederhana Multivariate regression spss
Multivariate regression spss Cost function andrew ng
Cost function andrew ng Linear regression multiple features
Linear regression multiple features Sum of squares
Sum of squares Ap statistics linear regression
Ap statistics linear regression Example of regression analysis
Example of regression analysis Log linear regression model
Log linear regression model F test statistic formula
F test statistic formula