Generalizability Theory EPSY 8224 Classical Test Theory Characteristics

Generalizability Theory EPSY 8224

Classical Test Theory • Characteristics of classical test theory

Generalizability Theory • G-Theory makes no assumptions regarding parallel measurements • Generalizability Coefficient – classic relative-reliability • Dependability Coefficient – absolute reliability

G-Theory Framework • Universe of Admissible Observations • Object of Measurement • Universe of Generalization • Universe Score • Facets • G-study • D-study • Random/Fixed facets • Crossed/Nested designs

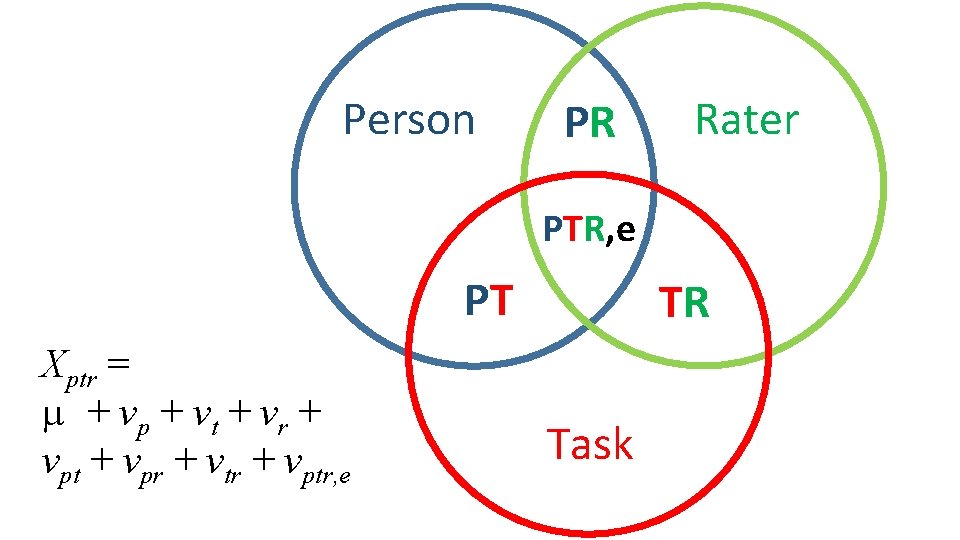
Person PR Rater PTR, e PT Xptr = + vp + vt + vr + vpt + vpr + vtr + vptr, e TR Task

Random-Effects Variance Components 2(Xptr) = 2(p) + 2(t) + 2(r) + 2(pt) + 2(pr) + 2(tr) + 2(ptr, e)

Relative Error Variance • difference between person’s observed deviation score and universe deviation score; • p = (Xp. TR - TR) – ( p - ) • sum of error variance components including p; • square root is the relative SEM, as in CTT

Absolute Error Variance • the difference between a person’s observed score and universe score; • p = Xp. TR - p • the sum of all error variances, not the universe score variance; • the square root is the absolute SEM

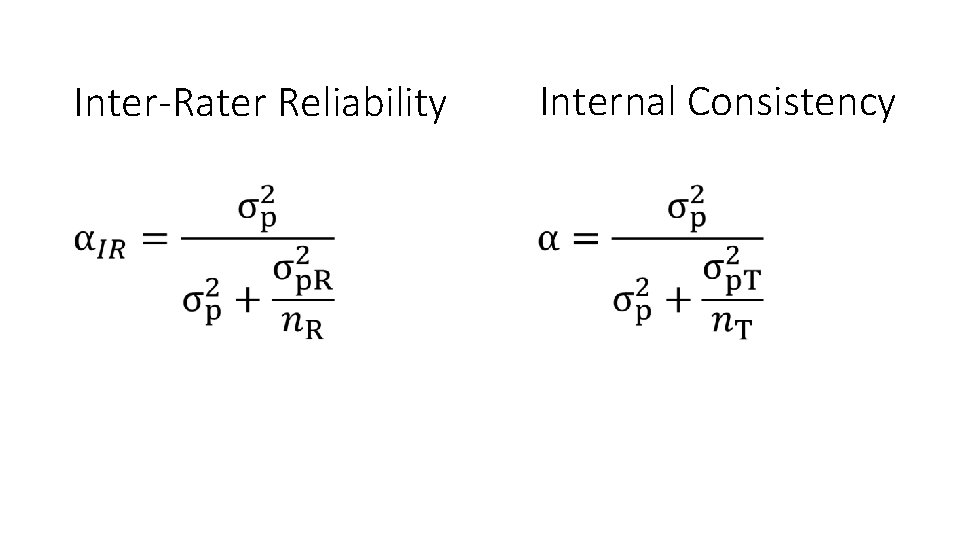
G-Coefficient D-Coefficient • Norm-referenced decisions • Criterion-reference decisions

Inter-Rater Reliability Internal Consistency

G-Study Design Issues • specify as many facets as possible based on major sources of error most likely present in a measurement procedure • use as many crossed facets as possible --- avoid the nested design • if fixed facets are used and the conditions of those facets are not exchangeable, we should do separate G-studies for each condition

G-Study Limitations • assumptions are hard to achieve, including defining the universe and randomly sampling from that universe • sample dependent; dealing with observed scores • doesn’t provide information regarding specific conditions of a given facet (items, persons) • assumes the conditions are exchangeable--ignores maturation within a facet • defining universe of generalization • technical problems: dealing with missing data, dealing with ordered facets

Generalizability Theory of Performance Assessment Brennan, R. L. (1996). Generalizability of performance assessment. In G. W. Phillips (Ed. ), Technical issues in large-scale performance assessment. Washington, DC: National Center for Education Statistics, U. S. Department of Education.

California Assessment Program • statewide science assessment in 1989 -1990. • Students were posed five independent tasks. • More specifically, students rotated through a series of five selfcontained stations at timed intervals (about 15 mins. ).

CAP Science Tasks • determine which of the provided materials may serve as a conductor • develop a classification system for leaves and then to explain any adjustments necessary to include a new mystery leaf in the system • conduct tests with rocks and then use the results to determine the identity of an unknown rock • estimate and measure various characteristics of water (e. g. , temperature, volume) • conduct a series of tests on samples of lake water to discover why fish are dying (e. g. , is the water too acidic? )

CAP Scoring • A predetermined scoring rubric developed by teams of teachers in California was used to evaluate the quality of students’ written responses to each of the tasks. • Each rubric was used to score performance on a scale • • • 0 = no attempt 1 = serious flaws 2 = satisfactory 3 = competent 4 = outstanding • All tasks were scored by three raters.

G-Theory Study Framing • Universe of Admissible Observations (facets of the measurement procedures) • Tasks (t) • Raters (r) • txr • Population • Persons (p) • pxtxr

G-Theory Study design • A sample of five tasks were drawn from the UAO, administered to a sample of persons (students), and a sample of three raters evaluated all responses produced by all persons. • pxtxr • Fully crossed, random effects G-study design.

• MBE = multistate bar exam • WK-L & WK-W = Work Keys Listening and Writing (ACT)

An Empirical Example • 30 students • Three raters • Four tasks • All facets are crossed

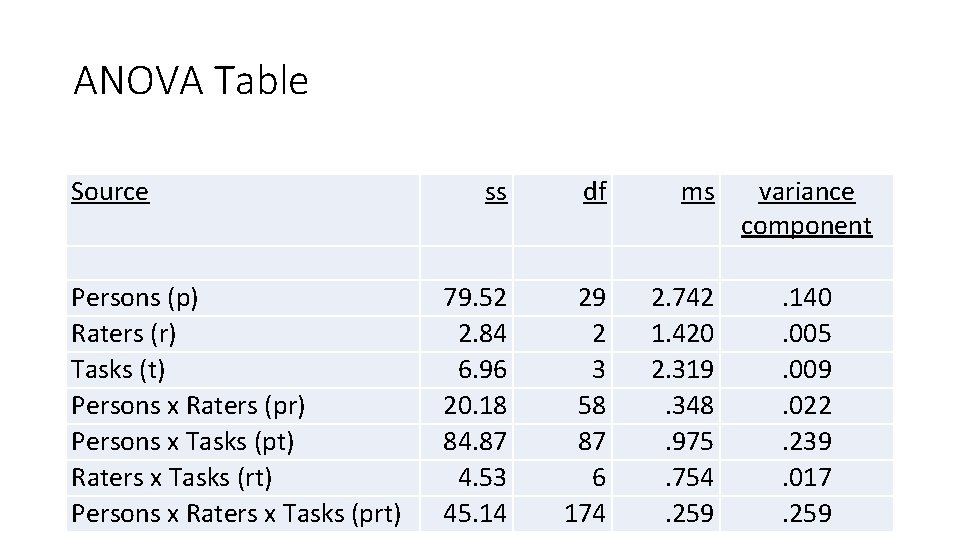
ANOVA Table Source Persons (p) Raters (r) Tasks (t) Persons x Raters (pr) Persons x Tasks (pt) Raters x Tasks (rt) Persons x Raters x Tasks (prt) ss df ms 79. 52 2. 84 6. 96 20. 18 84. 87 4. 53 45. 14 29 2 3 58 87 6 174 2. 742 1. 420 2. 319. 348. 975. 754. 259 variance component. 140. 005. 009. 022. 239. 017. 259

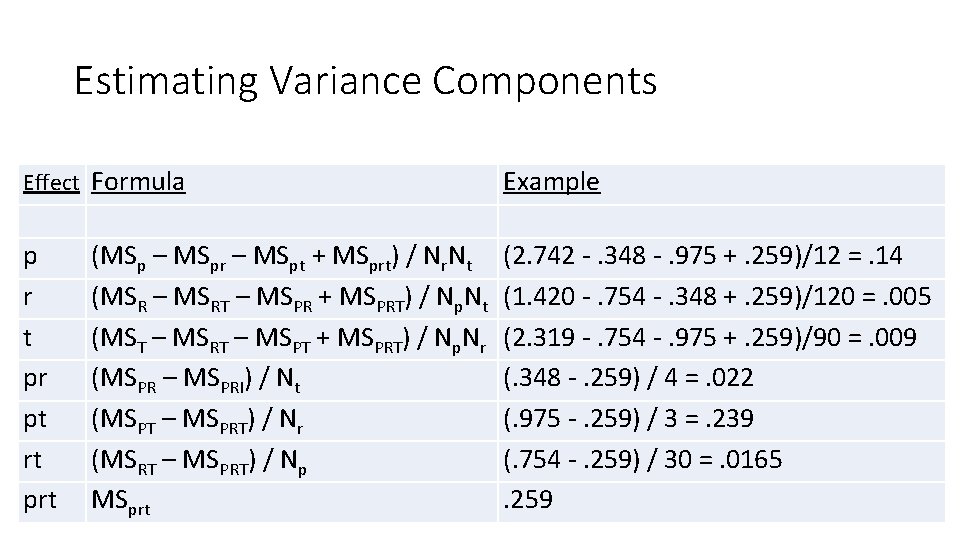
Estimating Variance Components Effect Formula Example p r t pr pt rt prt (2. 742 -. 348 -. 975 +. 259)/12 =. 14 (1. 420 -. 754 -. 348 +. 259)/120 =. 005 (2. 319 -. 754 -. 975 +. 259)/90 =. 009 (. 348 -. 259) / 4 =. 022 (. 975 -. 259) / 3 =. 239 (. 754 -. 259) / 30 =. 0165. 259 (MSp – MSpr – MSpt + MSprt) / Nr. Nt (MSR – MSRT – MSPR + MSPRT) / Np. Nt (MST – MSRT – MSPT + MSPRT) / Np. Nr (MSPR – MSPRI) / Nt (MSPT – MSPRT) / Nr (MSRT – MSPRT) / Np MSprt

Estimating Generalizability • To generalize to a similar measurement procedure as used in the design of the G-Study, we estimate the G-Coefficient as a function of three randomly selected raters and four randomly selected tasks

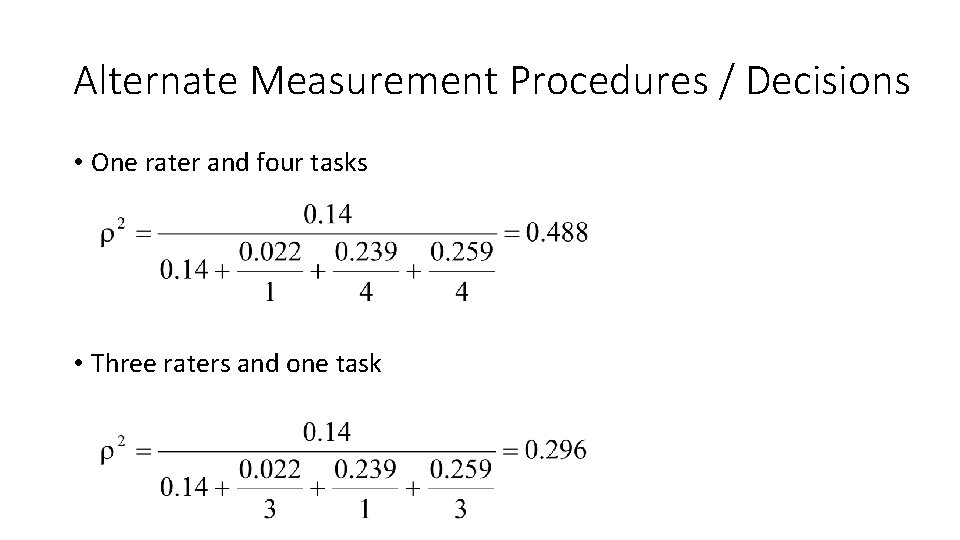
Alternate Measurement Procedures / Decisions • One rater and four tasks • Three raters and one task

Alternate Measurement Procedures / Decisions • Three raters and four tasks where tasks are fixed