Generalisation Fostering Supporting Algebraic Thinking John Mason Trondheim

Generalisation: Fostering & Supporting Algebraic Thinking John Mason Trondheim Oct 2007 1

Assumptions /Generalisation lies at the very core of mathematics and mathematical thinking /A lesson without the opportunity for learners to generalise … is not a mathematics lesson! 2

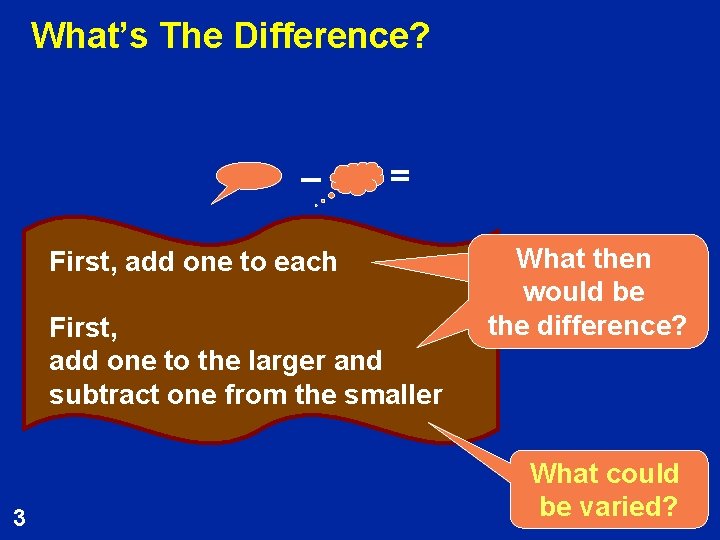
What’s The Difference? – = First, add one to each First, add one to the larger and subtract one from the smaller 3 What then would be the difference? What could be varied?

Think Of A Number (Thoan) intrigues adolescents / Displays power over numbers / Introduces a device for dealing with as-yetunknown numbers / 4

Four Consecutives /Write down four consecutive numbers and add them up /and another /Now be more extreme! /What is the same, and what is different about your answers? 5 +1 +2 +3 4 +6

Powers /Imagining & Expressing /Specialising & Generalising /Conjecturing & Convincing /Classifying & Characterising /Fixing & Changing /Stressing & Ignoring /Attending & Intending 6

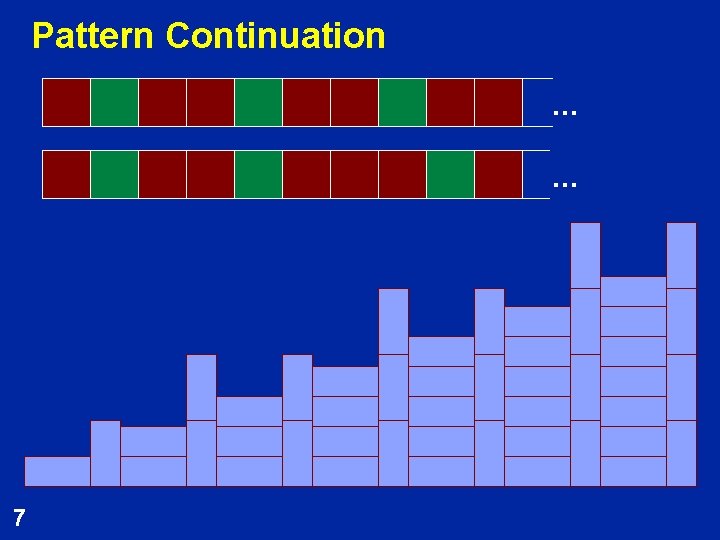
Pattern Continuation … … 7

Experiencing Generalisation /Going with the grain: enactive generalisation /Going across the grain: cognitive generalisation /Pleasure in use of powers; disposition: affective generalisation (Helen Drury) 8

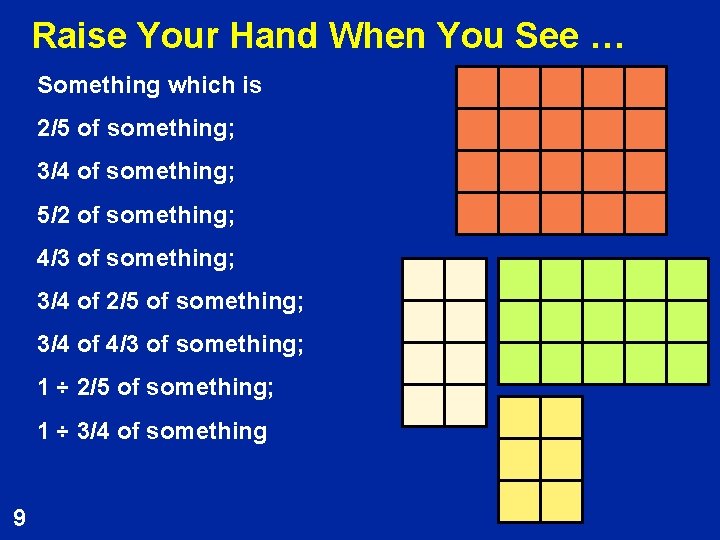
Raise Your Hand When You See … Something which is 2/5 of something; 3/4 of something; 5/2 of something; 4/3 of something; 3/4 of 2/5 of something; 3/4 of 4/3 of something; 1 ÷ 2/5 of something; 1 ÷ 3/4 of something 9

Copper. Plate Multiplication 10

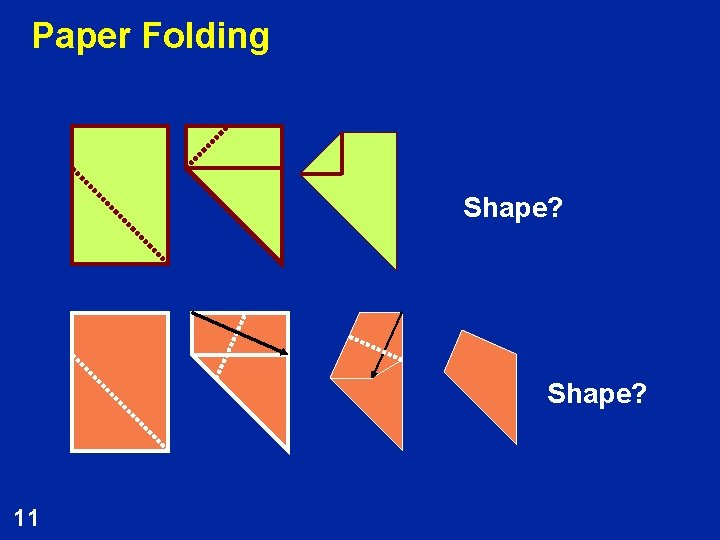
Paper Folding Shape? 11

What Would Happen If …? /The tap wasn’t turned off /It never rained /The power went off /A nearby stream flooded /You kept on cutting a piece of paper in half /… 12

One More What numbers are one more than the sum of four consecutive integers? / What numbers are one more than the product of four consecutive integers? / Let a and b be any two numbers, one of them even. Then ab/2 more than the product of: any number, a more than it, b more than it and a+b more than it, is a perfect square, of the number squared plus a+b times the number plus ab/2 squared. 13

Perforations How many holes for a sheet of r rows and c columns of stamps? 14 If someone claimed there were 228 perforations in a sheet, how could you check?

15

Consecutive Sums Say What You See 16 Say What You See

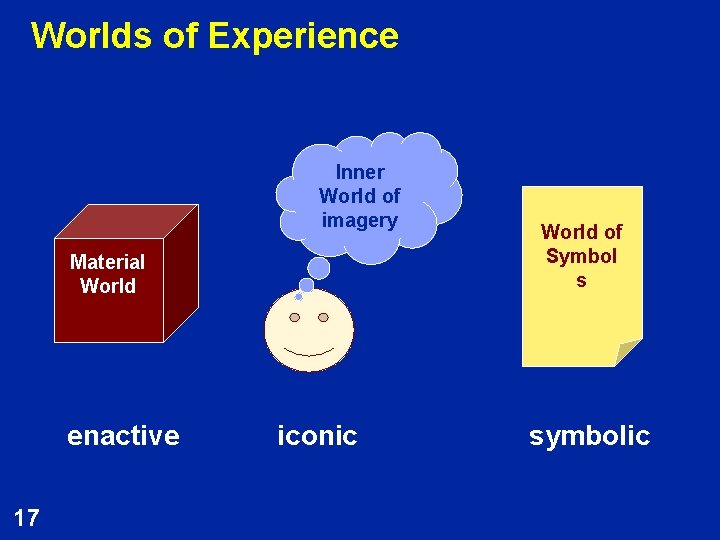
Worlds of Experience Inner World of imagery Material World enactive 17 iconic World of Symbol s symbolic

Remainders of the Day (1) /Write down a number which when you subtract 1 is divisible by 5 /and another /Write down one which you think no-one else here will write down. 18

Remainders of the Day (2) Write down a number which when you subtract 1 is divisible by 2 / and when you subtract 1 from the quotient, the result is divisible by 3 /and when you subtract 1 from that quotient the result is divisible by 4 /Why must any such number be divisible by 3? / 19

Remainders of the Day (3) Write down a number which is 1 more than a multiple of 2 / and which is 2 more than a multiple of 3 / and which is 3 more than a multiple of 4 /… / 20

Remainders of the Day (4) Write down a number which is 1 more than a multiple of 2 / and 1 more than a multiple of 3 / and 1 more than a multiple of 4 /… / 21

Four Odd Sums 22

Slope Reading 23

Cutting Chocolate Bars /In how few cuts can you separate the bar into its pieces? /You can only cut one piece at a time! 24

4 3 4 2 41 4 4 2 1 20 4 5 2 2 7 4 6 2 3 8 4 7 2 4 99 4 0 39 19 6 1 2 18 5 4 3 38 17 16 15 14 37 36 35 34 33 48 2 25 5 1 0 1 1 1 2 1 3 3 2 49 4 9 2 6 2 7 2 8 2 9 3 0 3 1 5 0

64 36 37 38 39 35 14 15 16 34 1 3 1 2 3 1 33 3 2 1 1 3 0 2 9 18 4 2 19 4 3 20 3 4 2 1 2 2 2 3 2 4 4 0 17 41 2 1 0 9 1 5 8 7 6 2 8 2 7 2 6 2 5 4 4 4 5 4 6 4 7 48 4 9 5 0 81