General Linear Model Beatriz Calvo Davina Bristow Overview

General Linear Model Beatriz Calvo Davina Bristow

Overview n n Summary of regression Matrix formulation of multiple regression Introduce GLM Parameter Estimation ¨ Residual n n sum of squares GLM and f. MRI model ¨ Linear Time Series ¨ Design Matrix ¨ Parameter estimation n Summary

Summary of Regression n Linear regression models the linear relationship between a single dependent variable, Y, and a single independent variable, X, using the equation: Y = βX + c + ε n The regression coefficient, β, reflects how much of an effect X has on Y n ε is the error term and is assumed to be independently, identically, and normally distributed (mean 0 and variance σ 2)

Summary of Regression n n Multiple regression is used to determine the effect of a number of independent variables, X 1, X 2, X 3 etc, on a single dependent variable, Y The different X variables are combined in a linear way and each has its own regression coefficient: Y = β 1 X 1 + β 2 X 2 +…. . + βLXL + ε n n The β parameters reflect the independent contribution of each independent variable, X, to the value of the dependent variable, Y. i. e. the amount of variance in Y that is accounted for by each X variable after all the other X variables have been accounted for

Matrix formulation n Multiplying matrices reminder: abc x G H def I = Gxa+Hxb+Ixc Gxd+Hxe+Ixf

Matrix Formulation n Write out equation for each observation of variable Y from 1 to J: Y 1 = X 11β 1 +…+X 1 lβl +…+ X 1 LβL + ε 1 Yj = Xj 1β 1 +…+Xjlβl +…+ Xj. LβL + εj YJ = XJ 1β 1 +…+XJlβl +…+ XJLβL + εJ n. Can turn these simultaneous equations into matrix form to get a single equation: Y 1 Yj YJ Y Observed data = X 11 … X 1 l … X 1 L Xj 1 … X 1 l … X 1 L X 11 … X 1 l … X 1 L β 1 βj βJ + ε 1 εj εJ = X β + ε Design Matrix x Parameters Residuals/Error

General Linear Model n This is simply an extension of multiple regression n Or alternatively Multiple Regression is just a simple form of the General Linear Model n Multiple Regression only looks at ONE dependent (Y) variable n Whereas, GLM allows you to analyse several dependent, Y, variables in a linear combination n i. e. multiple regression is a GLM with only one Y variable n ANOVA, t-test, F-test, etc. are also forms of the GLM

GLM - continued. . n In the GLM the vector Y, of J observations of a single Y variable, becomes a MATRIX, of J observations of N different Y variables n An f. MRI experiment could be modelled with matrix Y of the BOLD signal at N voxels for J scans n However SPM takes a univariate approach, i. e. each voxel is represented by a column vector of J f. MRI signal measurements, and it processed through a GLM separately n (this is why you then need to correct for multiple comparisons)

GLM and f. MRI How does the GLM apply to f. MRI experiments? Y = X . Observed data: Design matrix: SPM uses a mass univariate approach – that is each voxel is treated as a separate column vector of data. Y is the BOLD signal at various time points at a single voxel Several components which explain the observed data, i. e. the BOLD time series for the voxel Timing info: onset vectors, Omj, and duration vectors, Dmj HRF, hm, describes shape of the expected BOLD response over time Other regressors, e. g. realignment parameters β + ε Parameters: Error: Define the contribution of each component of the design matrix to the value of Y Estimated so as to minimise the error, ε, i. e. least sums of squares Difference between the observed data, Y, and that predicted by the model, Xβ�. Not assumed to be spherical in f. MRI

Parameter estimation n In linear regression the parameter β is estimated so that the best prediction of Y can be obtained from X n i. e. sums of squares of difference between predicted values and observed data, (i. e. the residuals, ε) is minimised n Remember last week’s talk & graph! n The method of estimating parameters in GLM is essentially the same, i. e. minimising sums of squares (ordinary least squares), it just looks more complicated

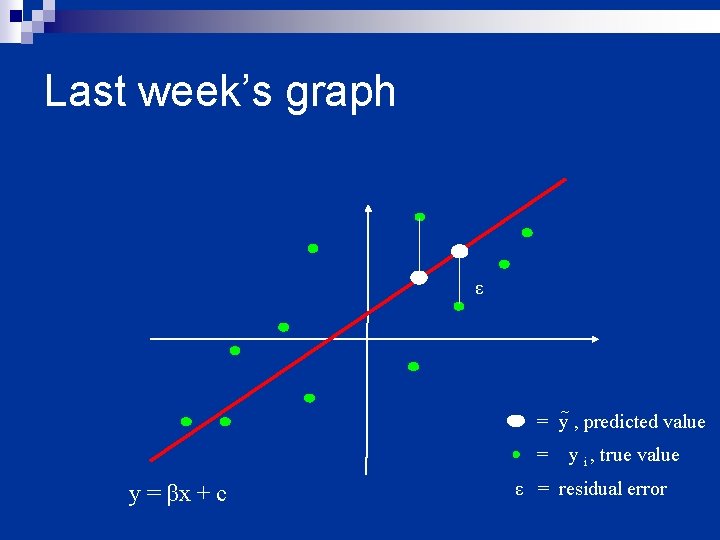
Last week’s graph ε = y , predicted value = y = βx + c y i , true value ε = residual error

Residual Sums of Squares n Take a set of parameter estimates, β� n Put these into the GLM equation to obtain estimates of Y from X, i. e. fitted values, Y�: Y�= X x β� n The residual errors, e, are the difference between the fitted and actual values: e = Y - Y�= Y - Xβ� S = Σj. Jej 2 n Residual sums of squares is: n When written out in full this gives: S = Σj. J(Yj - Xj 1β� 1 -…- Xj. Lβ�L)2

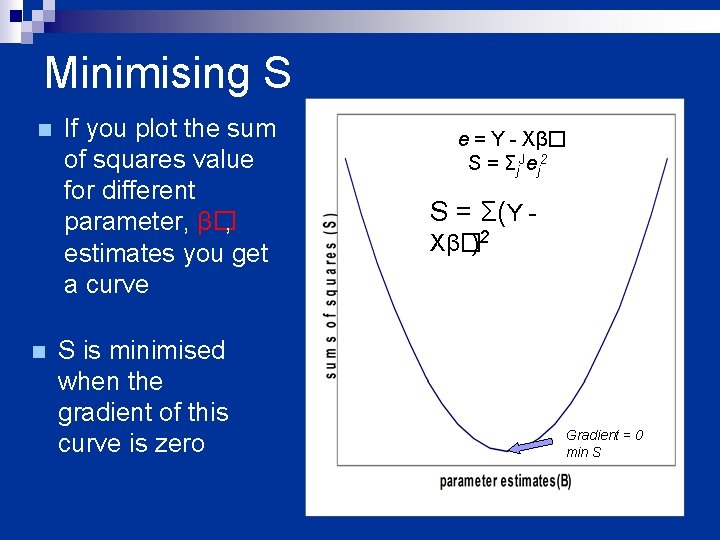
Minimising S n n If you plot the sum of squares value for different parameter, β�, estimates you get a curve S is minimised when the gradient of this curve is zero e = Y - Xβ� S = Σj. Jej 2 S = Σ(Y Xβ�)2 Gradient = 0 min S

Minimising S cont. § so to calculate the values of β�which gives you the least sums of squares you must find the partial derivative of S = Σj. J(Yj - Xj 1β� 1 -…- Xj. Lβ�L)2 § Which is ∂S/∂β�= 2Σ(-Xjl)(Yj – Xj 1β� 1 -…- Xj. Lβ�L) and solve this for ∂S/∂β�= 0 § In matrix form of the residual sum of squares is S = e. T e this is equivalent to Σj. Jej 2 (remember how we multiply matrices) T

Minimising S cont. n Need to find the derivative and solve for ∂S/∂β�= 0 n The derivative of this equation can be rearranged to give XTY = (XTX)β� when the gradient of the curve = 0, i. e. S is minimised n This can be rearranged to give: β�= XTY(XTX)-1 n But a solution can only be found, if (XTX) is invertible because you need to divide by it, which in matrix terms is the same as multiplying by the inverse!

GLM and f. MRI How does the GLM apply to f. MRI experiments? Y = X . Observed data: Design matrix: SPM uses a mass univariate approach – that is each voxel is treated as a separate column vector of data. Y is the BOLD signal at various time points at a single voxel Several components which explain the observed data, i. e. the BOLD time series for the voxel Timing info: onset vectors, Omj, and duration vectors, Dmj HRF, hm, describes shape of the expected BOLD response over time Other regressors, e. g. realignment parameters β + ε Parameters: Error: Define the contribution of each component of the design matrix to the value of Y Estimated so as to minimise the error, ε, i. e. least sums of squares Difference between the observed data, Y, and that predicted by the model, Xβ�. Not assumed to be spherical in f. MRI

f. MRI models n Completed the experiment, after preprocessing, the data are ready for STATS. n STATS: (estimate parameters, β, inference) n indicating evidence against the Ho of no effect at each voxel are computed->an image of this statistic is produce n This statistical image is assessed (other talk will explain that)

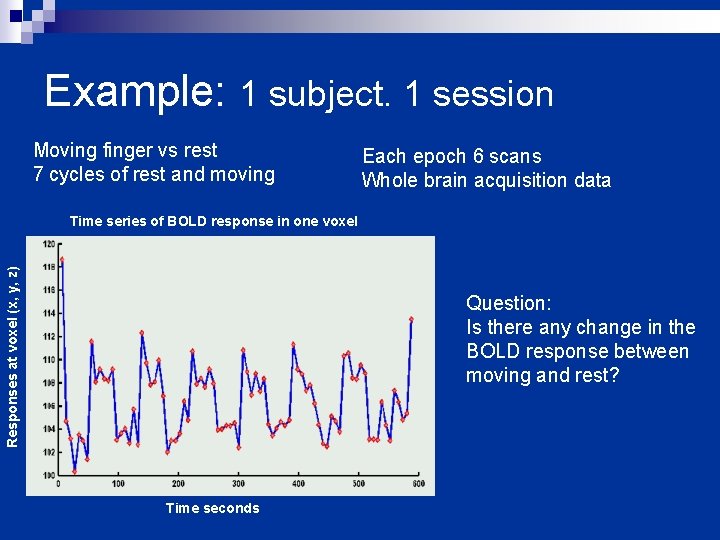
Example: 1 subject. 1 session Moving finger vs rest 7 cycles of rest and moving Each epoch 6 scans Whole brain acquisition data Responses at voxel (x, y, z) Time series of BOLD response in one voxel Question: Is there any change in the BOLD response between moving and rest? Time seconds

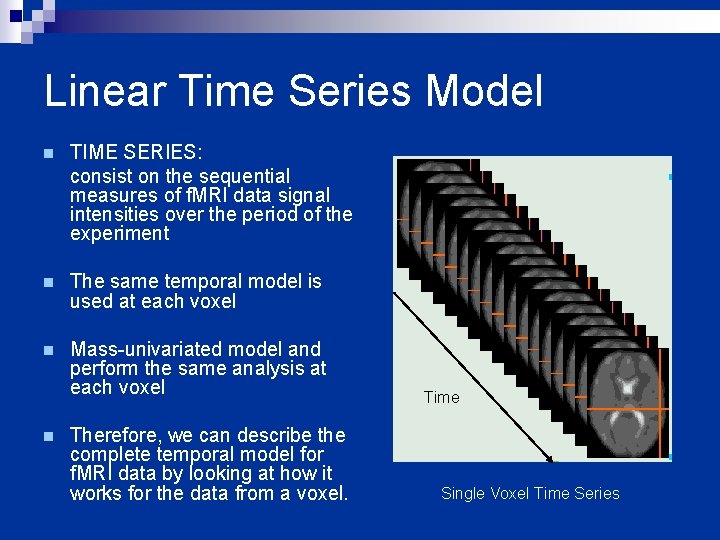
Linear Time Series Model n TIME SERIES: consist on the sequential measures of f. MRI data signal intensities over the period of the experiment n The same temporal model is used at each voxel n Mass-univariated model and perform the same analysis at each voxel n Therefore, we can describe the complete temporal model for f. MRI data by looking at how it works for the data from a voxel. Time Single Voxel Time Series

Y: My data/ observations My Data n Time series of N observations Y 1, …, Ys, …, Yn. N= scan number n Time Single Voxel Time Series Acquired at one voxel at times ts, where S=1: N Y 1 Ys YN

Model specification n The overall aim of regressor generation is to come up with a design matrix that models the expected f. MRI response at any voxel as a linear combinations of columns. n Design matrix – formed of several components which explain the observed data. n Two things SPM need to know to construct the design matrix: n n Specify regressors Basis functions that explain my data

Model specification … n Specify regressors X ¨ Timing information consists of onset vectors Omj and duration vectors Dm ¨ Other regressors e. g. movement parameters ¨ Include as many regressors as you consider necessary to best explain what’s going on. n Basis functions that explain my data (HRF) ¨ Expected shape of the BOLD response due to stimulus presentation

GLM and f. MRI data n Model the observed time series at each voxel as a linear combination of explanatory functions, plus an error term Ys= β 1 X 1(t. S)+ …+ βl Xl(t. S)+ …+ βL XL(t. S) + εs n Here, each column of the design matrix X contains the values of one of the continuous regressors evaluated at each time point ts of f. MRI time series n That is, the columns of the design matrix are the discrete regressors

GLM and f. MRI data … n Consider the equation for all time points, to give a set of equations Y 1= β 1 X 1(t 1)+ …+ βl Xl(t 1)+ …+ βL XL(t 1) + ε 1 Ys= β 1 X 1(t. S)+ …+ βl Xl(t. S)+ …+ βL XL(t. S) + εs YN= β 1 X 1(t. N)+ …+ βl Xl(t. N)+ …+ βL XL(t. N) + εN In matrix form: Y 1 Ys YN In matrix notation: = X 1(t 1) X 1(t. S) X 1(t. N) Xl(t 1) Xl(t. S) Xl(t. N) Y=Xβ+ε XL(t 1) XL(t. S) XL(t. N) β 1 βl βL + εN εs εN

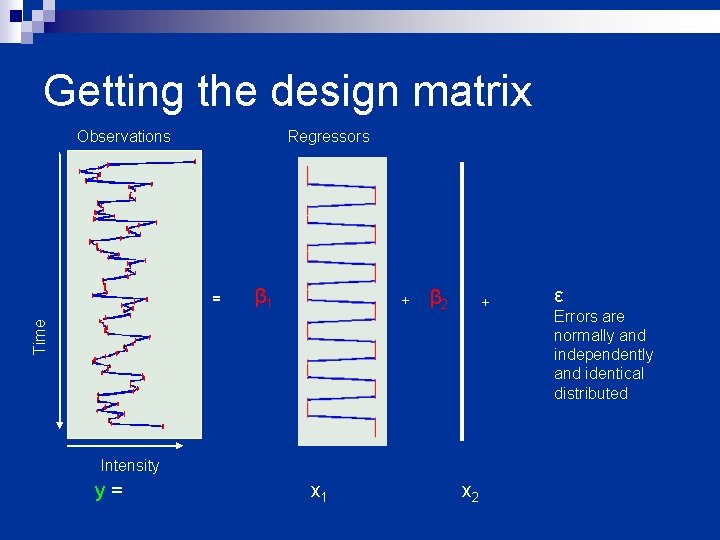
Getting the design matrix Observations Regressors β 1 + β 2 + Time = Intensity y= x 1 x 2 ε Errors are normally and independently and identical distributed

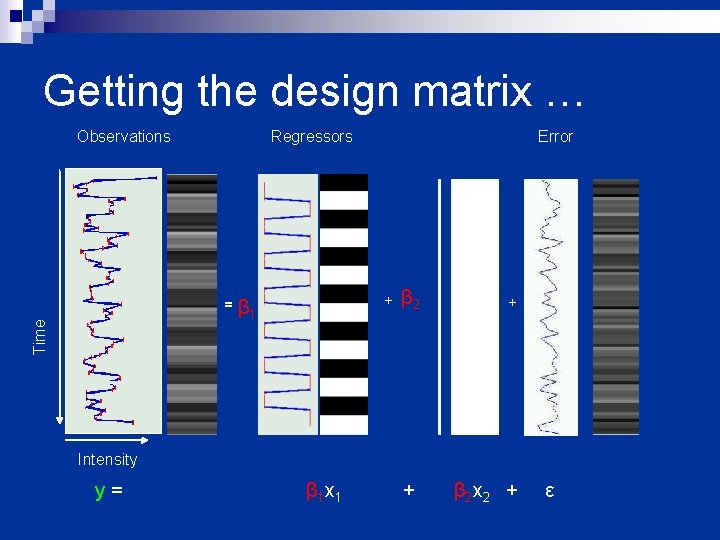
Getting the design matrix … Observations Regressors Time = Error + β 1 β 2 + Intensity y= β 1 x 1 + β 2 x 2 + ε

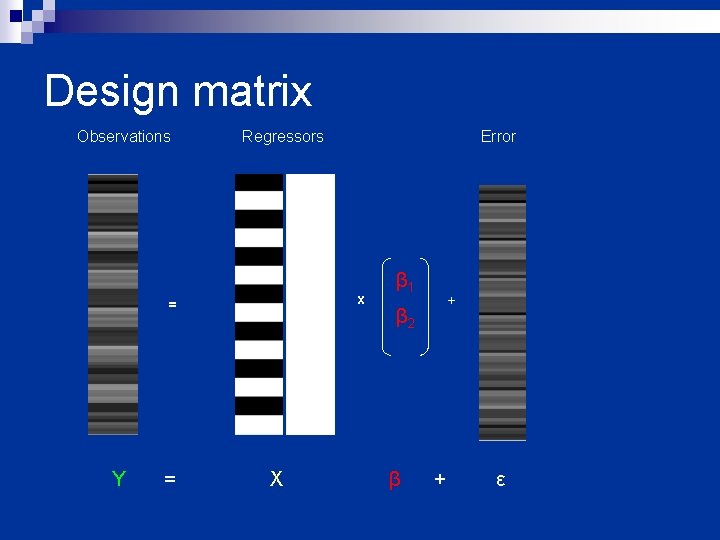
Design matrix Observations Regressors x = Y = Error X β 1 + β 2 β + ε

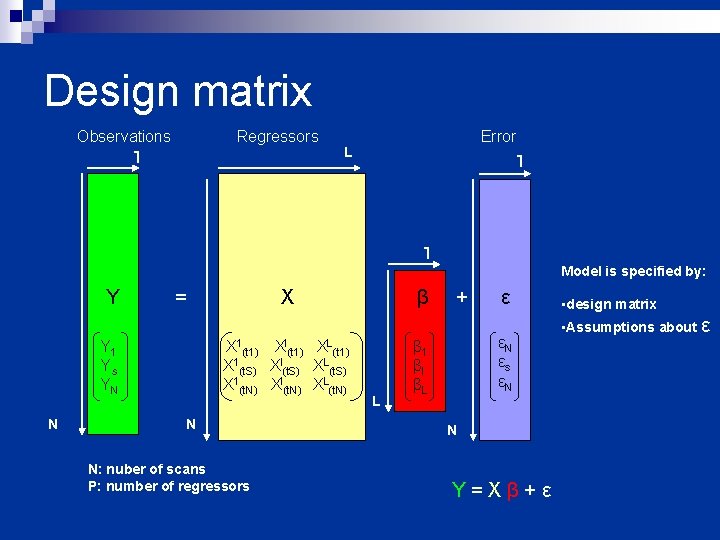
Design matrix Observations Regressors Error L l l l Y = Y 1 Ys YN N β 2 X X 1 (t 1) Xl (t 1) β 1 XL (t 1) X 1(t. S) Xl(t. S) XL(t. S) X 1(t. N) Xl(t. N) XL(t. N) N N: nuber of scans P: number of regressors L Model is specified by: β + ε εN εs εN β 1 βl βL N Y=Xβ+ε • design matrix • Assumptions about ε

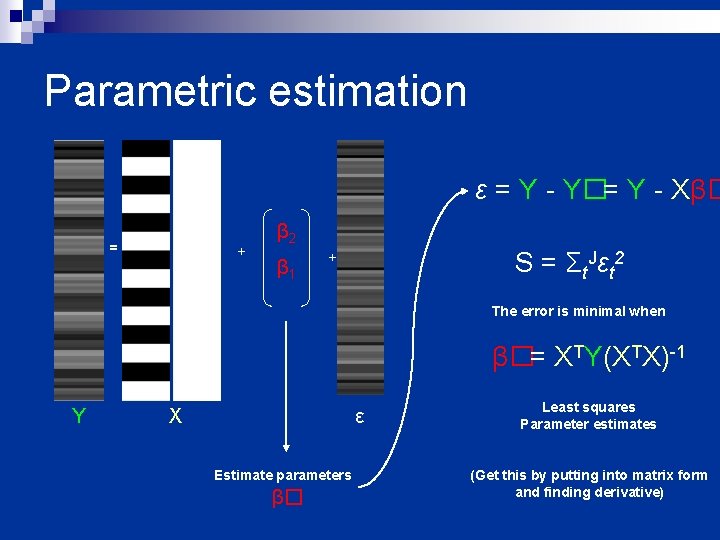
Parametric estimation ε = Y - Y�= Y - Xβ� = + β 2 β 1 S = Σt. Jεt 2 + The error is minimal when β�= XTY(XTX)-1 Y X ε Estimate parameters β� Least squares Parameter estimates (Get this by putting into matrix form and finding derivative)

Summary n The General Linear Model allows you to find the parameters, β, which provide the best fit with your data, Y n The optimal parameters estimates, β, are found by minimising the Sums of Squares differences between your predicted model and the observed data n The design matrix in SPM contains the information about the factors, X, which may explain the observed data n Once we have obtained the βs at each voxel we can use these to do various statistical tests but that is another talk….

THE END Thank you to Lucy, Daniel and Will and to Stephan for his chapter and slides about GLM and to Adam for last year’s presentation Links: http: //www. fil. ion. ucl. ac. uk/~wpenny/notes 03/slides/glm/slide 1. htm http: //www. fil. ion. ucl. ac. uk/spm/HBF 2/pdfs/Ch 7. pdf http: //www. fil. ion. ucl. ac. uk/~wpenny/mfd/GLM. ppt