General Functions A nonperiodic function can be represented

General Functions • A non-periodic function can be represented as a sum of sin’s and cos’s of (possibly) all frequencies: • F( ) is the spectrum of the function f(x)

Fourier Transform • F( ) is computed from f(x) by the Fourier Transform:

Example: Box Function

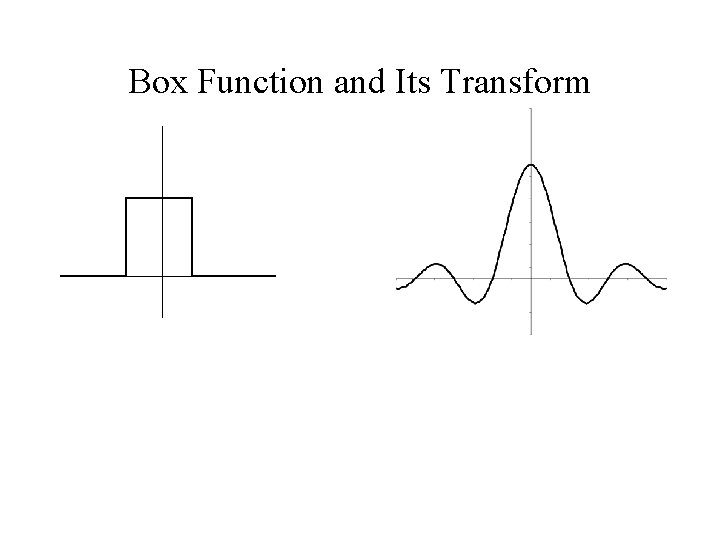
Box Function and Its Transform

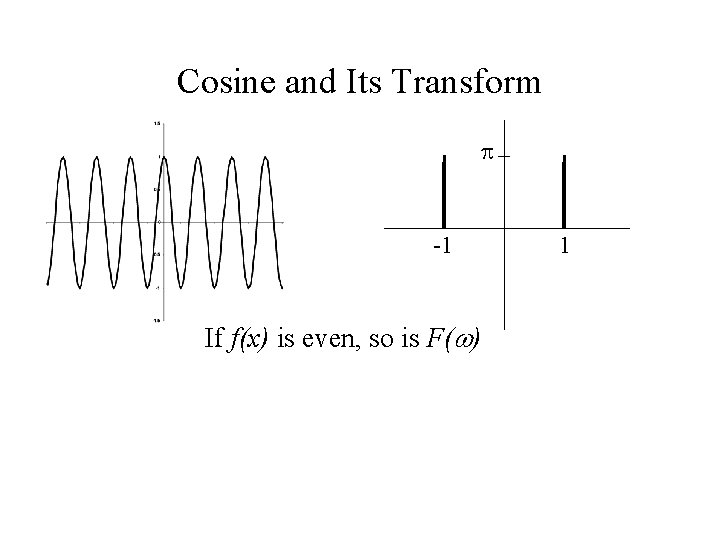
Cosine and Its Transform -1 If f(x) is even, so is F( ) 1

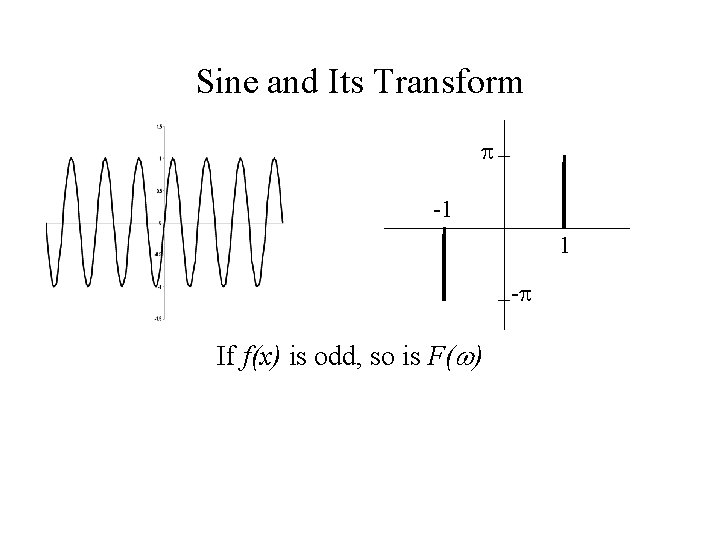
Sine and Its Transform -1 1 - If f(x) is odd, so is F( )

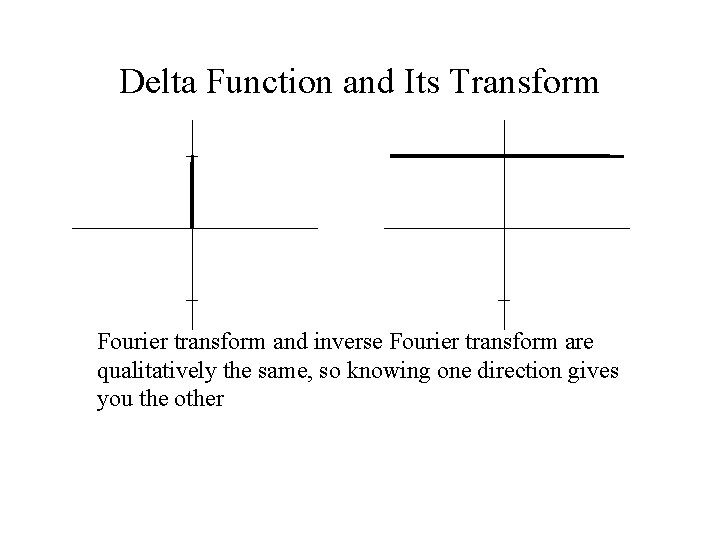
Delta Function and Its Transform Fourier transform and inverse Fourier transform are qualitatively the same, so knowing one direction gives you the other

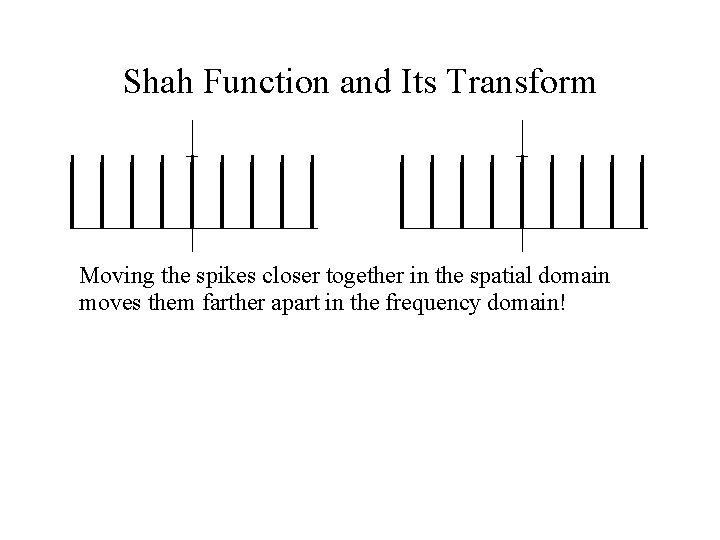
Shah Function and Its Transform Moving the spikes closer together in the spatial domain moves them farther apart in the frequency domain!

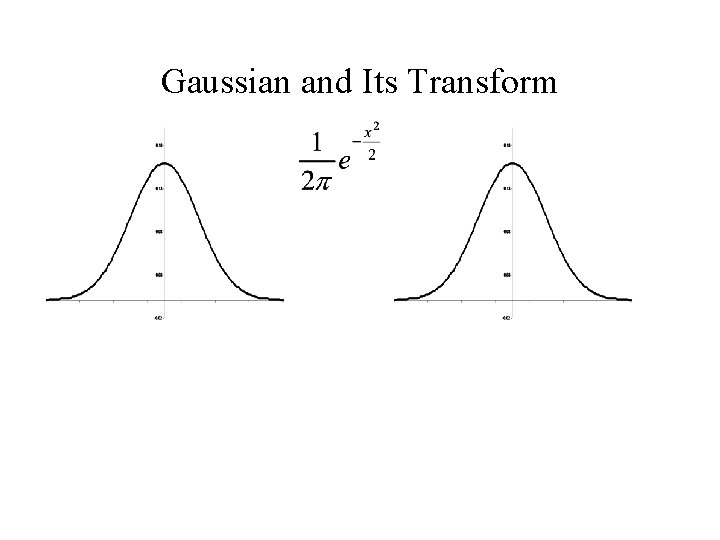
Gaussian and Its Transform

Qualitative Properties • The spectrum of a functions tells us the relative amounts of high and low frequencies – Sharp edges give high frequencies – Smooth variations give low frequencies • A function is bandlimited if its spectrum has no frequencies above a maximum limit – sin, cos are bandlimited – Box, Gaussian, etc are not

Functions to Images • Images are 2 D, discrete functions • 2 D Fourier transform uses product of sin’s and cos’s (things carry over naturally) • Fourier transform of a discrete, quantized function will only contain discrete frequencies in quantized amounts • Numerical algorithm: Fast Fourier Transform (FFT) computes discrete Fourier transforms

2 D Discrete Fourier Transform

Filters • A filter is something that attenuates or enhances particular frequencies • Easiest to visualize in the frequency domain, where filtering is defined as multiplication: • Here, F is the spectrum of the function, G is the spectrum of the filter, and H is the filtered function. Multiplication is point-wise

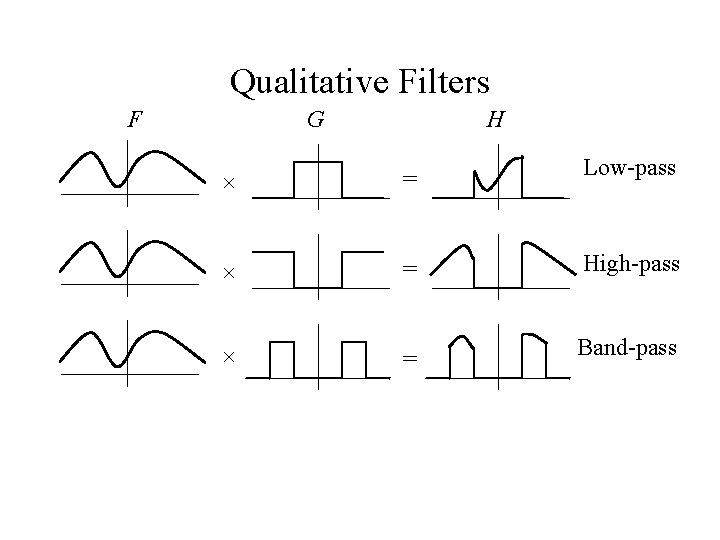
Qualitative Filters F G H = Low-pass = High-pass = Band-pass

Low-Pass Filtered Image

High-Pass Filtered Image

Filtering in the Spatial Domain • Filtering the spatial domain is achieved by convolution • Qualitatively: Slide the filter to each position, x, then sum up the function multiplied by the filter at that position

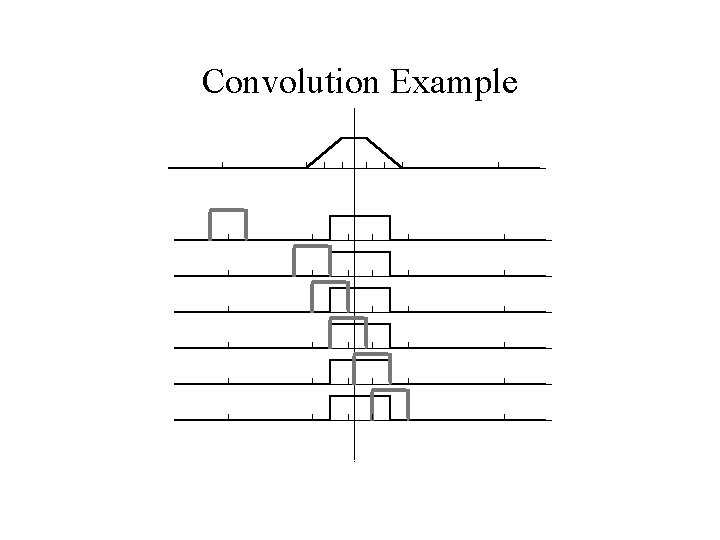
Convolution Example

Convolution Theorem • Convolution in the spatial domain is the same as multiplication in the frequency domain – – – Take a function, f, and compute its Fourier transform, F Take a filter, g, and compute its Fourier transform, G Compute H=F G Take the inverse Fourier transform of H, to get h Then h=f g • Multiplication in the spatial domain is the same as convolution in the frequency domain

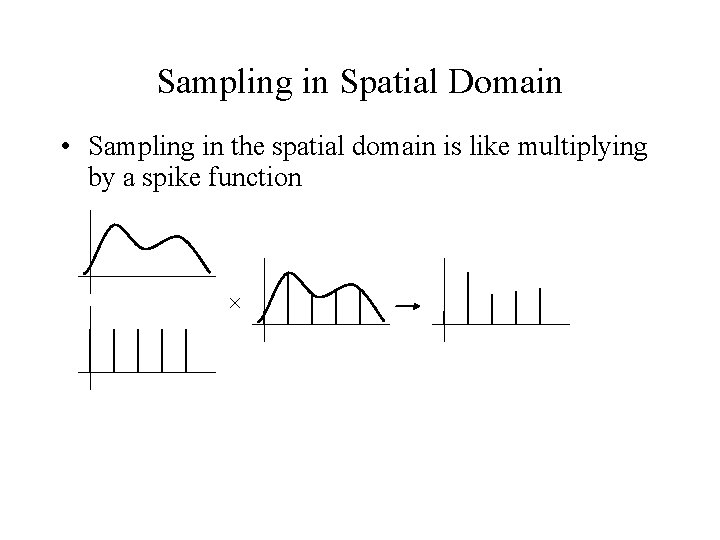
Sampling in Spatial Domain • Sampling in the spatial domain is like multiplying by a spike function

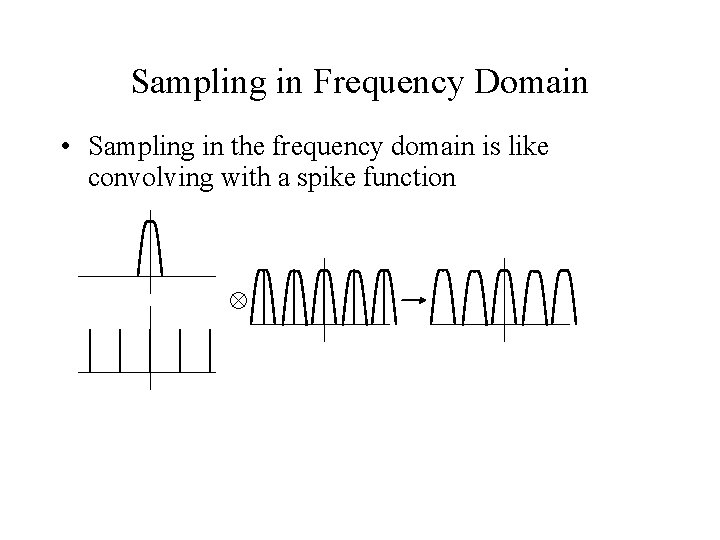
Sampling in Frequency Domain • Sampling in the frequency domain is like convolving with a spike function

Reconstruction in Frequency Domain • To reconstruct, we must restore the original spectrum • That can be done by multiplying by a square pulse

Reconstruction in Spatial Domain • Multiplying by a square pulse in the frequency domain is the same as convolving with a sinc function in the spatial domain

Aliasing Due to Under-sampling • If the sampling rate is too low, high frequencies get reconstructed as lower frequencies • High frequencies from one copy get added to low frequencies from another

Aliasing Implications • There is a minimum frequency with which functions must be sampled – the Nyquist frequency – Twice the maximum frequency present in the signal • Signals that are not bandlimited cannot be accurately sampled and reconstructed • Not all sampling schemes allow reconstruction – eg: Sampling with a box

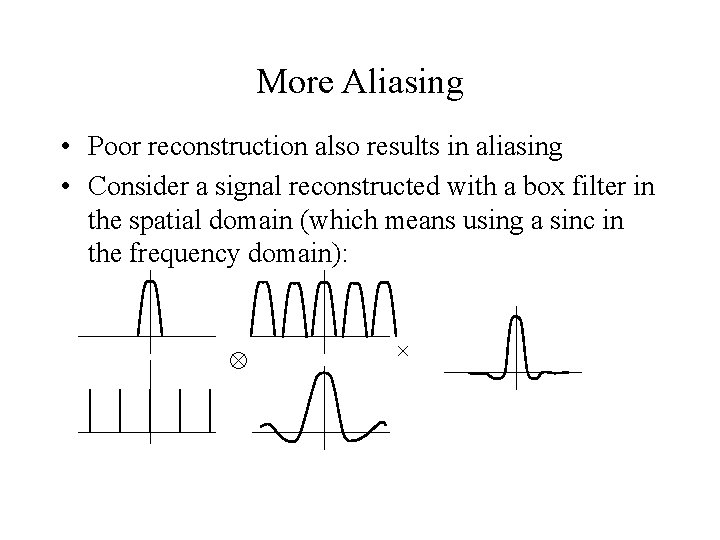
More Aliasing • Poor reconstruction also results in aliasing • Consider a signal reconstructed with a box filter in the spatial domain (which means using a sinc in the frequency domain):