General Features of Enzymes Most biological reactions are

General Features of Enzymes • • Most biological reactions are catalyzed by enzymes Most enzymes are proteins Highly specific (in reaction & reactants) Involvement of cofactor or coenzyme in some enzymes (prosthetic groups, holoenzyme, apoenzyme) • Activity regulated through – Feedback inhibition – Regulatory proteins (e. g. calmodulin) – Covalent modification (e. g. phosphorylation) – Precursor to mature form transition (proteolytic activation)
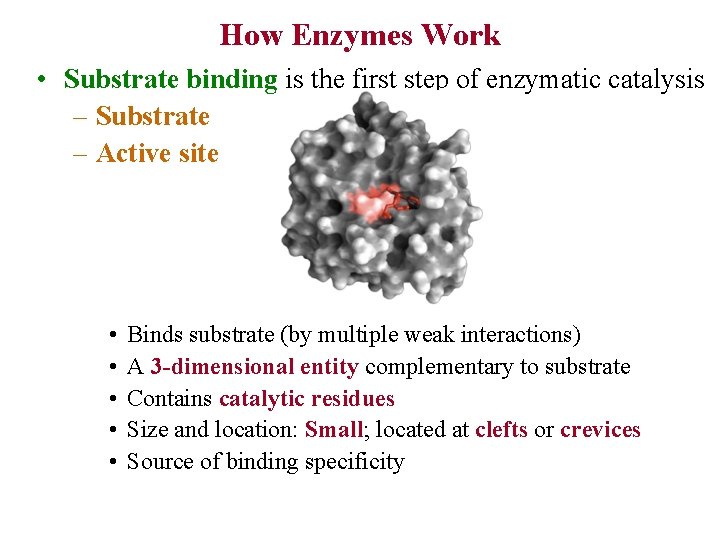
How Enzymes Work • Substrate binding is the first step of enzymatic catalysis – Substrate – Active site • • • Binds substrate (by multiple weak interactions) A 3 -dimensional entity complementary to substrate Contains catalytic residues Size and location: Small; located at clefts or crevices Source of binding specificity
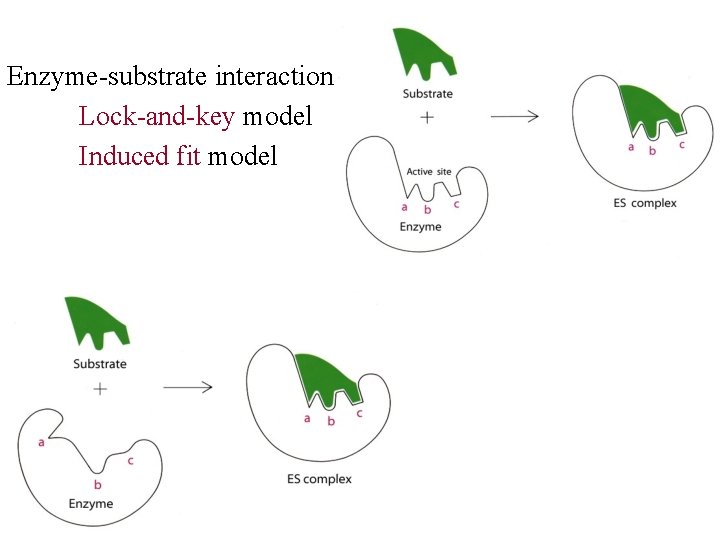
Enzyme-substrate interaction: Lock-and-key model Induced fit model
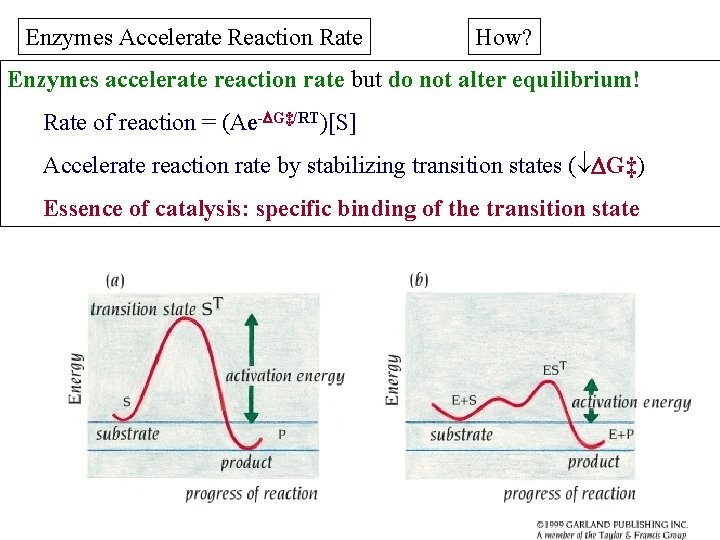
Enzymes Accelerate Reaction Rate How? Enzymes accelerate reaction rate but do not alter equilibrium! Rate of reaction = (Ae- G‡/RT)[S] Accelerate reaction rate by stabilizing transition states ( G‡) Essence of catalysis: specific binding of the transition state

Michaelis-Menten Model Accounts for Kinetic Properties of many Enzyme • Kinetic properties of many enzymes (V vs. [S] plot) • Michaelis-Menten Model k 1 k 3 E+S ES E+P k 2 – Purpose: using the model to derive an expression relating rate of reaction to [E] and [S] and k 1, k 2, and k 3 – Assumption #1: no product reverts to initial substrate (initial state) – Assumption #2: steady state ([ES] is constant) • k 1[E][S]=k 2[ES]+k 3[ES], so [ES] = [E][S]/KM ; KM =(k 2+k 3)/k 1 • [E] = [ET] - [ES]; [S] = [ST] - [ES] - [P] • work under the following condition: [ET] << [ST] ; and at initial time, so [P] is negligible, and so [S] = [ST] [ES] = [ET] [S]/(KM + [S]) so, V = k 3 [ES] = k 3[ET] [S]/(KM + [S]) = Vmax [S]/(KM + [S])
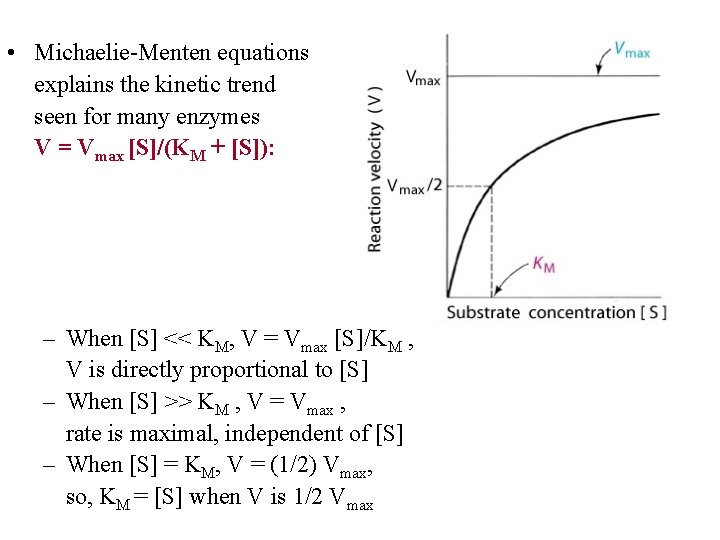
• Michaelie-Menten equations explains the kinetic trend seen for many enzymes V = Vmax [S]/(KM + [S]): – When [S] << KM, V = Vmax [S]/KM , V is directly proportional to [S] – When [S] >> KM , V = Vmax , rate is maximal, independent of [S] – When [S] = KM, V = (1/2) Vmax, so, KM = [S] when V is 1/2 Vmax
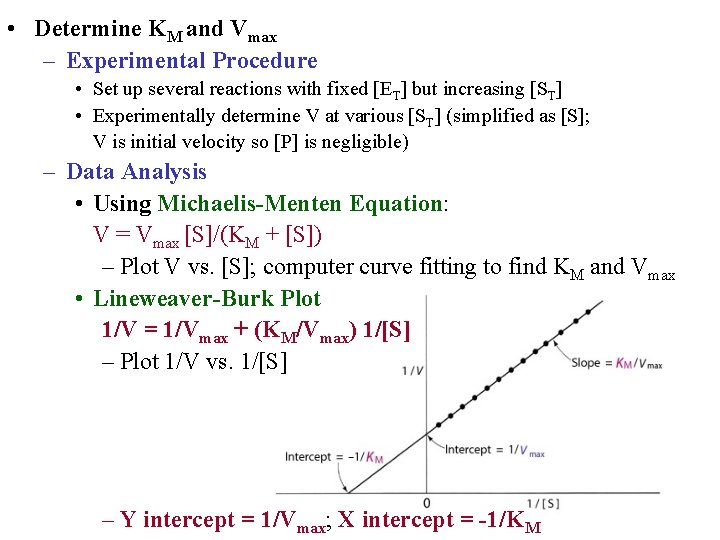
• Determine KM and Vmax – Experimental Procedure • Set up several reactions with fixed [ET] but increasing [ST] • Experimentally determine V at various [ST] (simplified as [S]; V is initial velocity so [P] is negligible) – Data Analysis • Using Michaelis-Menten Equation: V = Vmax [S]/(KM + [S]) – Plot V vs. [S]; computer curve fitting to find KM and Vmax • Lineweaver-Burk Plot 1/V = 1/Vmax + (KM/Vmax) 1/[S] – Plot 1/V vs. 1/[S] – Y intercept = 1/Vmax; X intercept = -1/KM

Kinetic Perfection in Enzymatic Catalysis • For Enzymes that Obey Michaelis-Menten Model – When all enzyme molecules are saturated with substrate • V = Vmax = k 3 [ET], rate constant is k 3 (= kcat) – When [S] << KM and so most of the active sites are unoccupied • V = k 3 [ES]= k 3 [E][S]/KM as [S] << KM, so [E] [ET], so V = k 3 [ET][S]/KM = (k 3/KM)[ET][S] so V depends on k 3 / KM: k 3 / KM= k 3 k 1 / (k 2 + k 3) < k 1 cannot be faster than diffusion controlled encounter of an enzyme and its substrate, which is 108 to 109 M-1 s-1 So, the upper limit of k 3 / KM is 108 to 109 M-1 s-1. • For Enzymes that Do not Obey Michaelis-Menten Model – When all E are saturated with S, rate depends on k cat; kcat k 3 – When not all E are saturated with S, rate depends on k cat / KM • Some enzymes having k 3/KM of 108 - 109 M-1 s-1 reached kinetic perfection! Their catalytic velocity is limited by the rate at which they encounter substrate in the solution.

Enzyme Inhibition • Irreversible Inhibition – Inhibitor destroys a functional group on the enzyme – Or inhibitor binds to the enzyme very tightly (covalently or noncovalently) dissociates very slowly from enzyme • Reversible Inhibition

• Reversible Inhibition – Inhibitor binds and dissociate rapidly from the enzyme – Competitive inhibitor • Inhibitor binds at active site; compete for binding with substrate; exist as either ES or EI; no ESI • Inhibitor structure resembles that of substrate • Overcome competitive inhibition by increasing [S] – Noncompetitive inhibitor • Inhibitor binds at a site other than active site • Binding of noncompetitive inhibitor decreases turnover number (reduces k 3)

Kinetics of Enzyme Inhibition • Assume the enzyme exhibits Michaelis-Menten Kinetics – Set up enzymatic reactions with fixed [ET] but increasing [ST] – One set without inhibitor and another set with inhibitor – Plot 1/V vs. 1/[S] (Lineweaver-Burk Plot)

Kinetics of Enzyme Inhibition • Competitive Inhibition – The two lines on the plot have the same Y intercept (Same V max) – KM and KIM are different : KIM = KM (1 + [I]/KI) KI = [E][I]/[EI] (for E + I EI) – 1/V = 1/Vmax + KM/Vmax (1 + [I]/KI) (1/[S]) – KM and KIM can be determined from the Lineweaver-Burk plot – KM’ = KM (1 + [I]/KI) allows the determination of KI – Inhibition can be overcome by increasing [S]

Kinetics of Enzyme Inhibition • Noncompetitive Inhibition – – Same KM in the presence and absence of Inhibitor Smaller V max in the presence of Inhibitor VI max = V max /(1 + [I]/KI) VI max and V max can be determined from the Lineweaver. Burk plot – VI max = V max /(1 + [I]/KI) allows the determination of KI – Cannot be overcome by increasing [S]
- Slides: 13