General Addition Rule AP Statistics Addition Rule for

General Addition Rule AP Statistics

Addition Rule for Disjoint Events If two events A and B are disjoint: P(A or B) = P(A) + P(B) If three events are disjoint: P(A or B or C) = P(A) + P(B) + P(C)

Mutually Exclusive (Disjoint) Events • Two events have no outcomes in common. • Example: An animal can’t be a dog and a cat at the same time. • Example: Roll a “ 2” or a “ 5” – these can’t happen at the same time. • Note: the second “or” statement involves only one roll of the die, not two rolls.

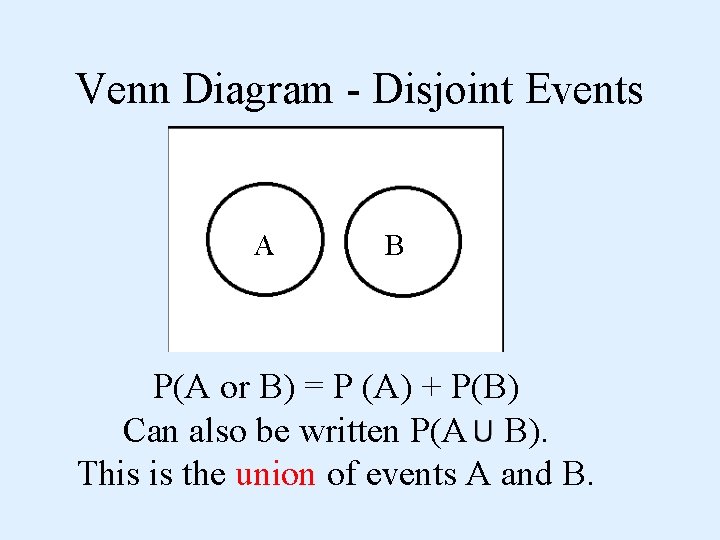
Venn Diagram - Disjoint Events A B P(A or B) = P (A) + P(B) Can also be written P(A B). This is the union of events A and B.

Non –Disjoint Events: Can Have Outcomes in Common. If two events E & F are not disjoint, • P(E or F) = P(E) + P(F) – P(E and F) • This is The General Addition Rule. • P(E and F) is called a joint probability and can be written P(E∩F). • P(E∩F) is also called the intersection of events E and F.

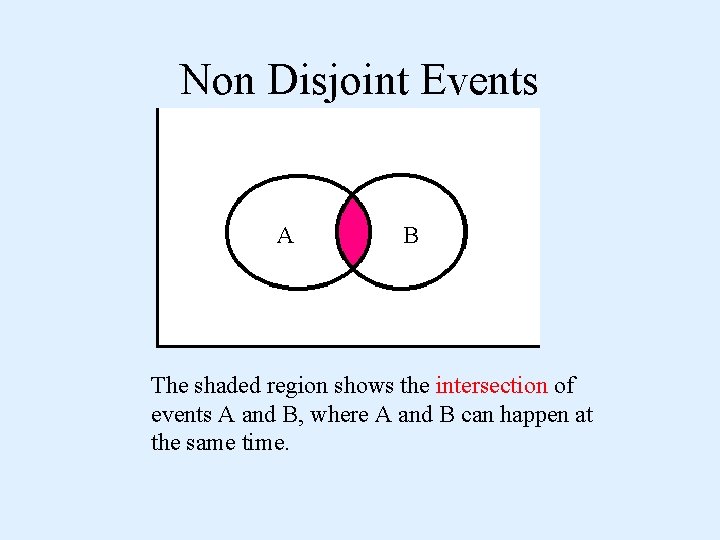
Non Disjoint Events A B The shaded region shows the intersection of events A and B, where A and B can happen at the same time.

Example • Event A = (Being a senior at CRHS) • Event B = (Taking Statistics) • You can have seniors at CRHS who are taking Stats! These events can happen at the same time.

Example 6. 17 on page 362 • • • P (Deb becoming a partner) =. 7 P (Matt becoming a partner) =. 5 P (Deb and Matt becoming a partner) =. 3 P(Deb or Matt becoming a partner) = 1. 2? ? This probability exceeds 1 which is impossible!

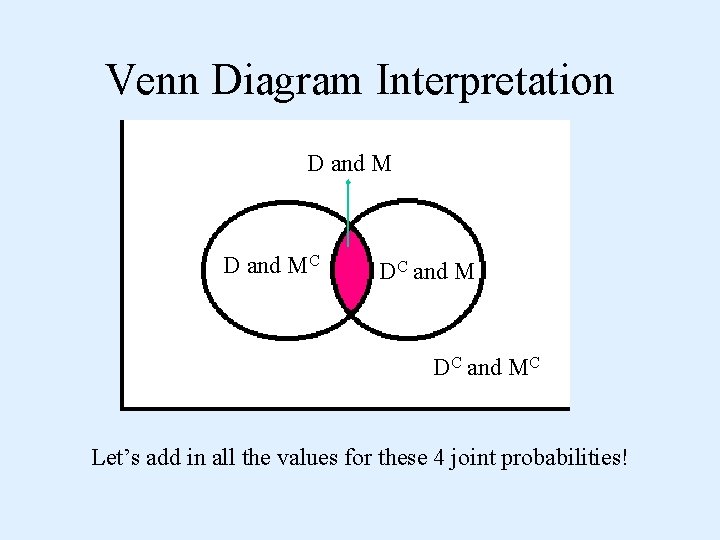
Venn Diagram Interpretation D and MC DC and MC Let’s add in all the values for these 4 joint probabilities!

Example 6. 17 Continued • P(at least one is promoted) = P(Deb or Matt) • =. 7 +. 5 -. 3 =. 9 • P(neither is promoted) = 1 -. 9 =. 1 • The reason that we “correct” by subtracting. 3 (the intersection of Deb and Matt) is that if we don’t, it is counted twice.

Union • The union of event A with event B consists of all outcomes that are in at least one of the two events. • Example: Event E is rolling a die and getting prime number or even number. • E = {2, 3, 4, 5, 6}

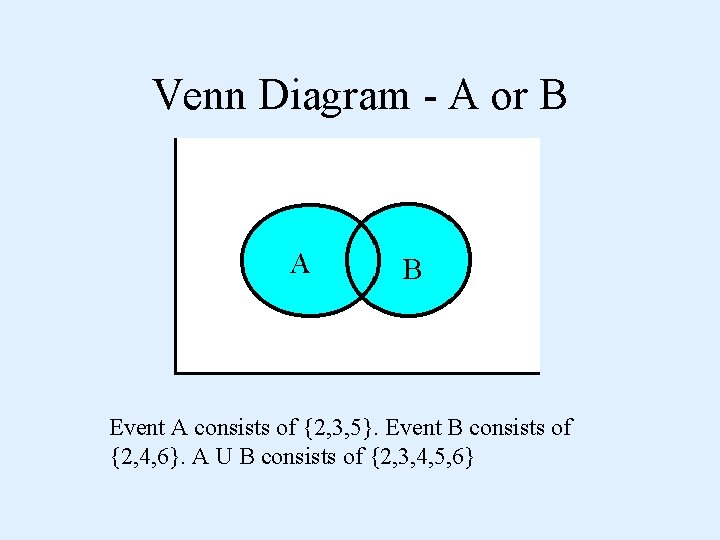
Venn Diagram - A or B A B Event A consists of {2, 3, 5}. Event B consists of {2, 4, 6}. A U B consists of {2, 3, 4, 5, 6}

Intersection • This is the event where both A and B happen. • It consists of all outcomes that are in both events. • Denoted:

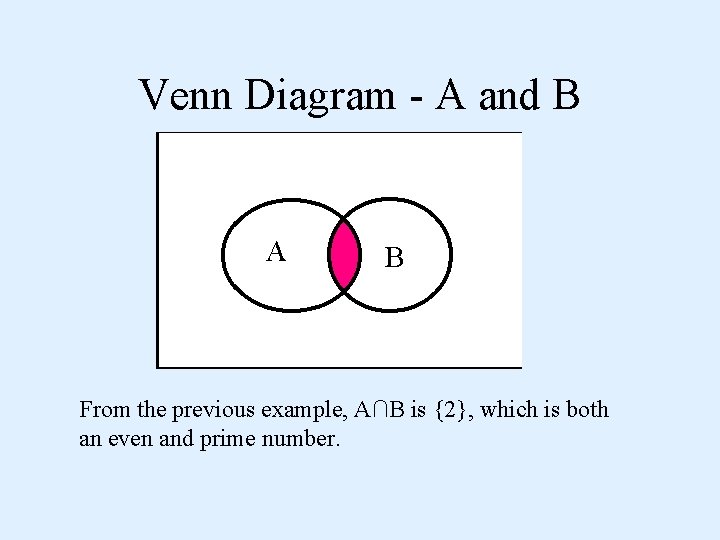
Venn Diagram - A and B A B From the previous example, A∩B is {2}, which is both an even and prime number.

General Rule for the Union of Two Events • P(A or B) = P(A) + P(B) – P(A and B). • Note: if there is no intersection (if A and B are mutually exclusive), then the term: P(A and B) is equal to zero, which returns us to the Addition Rule for Disjoint Events.

Homework • Worksheet