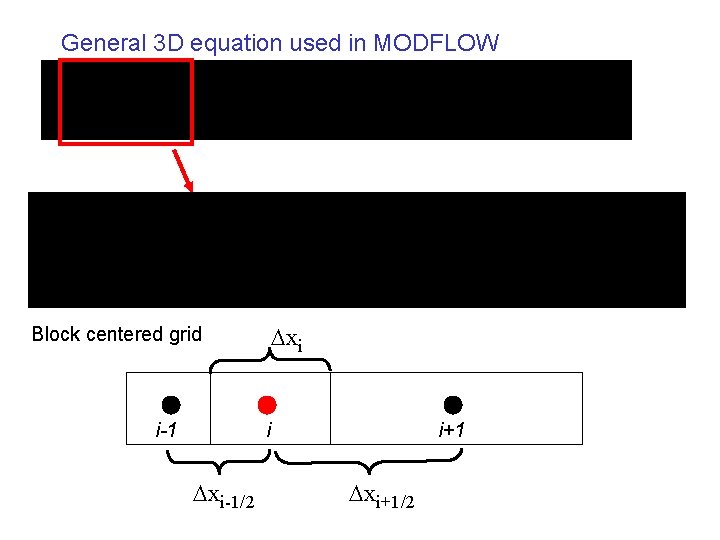
General 3 D equation used in MODFLOW xi

General 3 D equation used in MODFLOW xi Block centered grid i-1 i xi-1/2 i+1 xi+1/2

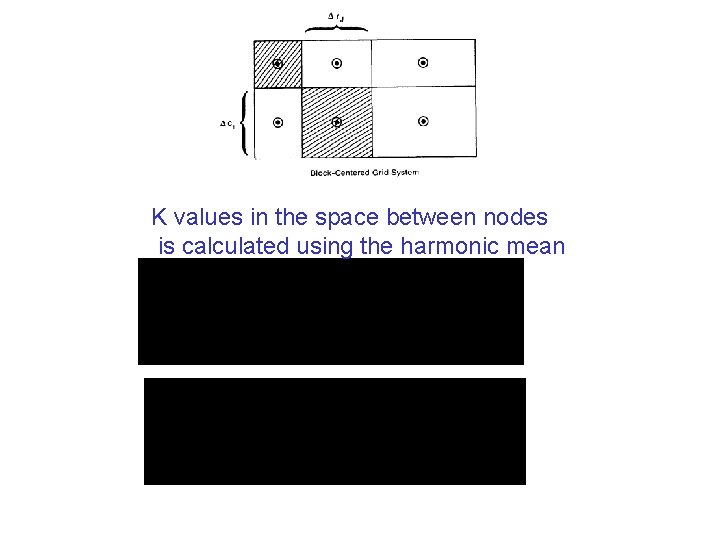
K values in the space between nodes is calculated using the harmonic mean

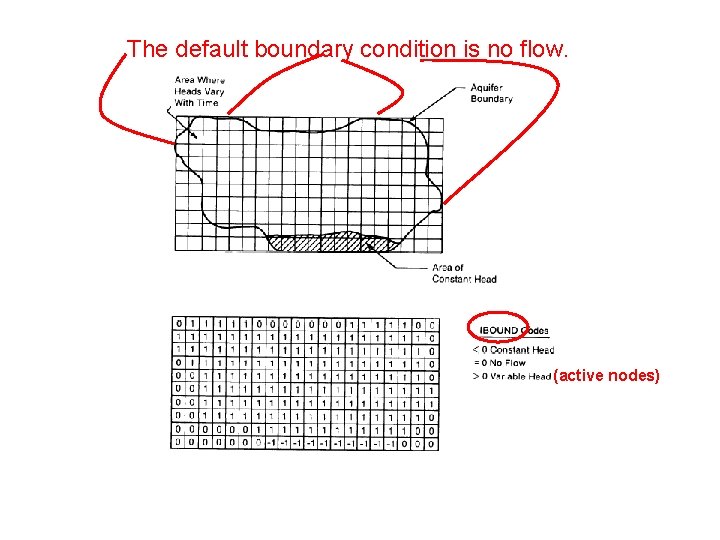
The default boundary condition is no flow. (active nodes)

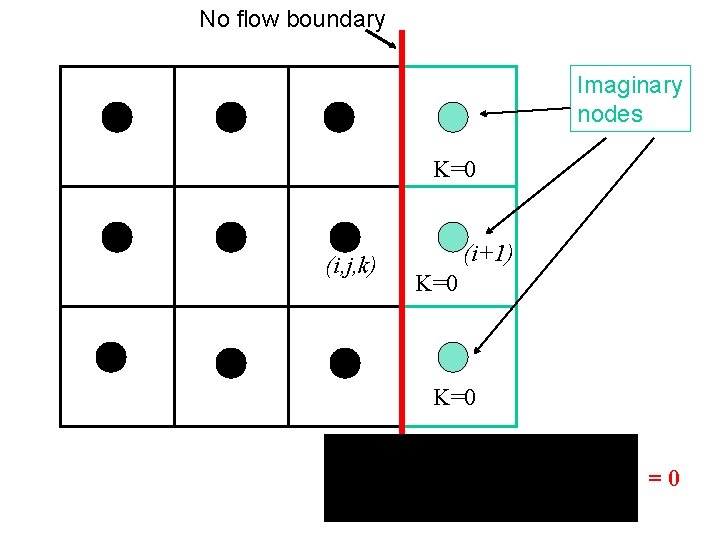
No flow boundary Imaginary nodes K=0 (i, j, k) (i+1) K=0 =0

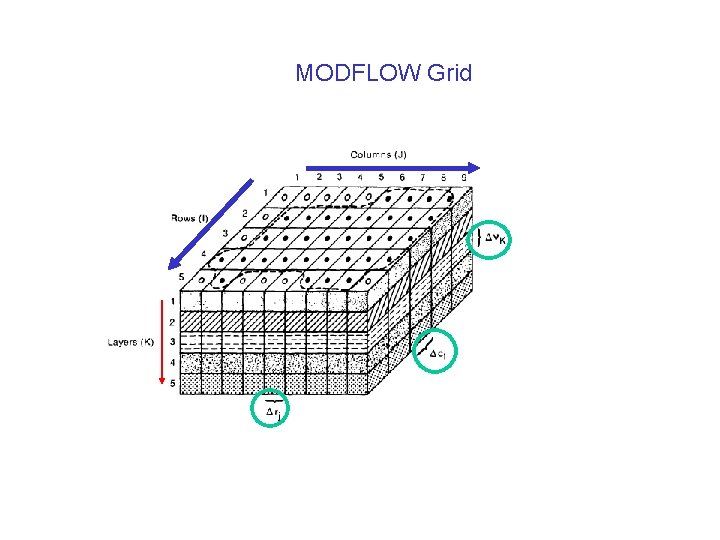
MODFLOW Grid

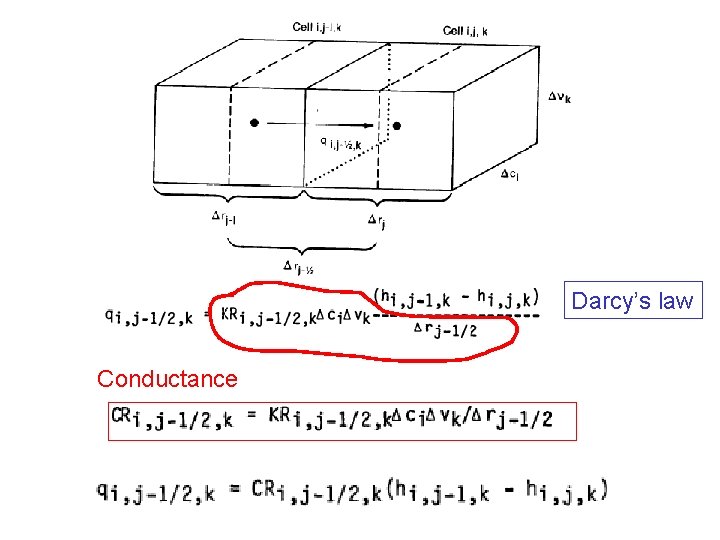
Darcy’s law Conductance

In general, conductance = KA/ L Also: leakance = Kv/thickness resistance = thickness/Kv (resistance is an analytic element term)

Vertical Conductance Terms MODFLOW uses special terms (VCONT) for vertical conductance, which is required in 3 D problems. Modflow. exe requires the user to supply values for the VCONT arrays. GW Vistas computes the values in the VCONT arrays for you. VCONT = Kv/ z = Conductance/( x y) = “leakance”

Vertical conductance is defined using leakance, or VCONT in MODFLOW language. We also have horizontal conductance along rows and along columns.

See MODFLOW manual (p. 2 -19) or 2 nd ed. of textbook by Domenico & Schwartz (Eqn. 7. 15) for MODFLOW’s FD equation

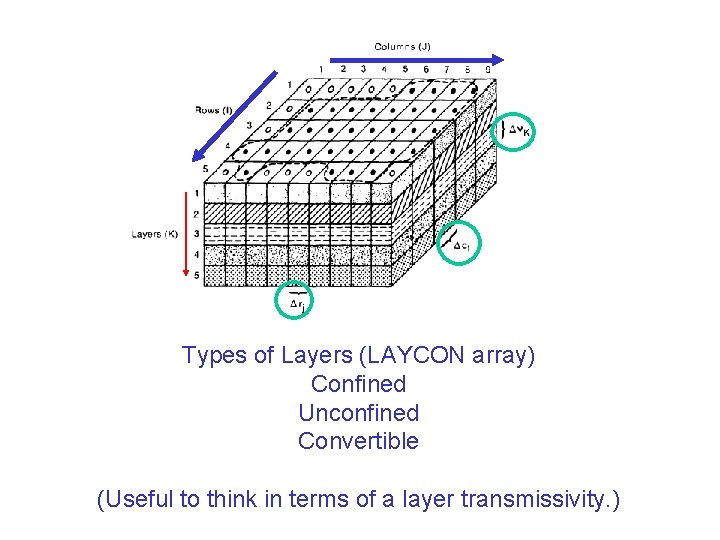
Types of Layers (LAYCON array) Confined Unconfined Convertible (Useful to think in terms of a layer transmissivity. )

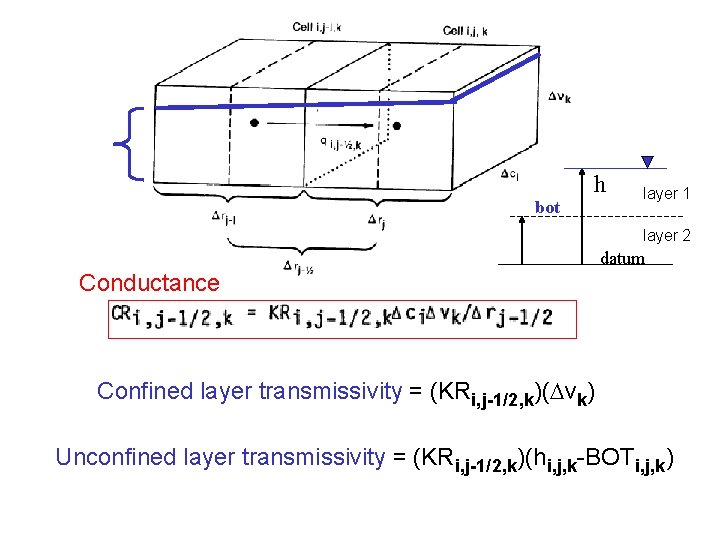
bot h layer 1 layer 2 datum Conductance Confined layer transmissivity = (KRi, j-1/2, k)( vk) Unconfined layer transmissivity = (KRi, j-1/2, k)(hi, j, k-BOTi, j, k)

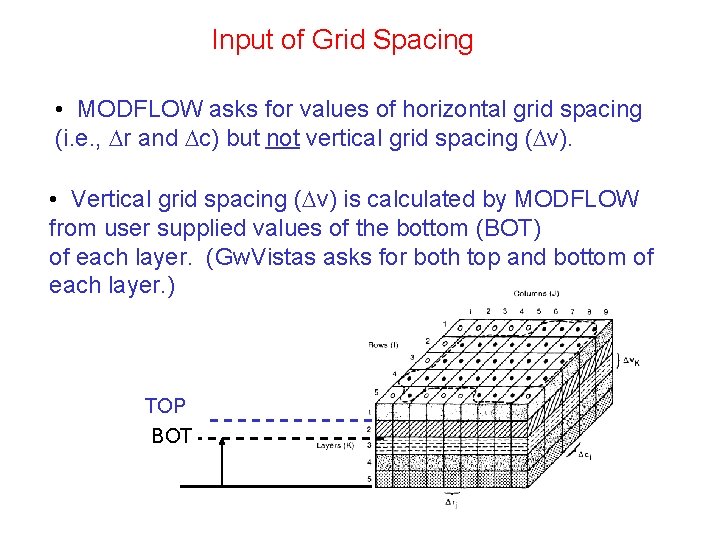
Input of Grid Spacing • MODFLOW asks for values of horizontal grid spacing (i. e. , r and c) but not vertical grid spacing ( v). • Vertical grid spacing ( v) is calculated by MODFLOW from user supplied values of the bottom (BOT) of each layer. (Gw. Vistas asks for both top and bottom of each layer. ) TOP BOT

Note that a top unconfined layer actually has no top. The head value in the top layer could potentially rise to infinity. Land surface elevation is not used in MODFLOW, except in the ET package.

Examples of solution techniques that combine matrix solution with iteration: IADI (see chapter 5 of W&A) SSOR* SIP* PCG 2* *Used in MODFLOW

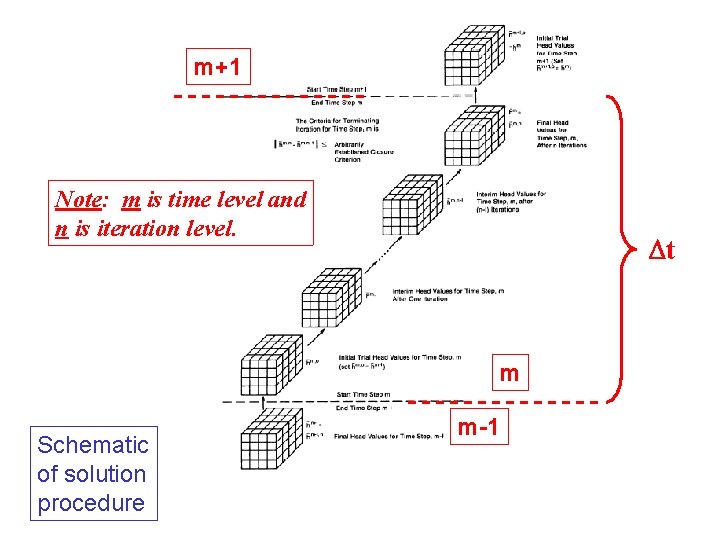
m+1 Note: m is time level and n is iteration level. t m Schematic of solution procedure m-1

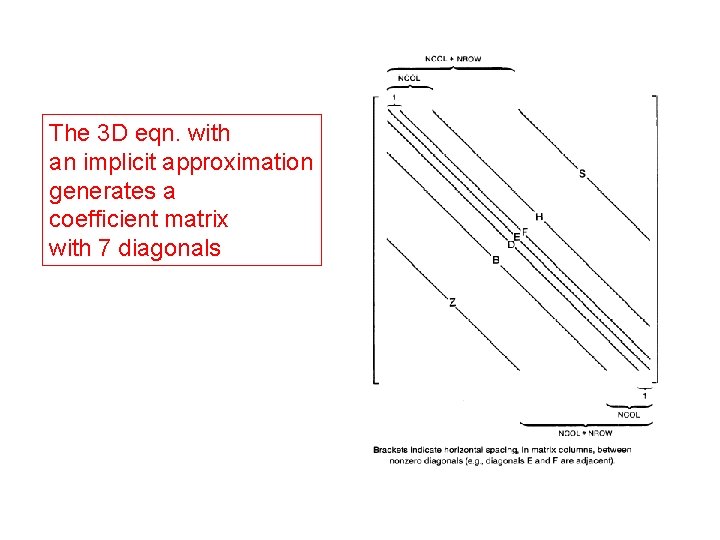
The 3 D eqn. with an implicit approximation generates a coefficient matrix with 7 diagonals

Coefficient Matrix for a model with 2 rows, 3 columns, 2 layers. Matrix is sparse and symmetric.

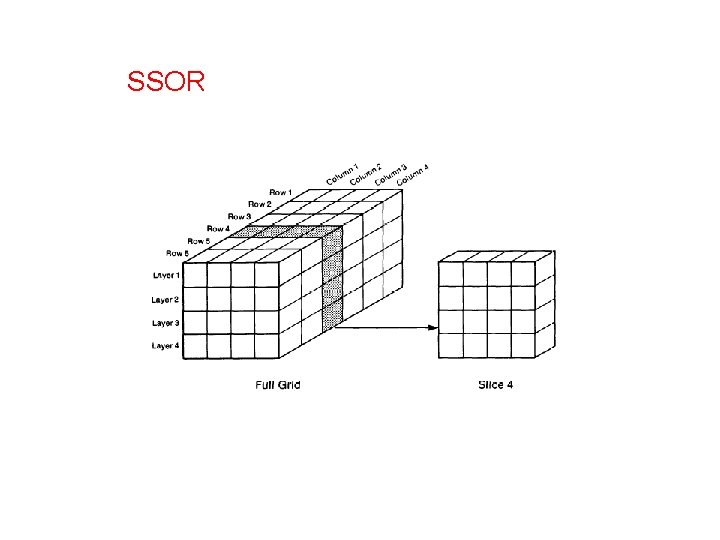
SSOR

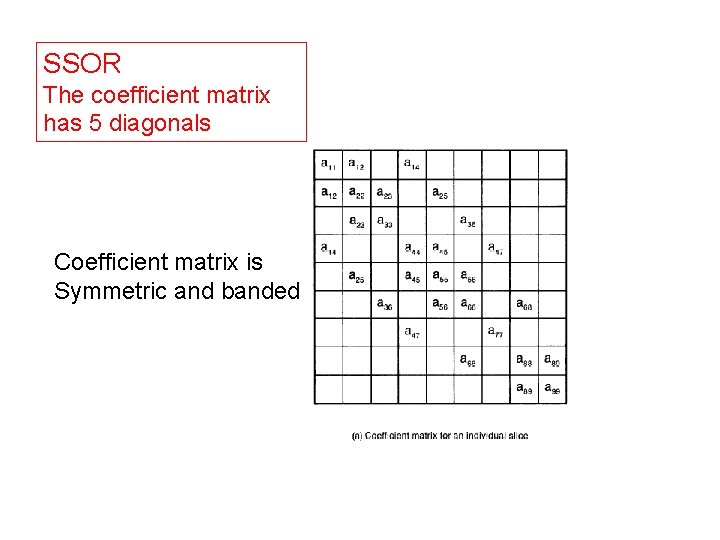
SSOR The coefficient matrix has 5 diagonals Coefficient matrix is Symmetric and banded

From MODFLOW manual

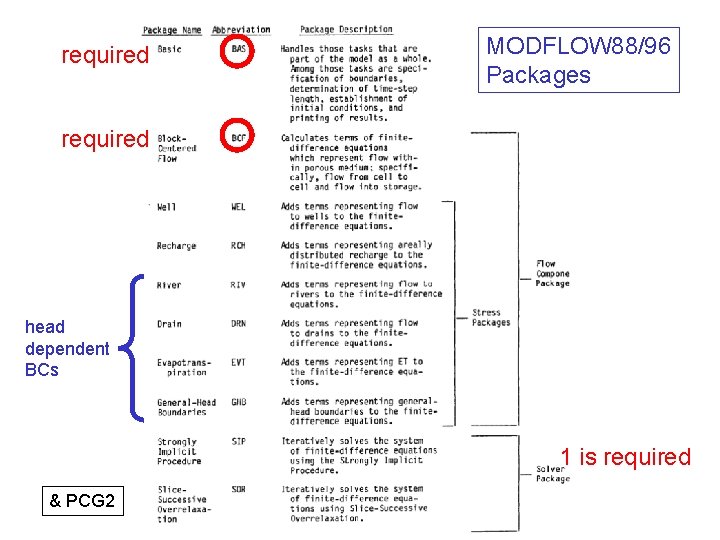
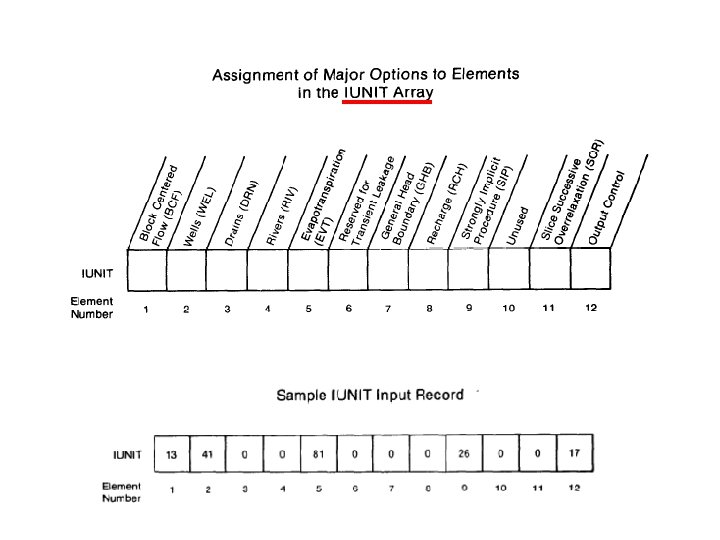
required MODFLOW 88/96 Packages required head dependent BCs 1 is required & PCG 2

Input assembly for the BAS Package