General 2 k Factorial Designs Used to explain

  • Slides: 26
Download presentation
General 2 k Factorial Designs • Used to explain the effects of k factors,

General 2 k Factorial Designs • Used to explain the effects of k factors, each with two alternatives or levels • 22 factorial designs are a special case • Methods developed there extend to the more general case • But many more possible interactions between pairs (and trios, etc. ) of factors © 1998, Geoff Kuenning

2 k Factorial Designs With Replications • 2 k factorial designs do not allow

2 k Factorial Designs With Replications • 2 k factorial designs do not allow for estimation of experimental error – No experiment is ever repeated • But usually experimental error is present – And often it’s important • Handle the issue by replicating experiments • But which to replicate, and how often? © 1998, Geoff Kuenning

2 kr Factorial Designs • Replicate each experiment r times • Allows quantification of

2 kr Factorial Designs • Replicate each experiment r times • Allows quantification of experimental error • Again, easiest to first look at the case of only 2 factors © 1998, Geoff Kuenning

22 r Factorial Designs • 2 factors, 2 levels each, with r replications at

22 r Factorial Designs • 2 factors, 2 levels each, with r replications at each of the four combinations • y = q 0 + q. Ax. A + q. Bx. B + q. ABx. Ax. B + e • Now we need to compute effects, estimate the errors, and allocate variation • We can also produce confidence intervals for effects and predicted responses © 1998, Geoff Kuenning

Computing Effects for 22 r Factorial Experiments • We can use the sign table,

Computing Effects for 22 r Factorial Experiments • We can use the sign table, as before • But instead of single observations, regress off the mean of the r observations • Compute errors for each replication using similar tabular method • Similar methods used for allocation of variance and calculating confidence intervals © 1998, Geoff Kuenning

Example of 22 r Factorial Design With Replications • Same Time Warp system as

Example of 22 r Factorial Design With Replications • Same Time Warp system as before, but with 4 replications at each point (r=4) • No DLM, 8 nodes - 820, 822, 813, 809 • DLM, 8 nodes - 776, 798, 750, 755 • No DLM, 64 nodes - 217, 228, 215, 221 • DLM, 64 nodes - 197, 180, 220, 185 © 1998, Geoff Kuenning

22 r Factorial Example Analysis Matrix I 1 1 A -1 1 B -1

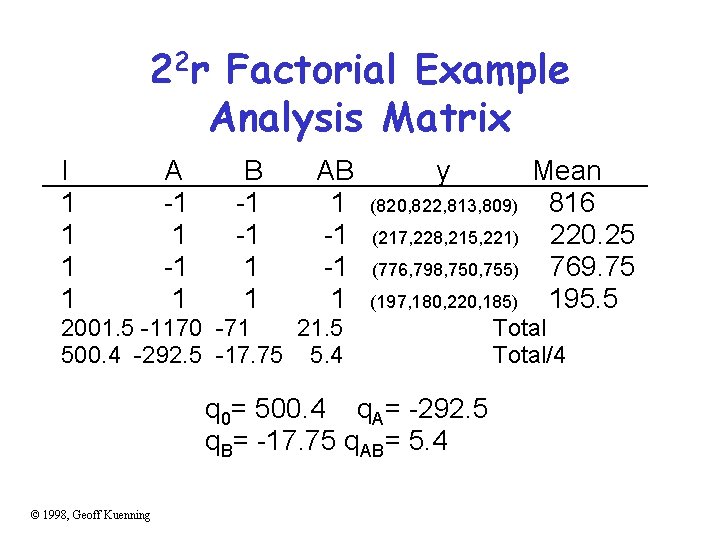
22 r Factorial Example Analysis Matrix I 1 1 A -1 1 B -1 -1 1 1 AB 1 -1 -1 1 y (820, 822, 813, 809) (217, 228, 215, 221) (776, 798, 750, 755) (197, 180, 220, 185) 2001. 5 -1170 -71 21. 5 500. 4 -292. 5 -17. 75 5. 4 q 0= 500. 4 q. A= -292. 5 q. B= -17. 75 q. AB= 5. 4 © 1998, Geoff Kuenning Mean 816 220. 25 769. 75 195. 5 Total/4

Estimation of Errors for 22 r Factorial Example • Figure differences between predicted and

Estimation of Errors for 22 r Factorial Example • Figure differences between predicted and observed values for each replication N yi • Now calculate SSE © 1998, Geoff Kuenning

Allocating Variation • We can determine the percentage of variation due to each factor’s

Allocating Variation • We can determine the percentage of variation due to each factor’s impact – Just like 2 k designs without replication • But we can also isolate the variation due to experimental errors • Methods are similar to other regression techniques for allocating variation © 1998, Geoff Kuenning

Variation Allocation in Example • We’ve already figured SSE • We also need SST,

Variation Allocation in Example • We’ve already figured SSE • We also need SST, SSA, SSB, and SSAB • Also, SST = SSA + SSB + SSAB + SSE • Use same formulae as before for SSA, SSB, and SSAB © 1998, Geoff Kuenning

Sums of Squares for Example • • SST = SSY - SS 0 =

Sums of Squares for Example • • SST = SSY - SS 0 = 1, 377, 009. 75 SSA = 1, 368, 900 SSB = 5041 SSAB = 462. 25 Percentage of variation for A is 99. 4% Percentage of variation for B is 0. 4% Percentage of variation for A/B interaction is 0. 03% • And 0. 2% (apx. ) is due to experimental errors © 1998, Geoff Kuenning

Confidence Intervals For Effects • Computed effects are random variables • Thus, we would

Confidence Intervals For Effects • Computed effects are random variables • Thus, we would like to specify how confident we are that they are correct • Using the usual confidence interval methods • First, must figure Mean Square of Errors © 1998, Geoff Kuenning

Calculating Variances of Effects • Variance of all effects is the same - •

Calculating Variances of Effects • Variance of all effects is the same - • So standard deviation is also the same • In calculations, use t- or z-value for 22 (r-1) degrees of freedom © 1998, Geoff Kuenning

Calculating Confidence Intervals for Example • At 90% level, using the t-value for 12

Calculating Confidence Intervals for Example • At 90% level, using the t-value for 12 degrees of freedom, 1. 782 • And standard deviation of effects is 3. 68 • Confidence intervals are qi-+(1. 782)(3. 68) • q 0 - (493. 8, 506. 9) • q. A - (-299. 1, -285. 9) • q. B - (-24. 3, -11. 2) • q. AB - (-1. 2, 11. 9) © 1998, Geoff Kuenning

Predicted Responses • We already have predicted all the means we can predict from

Predicted Responses • We already have predicted all the means we can predict from this kind of model – We measured four, we can “predict” four • However, we can predict how close we would get to the sample mean if we ran m more experiments © 1998, Geoff Kuenning

Formula for Predicted Means • For m future experiments, the predicted mean is N

Formula for Predicted Means • For m future experiments, the predicted mean is N y ! Where N ym © 1998, Geoff Kuenning N ym

Example of Predicted Means • What would we predict as a confidence interval of

Example of Predicted Means • What would we predict as a confidence interval of the response for no dynamic load management at 8 nodes for 7 more tests? N y 7 • 90% confidence interval is (811. 6, 820. 4) – We’re 90% confident that the mean would be in this range © 1998, Geoff Kuenning

Visual Tests for Verifying Assumptions • What assumptions have we been making? – –

Visual Tests for Verifying Assumptions • What assumptions have we been making? – – – Model errors are statistically independent Model errors are additive Errors are normally distributed Errors have constant standard deviation Effects of errors are additive • Which boils down to independent, normally distributed observations with constant variance © 1998, Geoff Kuenning

Testing for Independent Errors • Compute residuals and make a scatter plot • Trends

Testing for Independent Errors • Compute residuals and make a scatter plot • Trends indicate a dependence of errors on factor levels – But if residuals order of magnitude below predicted response, trends can be ignored • Sometimes a good idea to plot residuals vs. experiments number © 1998, Geoff Kuenning

Example Plot of Residuals vs. Predicted Response © 1998, Geoff Kuenning

Example Plot of Residuals vs. Predicted Response © 1998, Geoff Kuenning

Example Plot of Residuals Vs. Experiment Number © 1998, Geoff Kuenning

Example Plot of Residuals Vs. Experiment Number © 1998, Geoff Kuenning

Testing for Normally Distributed Errors • As usual, do a quantile-quantile chart – Against

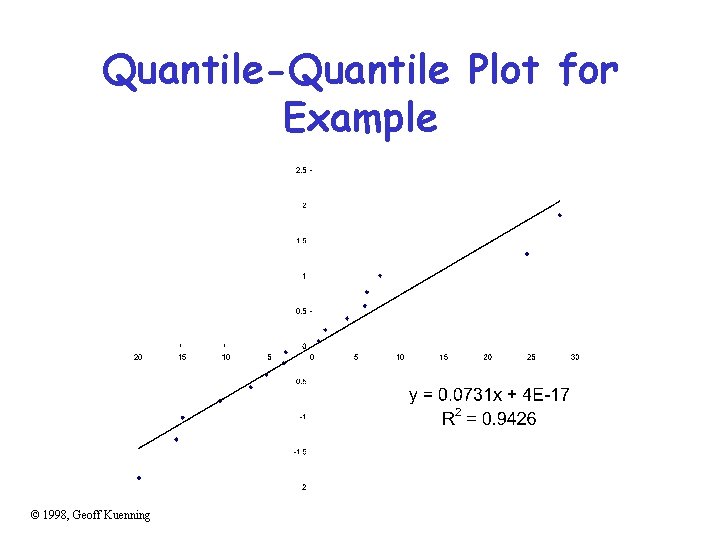
Testing for Normally Distributed Errors • As usual, do a quantile-quantile chart – Against the normal distribution • If it’s close to linear, this assumption is good © 1998, Geoff Kuenning

Quantile-Quantile Plot for Example © 1998, Geoff Kuenning

Quantile-Quantile Plot for Example © 1998, Geoff Kuenning

Assumption of Constant Variance • Checking homoscedasticity • Go back to the scatter plot

Assumption of Constant Variance • Checking homoscedasticity • Go back to the scatter plot and check for an even spread © 1998, Geoff Kuenning

The Scatter Plot, Again © 1998, Geoff Kuenning

The Scatter Plot, Again © 1998, Geoff Kuenning

Example Shows Residuals Are Function of Predictors • What to do about it? •

Example Shows Residuals Are Function of Predictors • What to do about it? • Maybe apply a transform? • To determine if we should, plot standard deviation of errors vs. various transformations of the mean • Here, dynamic load management seems to introduce greater variance – Transforms not likely to help – Probably best not to describe with regression © 1998, Geoff Kuenning

CHAPTER 5 FACTORIAL DESIGNS FACTORIAL ESSENTIALS Factorial designCHAPTER 5 FACTORIAL DESIGNS FACTORIAL ESSENTIALS Factorial design
3 way Factorial Designs Expanding factorial designs Effects3 way Factorial Designs Expanding factorial designs Effects
Factorial Designs Background n n Factorial designs areFactorial Designs Background n n Factorial designs are
Reintroduction to Factorial Designs reIntroduction to factorial designsReintroduction to Factorial Designs reIntroduction to factorial designs
Factorial Designs Chapter 11 Factorial designs Allow experimentsFactorial Designs Chapter 11 Factorial designs Allow experiments
Recursion Factorial 6 654321 Factorial 75 Factorial 75Recursion Factorial 6 654321 Factorial 75 Factorial 75
ANOVA FACTORIAL DESIGN Factorial design Factorial design anANOVA FACTORIAL DESIGN Factorial design Factorial design an
TwoLevel Factorial and Fractional Factorial Designs in BlocksTwoLevel Factorial and Fractional Factorial Designs in Blocks
Factorial Designs Factorial design a research design thatFactorial Designs Factorial design a research design that
Fractional Factorial Designs 27 Factorial Design in 8Fractional Factorial Designs 27 Factorial Design in 8
Twolevel Factorial and Fractional Factorial Designs in BlocksTwolevel Factorial and Fractional Factorial Designs in Blocks
Factorial Designs Using More Than One IV FactorialFactorial Designs Using More Than One IV Factorial
Factorial Research Hypotheses kxk BG Factorial Designs DefinitionFactorial Research Hypotheses kxk BG Factorial Designs Definition
Programmatic Research 1 Factorial Designs Kinds of FactorialProgrammatic Research 1 Factorial Designs Kinds of Factorial
True Experiments Multifactorial Designs Factorial Designs Also calledTrue Experiments Multifactorial Designs Factorial Designs Also called
Single Factor Designs vs Factorial Designs EXPERIMENTAL PSYCHOLOGYSingle Factor Designs vs Factorial Designs EXPERIMENTAL PSYCHOLOGY
NonExperimental designs Developmental designs SmallN designs Psych 231NonExperimental designs Developmental designs SmallN designs Psych 231
Experimental Group Designs Group Designs Simple Group DesignsExperimental Group Designs Group Designs Simple Group Designs
NonExperimental designs Developmental designs SmallN designs Psych 231NonExperimental designs Developmental designs SmallN designs Psych 231
NonExperimental designs Developmental designs SmallN designs Psych 231NonExperimental designs Developmental designs SmallN designs Psych 231
NonExperimental designs Developmental designs SmallN designs Psych 231NonExperimental designs Developmental designs SmallN designs Psych 231
QUASIEXPERIMENTAL DESIGNS SMALL N DESIGNS CORRELATIONAL DESIGNS WeekQUASIEXPERIMENTAL DESIGNS SMALL N DESIGNS CORRELATIONAL DESIGNS Week
Different Conceptual Designs Different Conceptual Designs Designs forDifferent Conceptual Designs Different Conceptual Designs Designs for
Used Ep Used Esxsy Used sxsy Used EpUsed Ep Used Esxsy Used sxsy Used Ep