Gene Expression Based Tumor Classification Using Biologically Informed

Gene Expression Based Tumor Classification Using Biologically Informed Models Claudio Lottaz und Rainer Spang Computational Diagnostics Group Max Planck Institute for Molecular Genetics, Berlin ISI 2003 Berlin

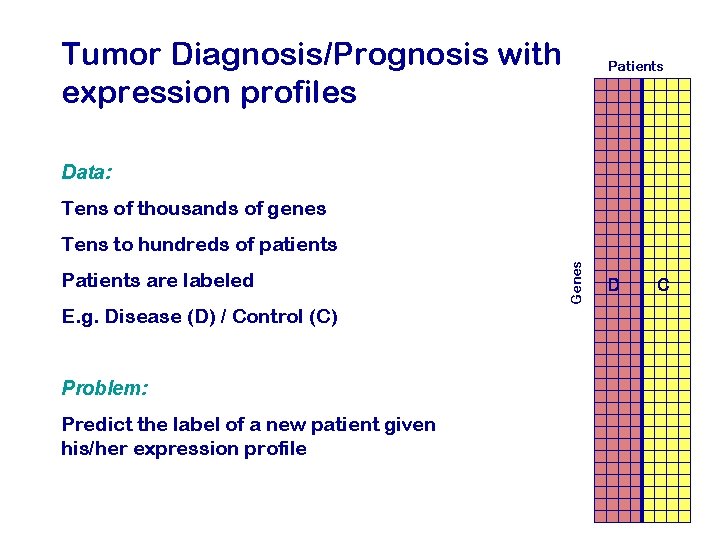
Tumor Diagnosis/Prognosis with expression profiles Patients Data: Tens of thousands of genes Patients are labeled E. g. Disease (D) / Control (C) Problem: Predict the label of a new patient given his/her expression profile Genes Tens to hundreds of patients D C

Statistical Context: Learning Theory High dimensional models overfitting problems Additional constraints Regularized Multivariate Models What are these constraints? -A small maximal number of genes allowed in the model (Variable Selection, Sparse Models) - Likelihood penalties, - Informative priors, - Large Margins,

Frustrations • Falsely predicted patients • Questionable Labels • Genes that make no sense in the context • Secondary and tertiary effects are more prominent then causal molecular mechanisms

Implicit assumptions of standard approaches The patient groups are seen as molecular homogenous groups Genes are anonymous variables: x 1, …, xn

Our approach: 1. Sub-class finding instead of global class prediction 2. Use of functional annotations of genes Molecular Symptoms

Global class prediction vs. Subclass finding Global class prediction: Find a molecular signature that separates D from C and generalizes to new patients D C D‘ DD‘ C Subclass finding: Find a Subclass D‘ ½D and a molecular signature that separates D‘ from C We call this signature a molecular symptom associated to D

Molecular symptoms • High specificity and sub-optimal sensitivity • partially supervised • Molecular properties that are (almost) unique to the disease group, but do not need to be present in all patients having the disease • Novel stratification of patients • Hidden molecular sub-entities • There are in general many molecular symptoms associated to a disease • One patient can have several molecular symptoms

Exploiting functional annotations of genes A posteriori use of functional annotations Data Statistical Analysis Functional Annotations A priori use of functional annotations ( suggested here ) Data Statistical Analysis Functional Annotations

What are we looking for? DNA Repair D‘ 1 D‘ 2 Apoptosis C Cell Proliferation HOX Genes D‘ 3 D‘ 4

Functional grouping of genes using Gene Ontologies (GO) GO is a database of terms for genes n Known genes are annotated to the terms n Terms are connected as a directed acyclic graph n Levels represent specifity of the terms n

The whole thing at a glance GO contains three different subontologies: –Molecular function –Biological process –Cellular component

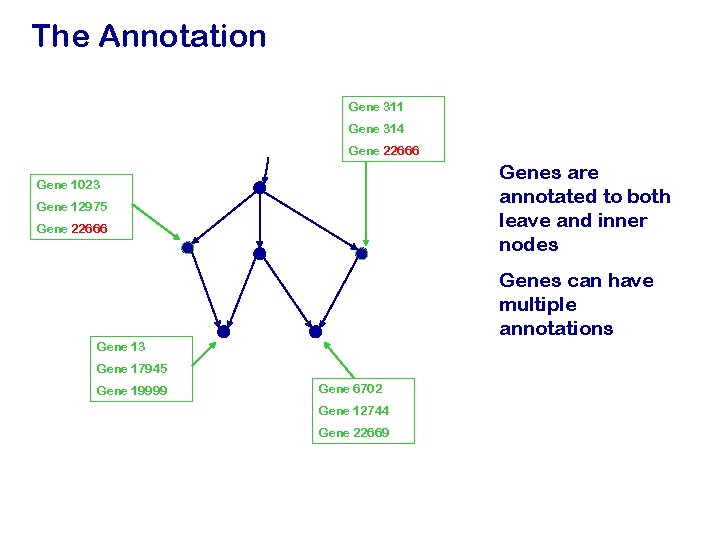
The Annotation Gene 311 Gene 314 Gene 22666 Genes are annotated to both leave and inner nodes Gene 1023 Gene 12975 Gene 22666 Genes can have multiple annotations Gene 13 Gene 17945 Gene 19999 Gene 6702 Gene 12744 Gene 22669

Augmented Ontology Gene 1023 Gene 12975 Gene 22666

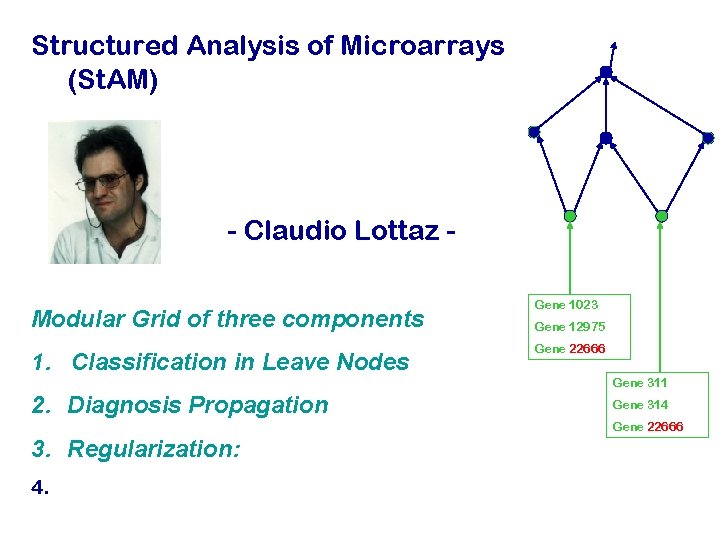
Structured Analysis of Microarrays (St. AM) - Claudio Lottaz Modular Grid of three components 1. Classification in Leave Nodes Gene 1023 Gene 12975 Gene 22666 Gene 311 2. Diagnosis Propagation Gene 314 Gene 22666 3. Regularization: 4.

1. Classification in the leave nodes by Shrunken centroid classification: PAM (Tibshirani et al 2002) DLDA-like Discrimination Discriminant function via the distance to the shrunken class centroids d(C), d(D) Regularization: Variable selection via centroid shrinkage Class Probabilities:

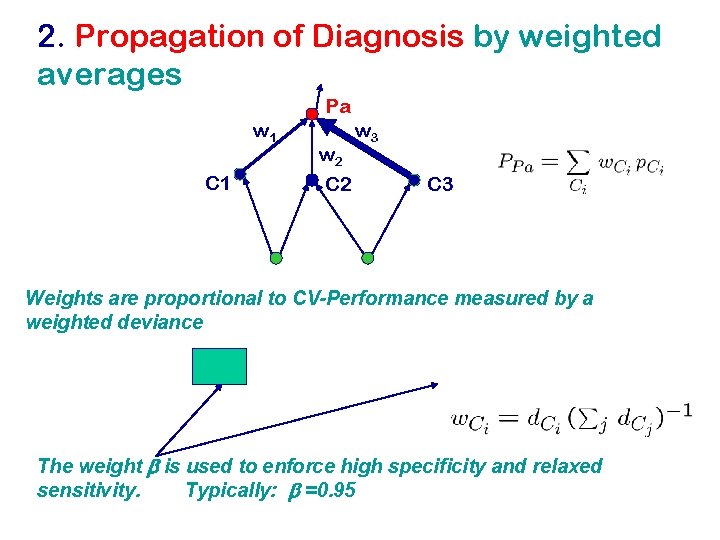
2. Propagation of Diagnosis by weighted averages Pa w 1 C 1 w 2 C 2 w 3 C 3 Weights are proportional to CV-Performance measured by a weighted deviance The weight b is used to enforce high specificity and relaxed sensitivity. Typically: b =0. 95

3. Regularization by graph shrinkage To get rid of uninformative branches of the Gene Ontology, we shrink the weights in the progression step by a constant D D is chosen by crossvalidation

Redundancy of a shrunken graph For two nodes we define the distance: . . . which reflects the probability of an inconsistent diagnosis For a single node we define its redundancy after shrinkage: . . . where KD is the set of all remaining nodes in the graph after shrinkage For a shrunken GO graph, we define its redundancy:

Expression data from a leukemia study Yeoh et al. , Cancer Cell 2002 Study on acute lymphoblastic leukaemia (ALL) 327 patients 12625 genes (Affymetrix HGU 95 Av 2) My focus in this talk: MLL – ( ) vs. Others Objective: Diagnosis of cytogenetic subtypes of ALLs: 20 MLL - ( ) 27 E 2 A-PBX 1 15 BCR-ABL 79 TEL-AML 1 87 Hyperdiploid 7 Hypodiploid 29 Pseudodiploid 18 nomal (B-cell ALL) 43 T-ALL

Training and Test Disease group: ( MLL positive ALL ) Control group : ( other types of ALL ) Trainings – Test data (2/3 – 1/3 of both Disease and Control cases, randomly split) All model selection steps are part of the training !!! They are performed using CV of only the trainings data. - Centroid shrinkage in the leave nodes - Deviances for the propagation weights - Graph shrinkage

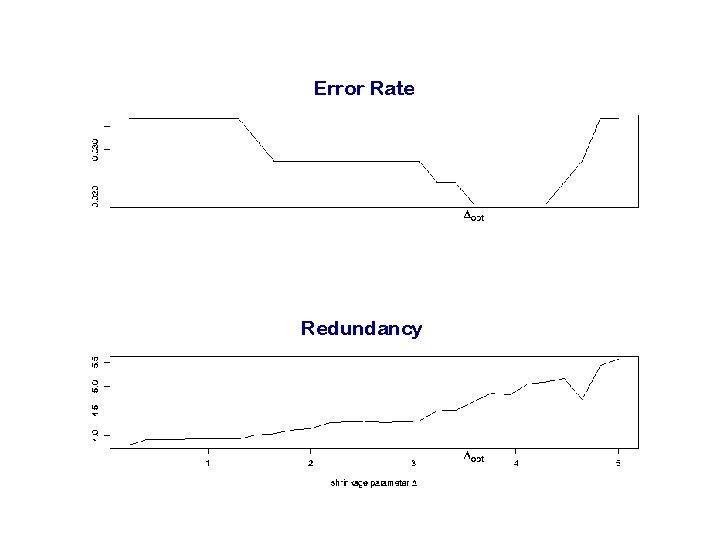
Error Rate Redundancy

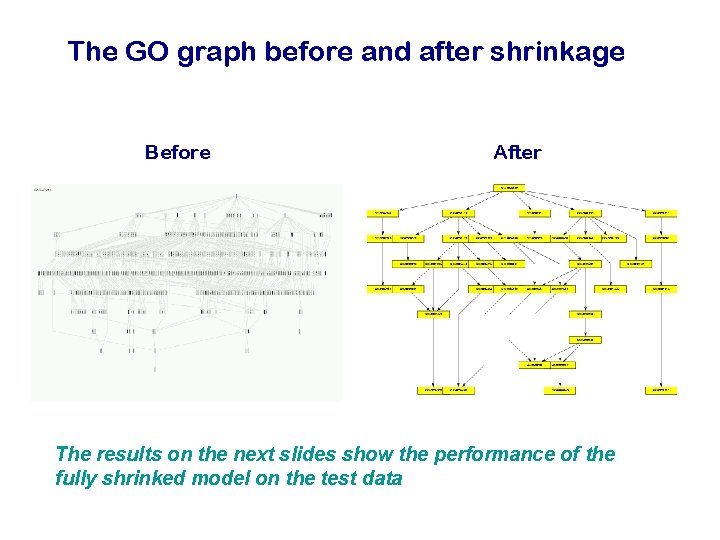
The GO graph before and after shrinkage Before After The results on the next slides show the performance of the fully shrinked model on the test data

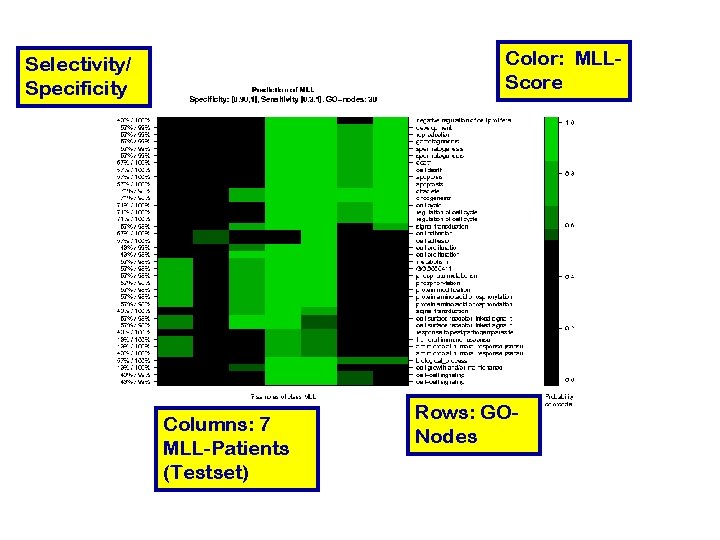
Color: MLLScore Selectivity/ Specificity Columns: 7 MLL-Patients (Testset) Rows: GONodes

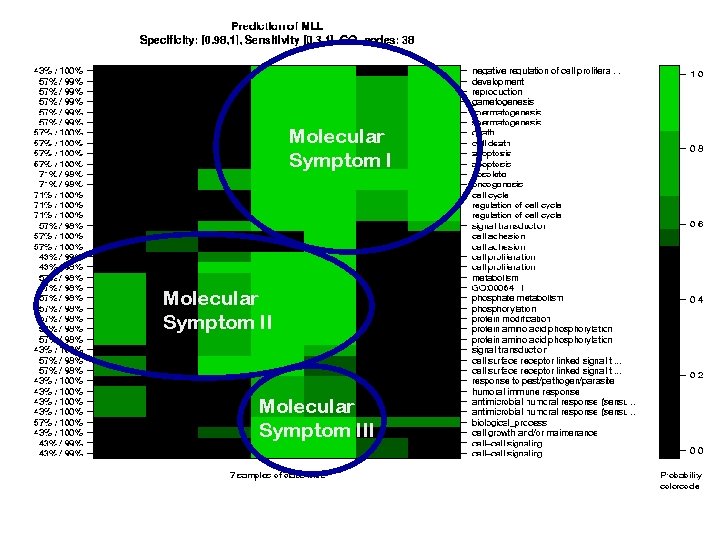
Molecular Symptom III

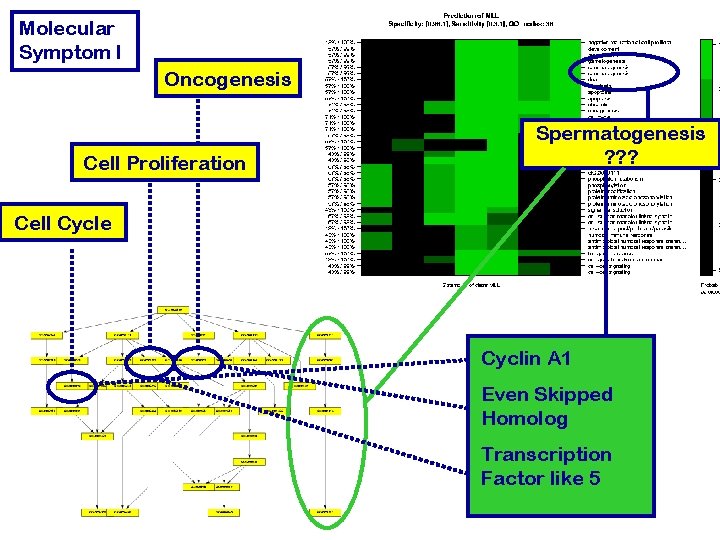
Molecular Symptom I Oncogenesis Cell Proliferation Spermatogenesis ? ? ? Cell Cycle Cyclin A 1 Even Skipped Homolog Transcription Factor like 5

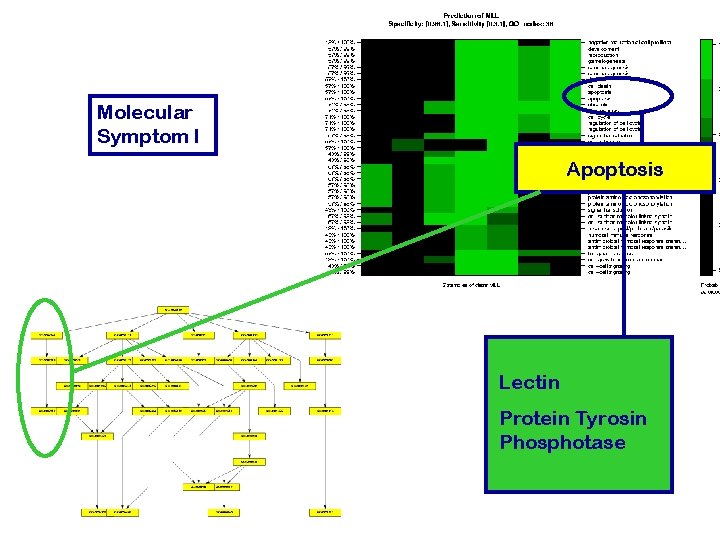
Molecular Symptom I Apoptosis Lectin Protein Tyrosin Phosphotase

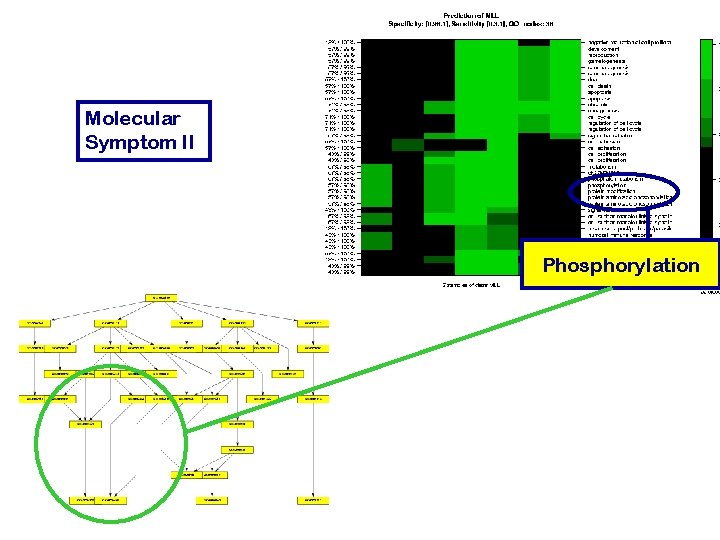
Molecular Symptom II Phosphorylation

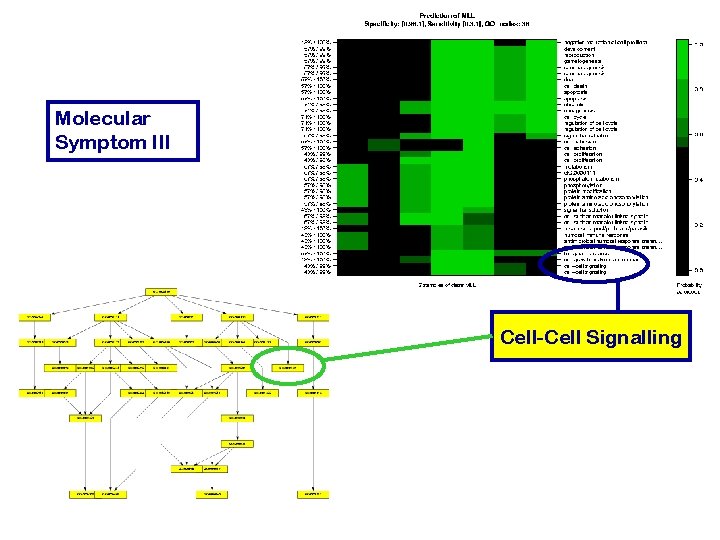
Molecular Symptom III Cell-Cell Signalling

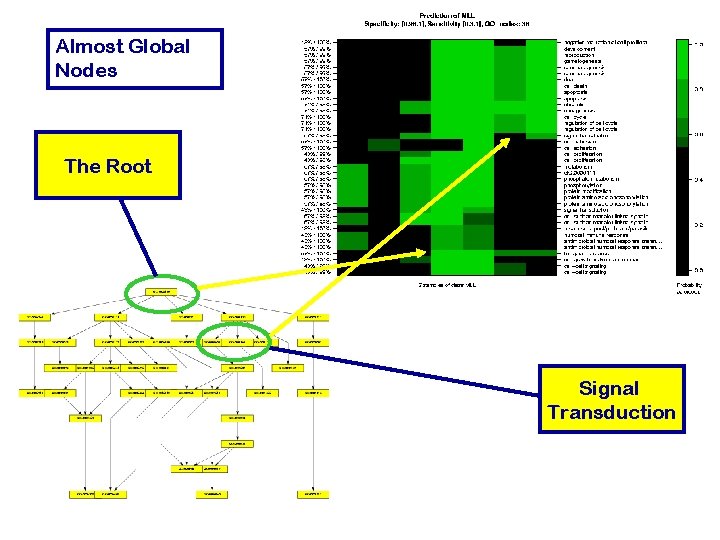
Almost Global Nodes The Root Signal Transduction

Claudio Lottaz R-code St. AM Structured Analysis of Microarrays Julie Floch Java Application for browsing St. AM output

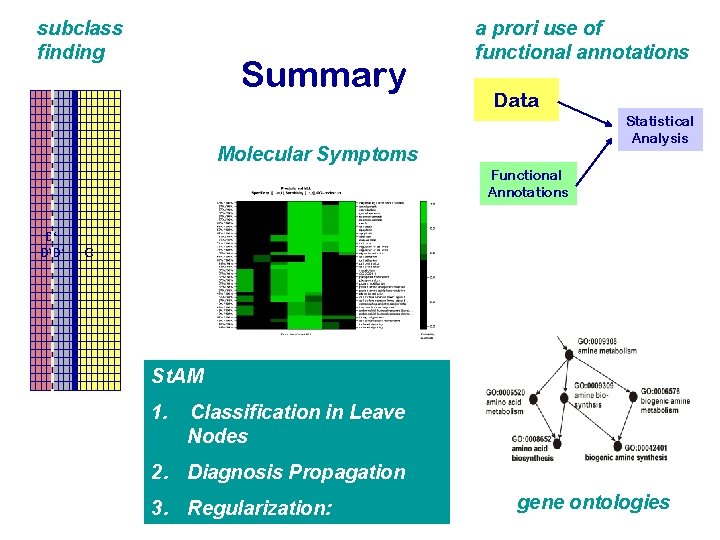
subclass finding Summary a prori use of functional annotations Data Statistical Analysis Molecular Symptoms Functional Annotations D‘ DD‘ C St. AM 1. Classification in Leave Nodes 2. Diagnosis Propagation 3. Regularization: gene ontologies