Gebze Technical University Department of Architecture MAT 119

Gebze Technical University Department of Architecture MAT 119 Asst. Prof. Ferhat PAKDAMAR (Civil Engineer) N Blok 1 -17 pakdamar@gtu. edu. tr Fall – 2016_2017 Week 2

Osmanlı Geometri - Üç dılı birbirine müsavi müselleslerin irtifaını nasıl bulurlar. - Dılın murabbaından, dılın nısfının murabbaını nakşeder, kök murabbaını alırsın. -Kaim zaviyeli müselleste, bir kaim zaviyenin karşısındaki kaim dılın kaim vetere nispetine o hadde zaviyenin nesi derler - Ceybi derler

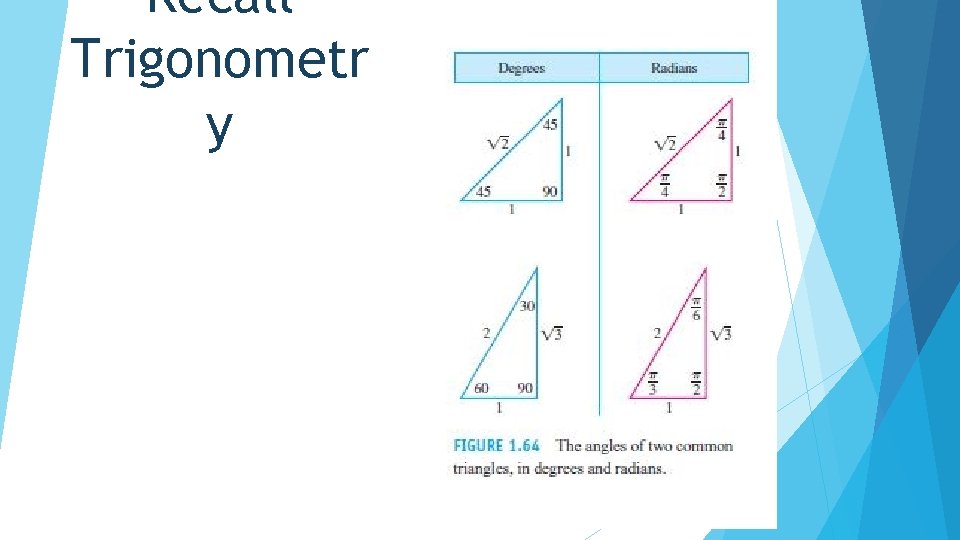
Recall Trigonometr y

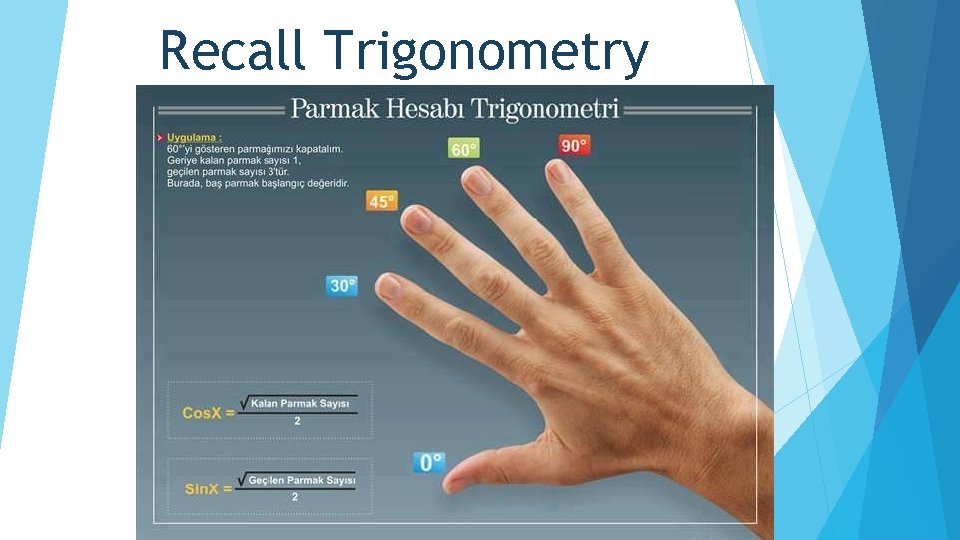
Recall Trigonometry

RADYAN

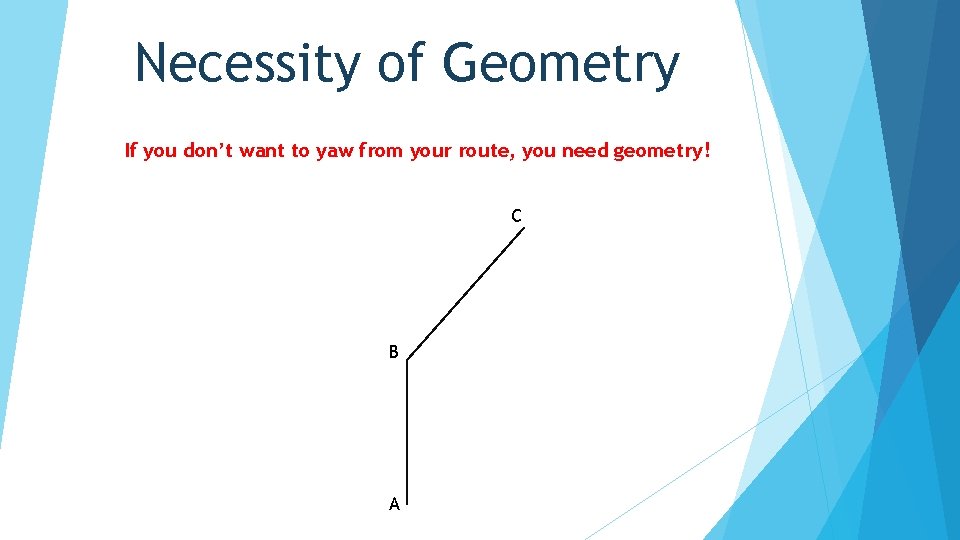
Necessity of Geometry If you don’t want to yaw from your route, you need geometry! C B A

History of Geometry (from the Ancient Greek: γεωμετρία; geo- "earth", -metron "measurement") is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer. Geometry arose independently in a number of early cultures as a body of practical knowledge concerning lengths, areas, and volumes, with elements of formal mathematical science emerging in the West as early as Thales(6 th Century BC). By the 3 rd century BC, geometry was put into an axiomatic form by Euclid, whose treatment— Euclidean geometry—set a standard for many centuries to follow. Archimedes developed ingenious techniques for calculating areas and volumes, in many ways anticipating modern integral calculus. The field of astronomy, especially as it relates to mapping the positions of stars and planets on the celestial sphere and describing the relationship between movements of celestial bodies, served as an important source of geometric problems during the next one and a half millennia.

Basics of Geometry - Points, Lines & Planes - Segments, Rays & Lines - Distance Between Points - Distance Formula in “n” Dimensions - Angles Types of Angles

Types, methodologies and terminologies of Geometry Absolute geometry Affine geometry Algebraic geometry Analytic geometry Archimedes' use of infinitesimals Birational geometry Complex geometry Combinatorial geometry Computational geometry Conformal geometry Constructive solid geometry Contact geometry Convex geometry Descriptive geometry Differential geometry Digital geometry Discrete geometry Distance geometry Elliptic geometry Enumerative geometry Epipolar geometry Finite geometry Fractal geometry Geometry of numbers Hyperbolic geometry Incidence geometry Information geometry Integral geometry Inversive ring geometry Klein geometry Lie sphere geometry Non-Euclidean geometry Numerical geometry Ordered geometry Parabolic geometry Plane geometry Projective geometry Quantum geometry Reticular geometry Riemannian geometry Ruppeiner geometry Spherical geometry Symplectic geometry Synthetic geometry Systolic geometry Taxicab geometry Toric geometry Transformation geometry Tropical geometry …

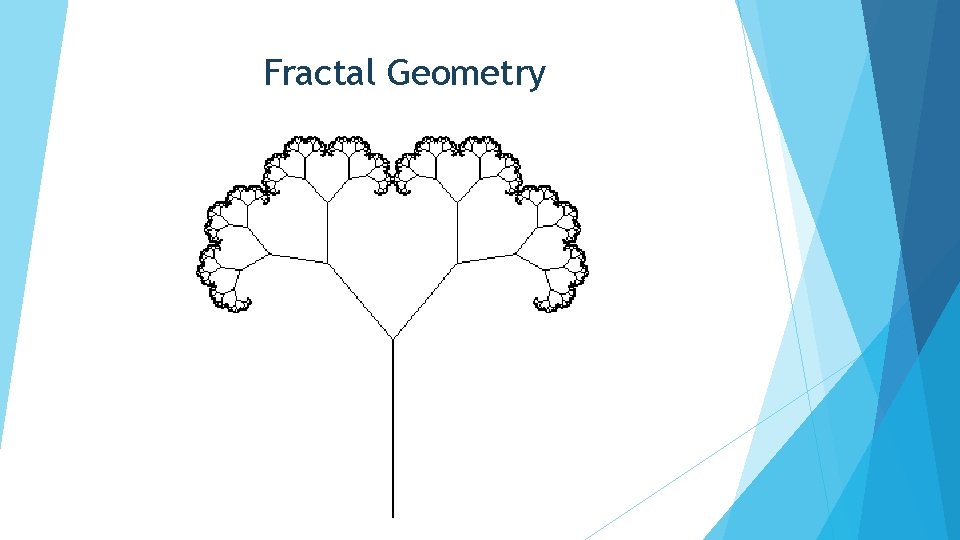
Fractal Geometry 1 A geometric figure that appears irregular at all scales of length, e. g. a fern 2 A geometric figure which has a Hausdorff dimension which is greater than its topological dimension 3 Having the form of a fractal 4 A mathematically generated pattern that is endlessly complex Fractal patterns often resemble natural phenomena in the way they repeat elements with slight variations each time A kind of image that is defined recursively, so that each part of the image is a smaller version of the whole 6 A fractal is a shape where self-similarity dimension is greater than topological dimension 5 A geometric entity characterized by self-similarity (see figure 2): the whole entity is similar to a smaller portion of itself, but has a higher level of recursion (see recursion) Therefore, it can usually 7 be represented by a recursive definition When using a fractal to represent a physical object, some degree of randomness is usually added to make the image more realistic groups that have broken dimensions so that each one looks like an exact copy of the second (like the 8 Mandelbrot group in Mathematics); (In Computers) geometric shapes that have interesting contour lines 9 A geometric figure that repeats itself under several levels of magnification, a shape that appears irregular at all scales of length, e. g. a fern 10 A geometric figure, built up from a simple shape, by generating the same or similar changes on successively smaller scales; it shows self-similarity on all scales

Fractal Geometry Every fractal is a pattern but every pattern is not a fractal A pattern can be a fractal with these rules 1 - Pattern must be scaled 2 - Previous form must be contained 3 - Must proceed according to a specific rule Pattern? Fractal? It is a pattern. Because Next shape can be predicted Not a fractal Because Shape is not scaled

Fractal Geometry Every fractal is a pattern but every pattern is not a fractal A pattern can be a fractal with these rules 1 - Pattern must be scaled 2 - Previous form must be contained 3 - Must proceed according to a specific rule Pattern? Fractal? It is a pattern. Because Next shape can be predicted Not a fractal Because Next shape is not encapsulate the previous

Fractal Geometry Every fractal is a pattern but every pattern is not a fractal A pattern can be a fractal with these rules 1 - Pattern must be scaled 2 - Previous form must be contained 3 - Must proceed according to a specific rule Pattern? Fractal? It is a pattern and a fractal

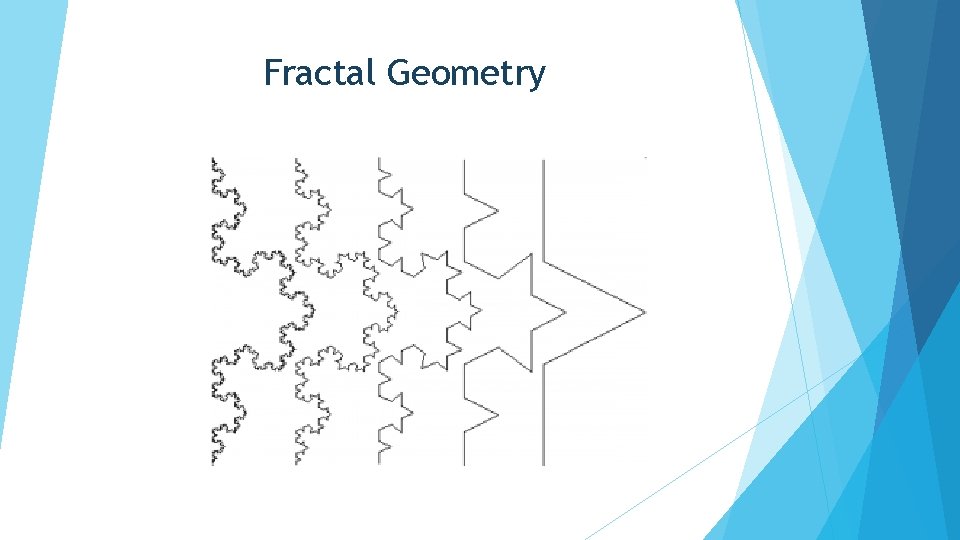
Fractal Geometry

Fractal Geometry

Fractal Geometry

Fractal Geometry

Dimension of a Fractal (Hausdorff)

Sample Fractal Figures These figures are very important for midterm exam and Homeworks !

Basics of Geometry - Points, Lines & Planes - Segments, Rays & Lines - Distance Between Points - Distance Formula in “n” Dimensions - Angles Types of Angles