GE 177 b Appendix Construction of balanced crosssections

GE 177 b - Appendix: Construction of balanced cross-sections I. III. IV. Construction of cross-sections Balancing a cross section Fault-related folds Growth and pre-growth strata

I. Construction of a cross-section • Define the plane section (in general vertical but not necessarily). • Determine topographic profile (without any vert. exaggeration) • Plot geologic data (measurements of strike and dip; intersections of stratigraphic contacts; faults). • Extrapolate and interpolate data. (cf Suppe, Principles of Structural Geology, 1985)

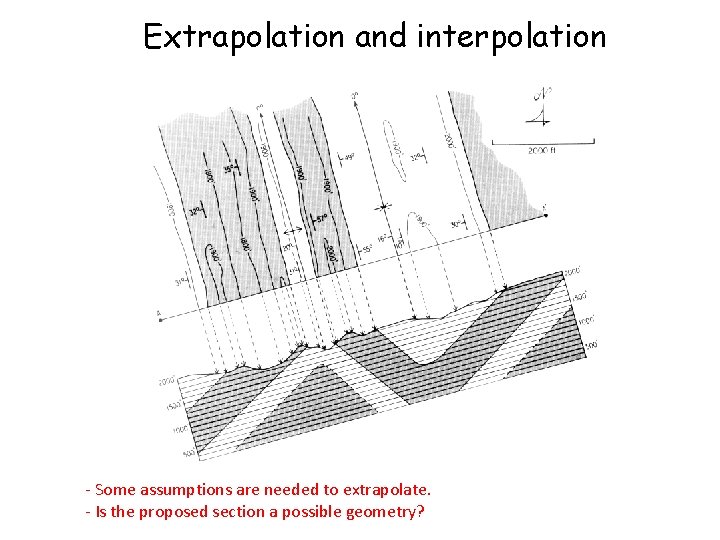
Extrapolation and interpolation - Some assumptions are needed to extrapolate. - Is the proposed section a possible geometry?

II. Constructing a balanced crosssection from the kink method • Assemble data (surface and subsurface observations) • Define dip domains, positions and dip angles of axial surface. • Extrapolate at depth by trials and errors. (you will need an eraser, experience will help). • Test that the section is indeed retrodeformable.

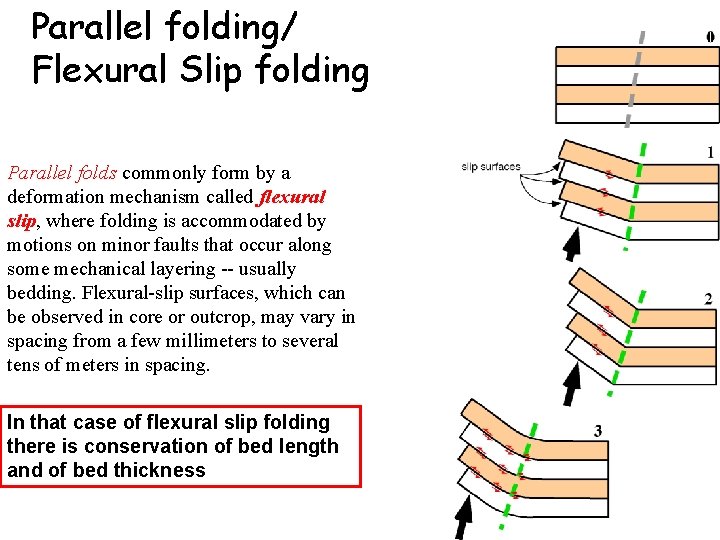
Parallel folding/ Flexural Slip folding Parallel folds commonly form by a deformation mechanism called flexural slip, where folding is accommodated by motions on minor faults that occur along some mechanical layering -- usually bedding. Flexural-slip surfaces, which can be observed in core or outcrop, may vary in spacing from a few millimeters to several tens of meters in spacing. In that case of flexural slip folding there is conservation of bed length and of bed thickness

The Kink method for a parallel fold… The kink method is based on the assumption of flexural slip folding in the limit where dip angles varie only across axial surfaces (it is equivalent to the Busk method with infinite curvature within dip domains and zero curvature within axial surface. γ -the axial surface bisects the angle between the fold limbs Axial angle : γ γ

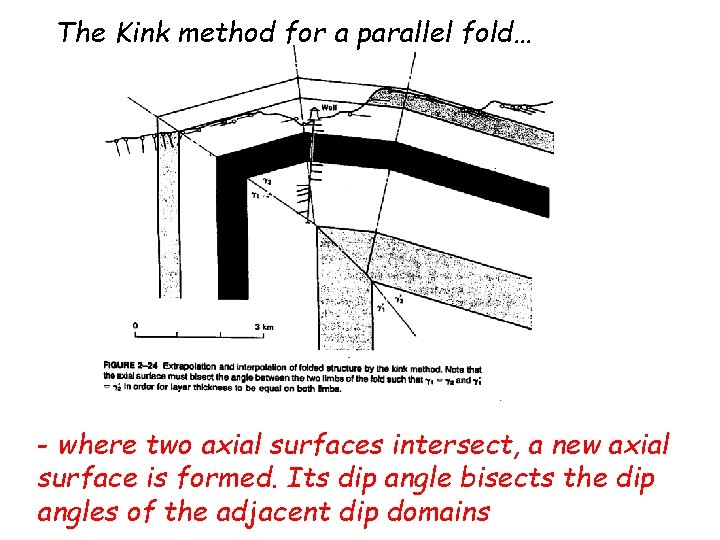
The Kink method for a parallel fold… - where two axial surfaces intersect, a new axial surface is formed. Its dip angle bisects the dip angles of the adjacent dip domains

The Kink method for a parallel fold… - Dip angles are constant within dip domains separated by axial surfaces. -the axial surface bisects the angle between the fold limbs

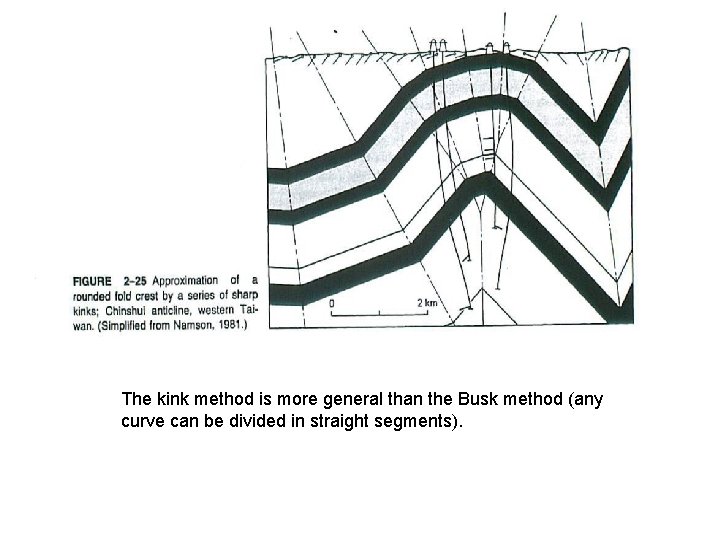
The kink method is more general than the Busk method (any curve can be divided in straight segments).

Curvimetric Shortening & planimetric shortening Curvimetric Shortening: Sc= Lc-l Planimetric shortening: Sa=Asr/h Structural relief: Asr Undeformed depth of decollement below bed: h Area of Shortening: A Conservation of area implies: A=Asr= Sc*h. NB: Both quantities refer to a particular bed.

Curvimetric Shortening & planimetric shortening Curvimetric Shortening: Sc= Lc-l Structural relief: Asr Depth of decollement below bed: h Area of Shortening: A Conservation of area implies: A=Asr= Sc*h Planimetric shortening: A/h=Asr/h Conservation of area and bed length implies : - curvimetric shortening = planimetric shortening - Asr should increase linearly with elevation above decollement.

Sc= 0, 95 km Asr/h=2. 6 km Sc= 0, 95 km Asr/h=0. 95 km If area and bed length is preserved during folding then b is the most plausible solution …or a is correct but some diapirism is involved

Equality of curvilinear and planimetric shortening can be used to either check the section or predict the depth to the decollement. Asr= Sc*h

Structural relief: Asr Equality of curvilinear and planimetric shortening can be used to either check the section or predict the depth to the decollement.

Structural relief: Asr Equality of curvilinear and planimetric shortening can be used to either check the section or predict the depth to the decollement. NB: Be careful with the possibility of diapirism

The Move software Midland Valley Ltd. MOVE is the core product of the Move Suite providing a powerful structural modelling environment. Move provides data integration, 2 D cross-section construction and 3 D model building and is the base for the specialist structural modules for 2 D and 3 D kinematic, geomechanical, fracture and sediment modelling. MOVE 2 D- removes deformation to restore the present day interpretation to its un-deformed state, adhering to line length and area balancing structural geology principles and taking into account the importance of geological time and its impact on the structure of today. MOVE 3 D

III. Fault-related folds • Fault-bend folds • Fault-tip folds

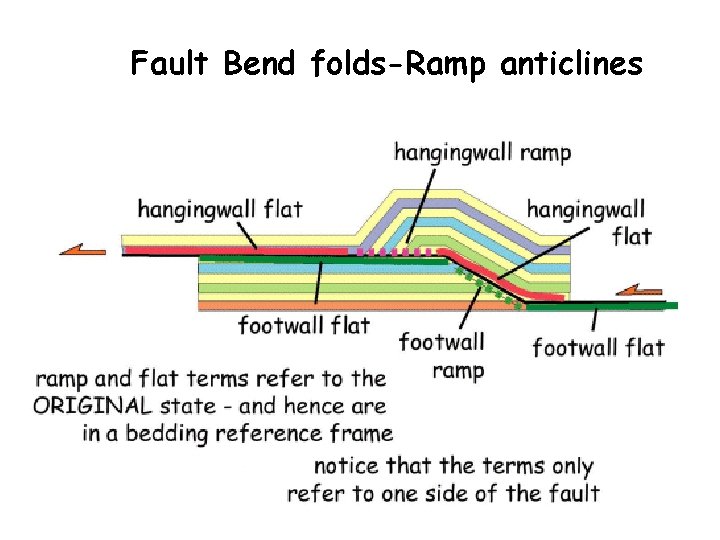
Fault Bend folds-Ramp anticlines Could also relate to fault propagation

Folds related to blind thrust faults Detachment folds Fault-tip folds Fault-detachment folds evolve into fault-tip folds and fault –bend folds

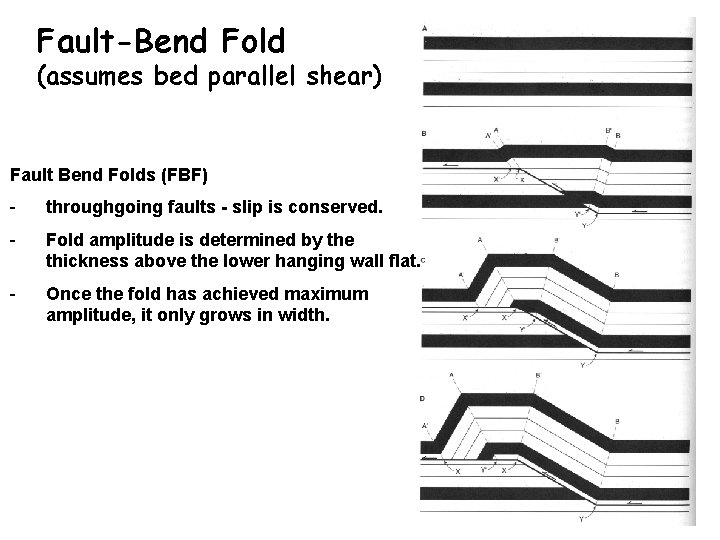
Fault-Bend Fold (assumes bed parallel shear) Fault Bend Folds (FBF) - throughgoing faults - slip is conserved. - Fold amplitude is determined by the thickness above the lower hanging wall flat. - Once the fold has achieved maximum amplitude, it only grows in width.

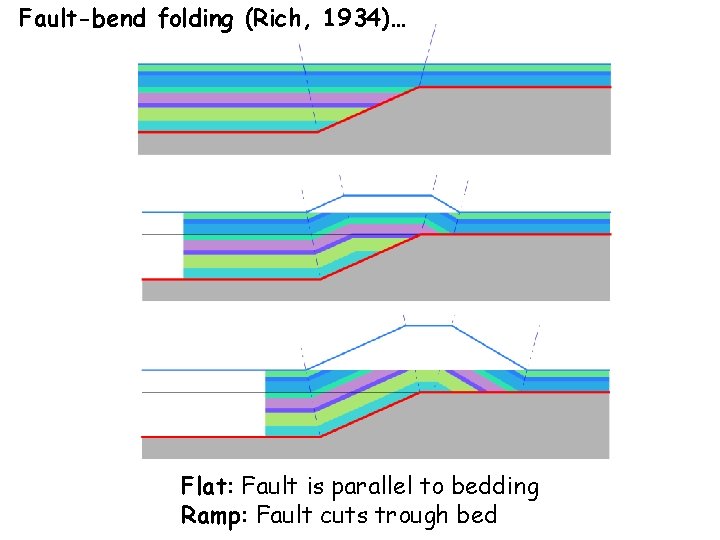
Fault-bend folding (Rich, 1934)… Flat: Fault is parallel to bedding Ramp: Fault cuts trough bed

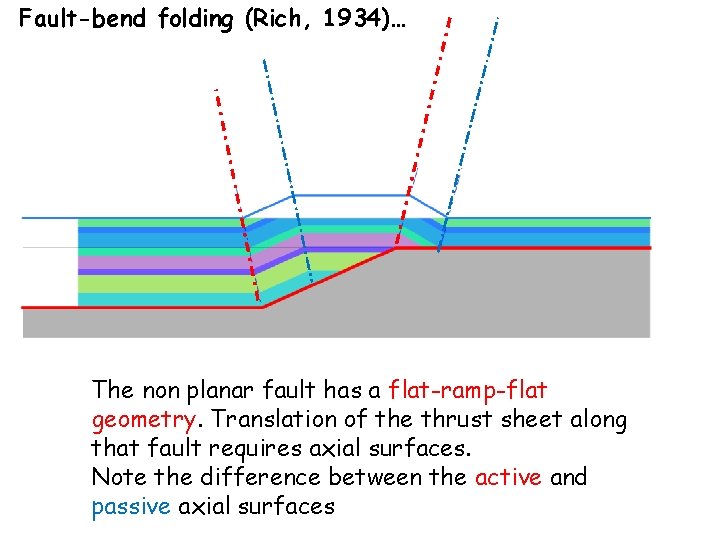
Fault-bend folding (Rich, 1934)… The non planar fault has a flat-ramp-flat geometry. Translation of the thrust sheet along that fault requires axial surfaces. Note the difference between the active and passive axial surfaces

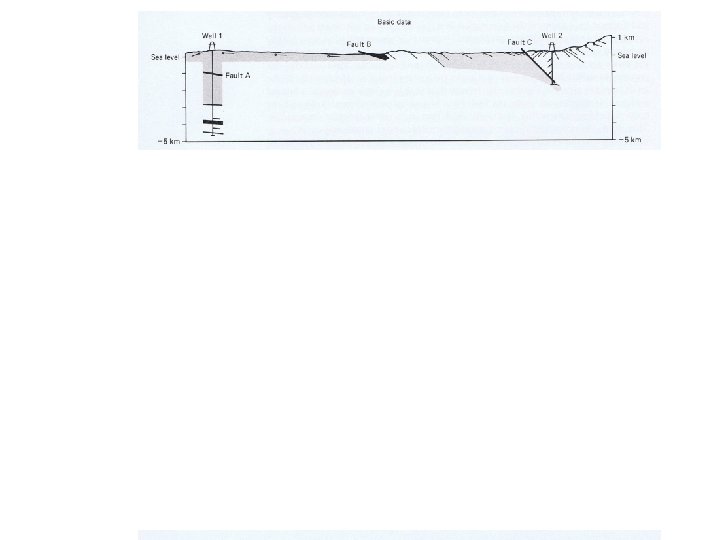
Decollement

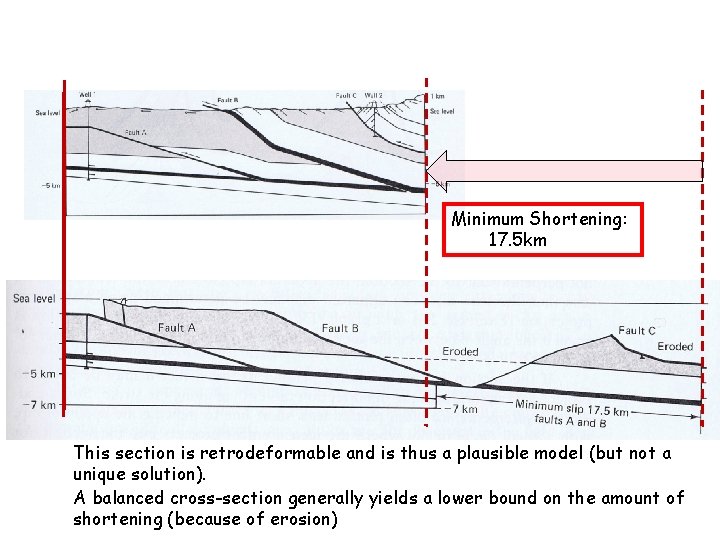
Minimum Shortening: 17. 5 km This section is retrodeformable and is thus a plausible model (but not a unique solution). A balanced cross-section generally yields a lower bound on the amount of shortening (because of erosion)

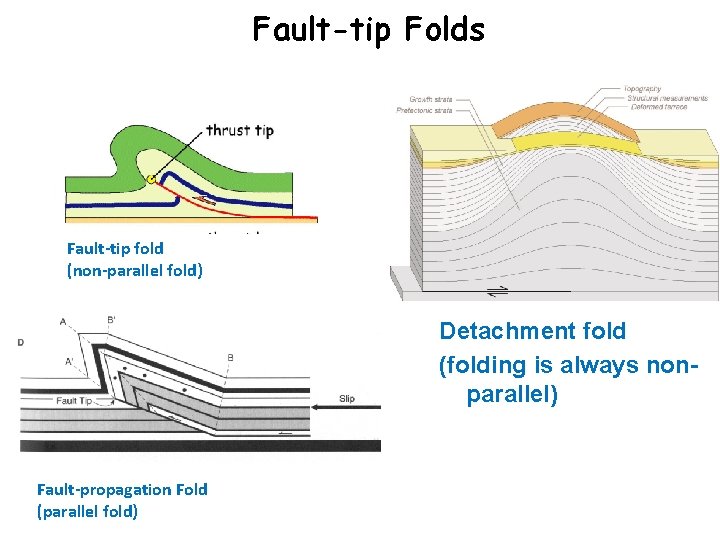
Fault-tip Folds Fault-tip fold (non-parallel fold) Detachment fold (folding is always nonparallel) Fault-propagation Fold (parallel fold)

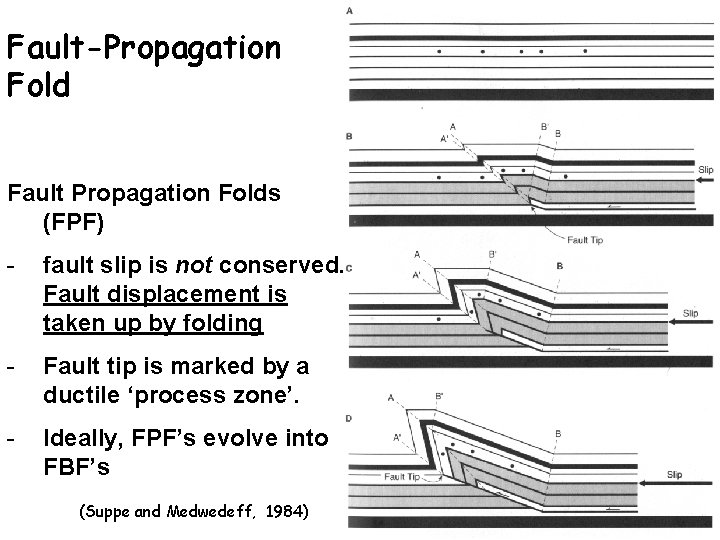
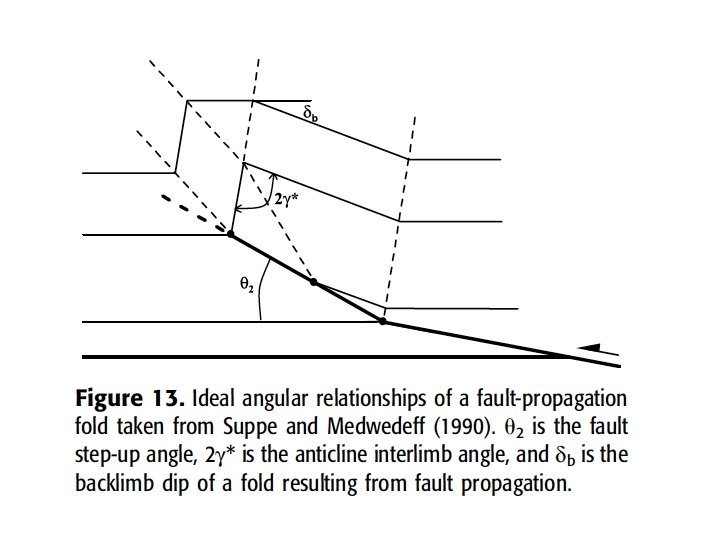
Fault-Propagation Fold Fault Propagation Folds (FPF) - fault slip is not conserved. Fault displacement is taken up by folding - Fault tip is marked by a ductile ‘process zone’. - Ideally, FPF’s evolve into FBF’s (Suppe and Medwedeff, 1984)

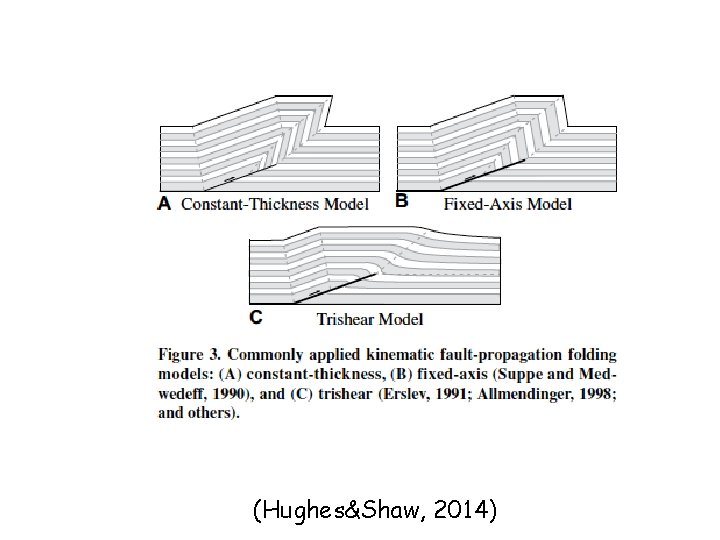
(Hughes&Shaw, 2014)

IV. Growth and pre-growth strata • The assumption of beds with constant thickness holds generally for ‘pre-growth’ strata. Syntectonic deposition will induce lateral variations of bed thickness. Such strata are called ‘growth strata’.

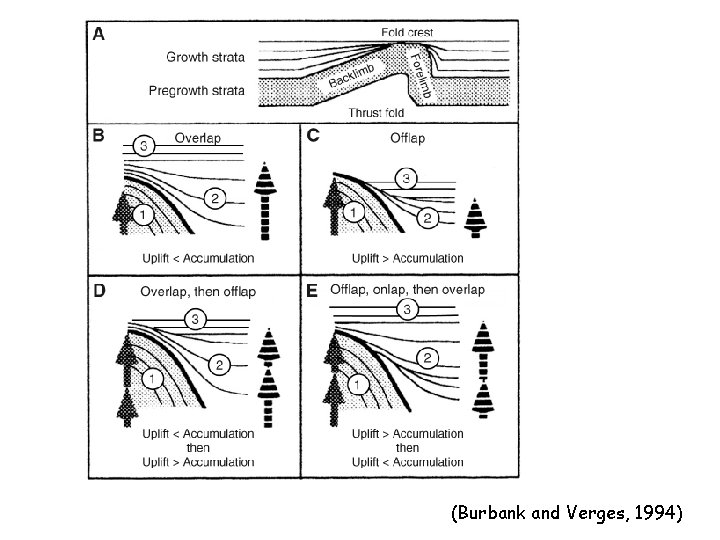
(Burbank and Verges, 1994)

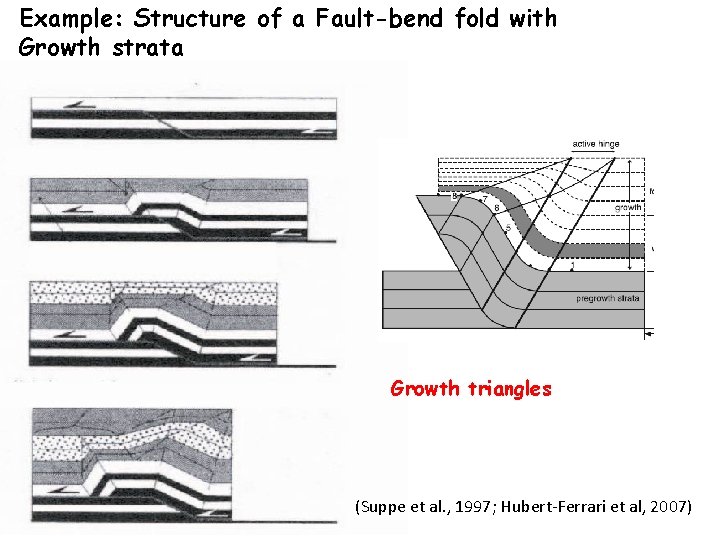
Example: Structure of a Fault-bend fold with Growth strata Growth triangles (Suppe et al. , 1997; Hubert-Ferrari et al, 2007)

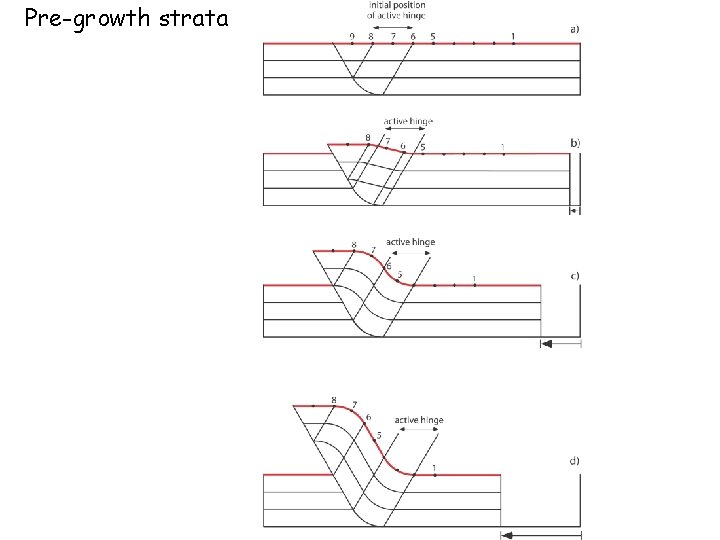
Pre-growth strata

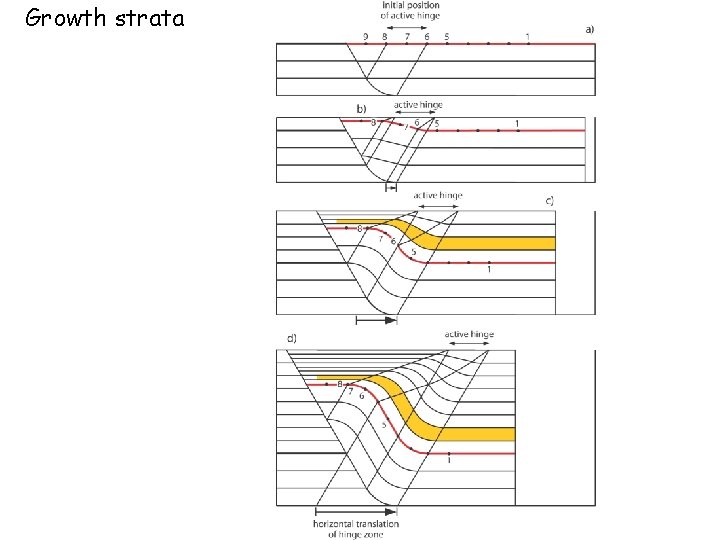
Growth strata