GCSE Statistics Probability Venn Diagrams A little about

GCSE Statistics Probability Venn Diagrams

A little about John Venn and Venn diagrams before we start. . John Venn was born in 1834 at Hull, Yorkshire. His mother, Martha Sykes, came from Swanland, near Hull. Venn's main area of interest was logic and he published three texts on the subject. The second was Symbolic Logic in which he introduced the Venn diagrams in 1881. (4 August 1834 – 4 April 1923),

A Venn diagram is a way of representing a sample space. Each region of the diagram represents the number of a different set of data.

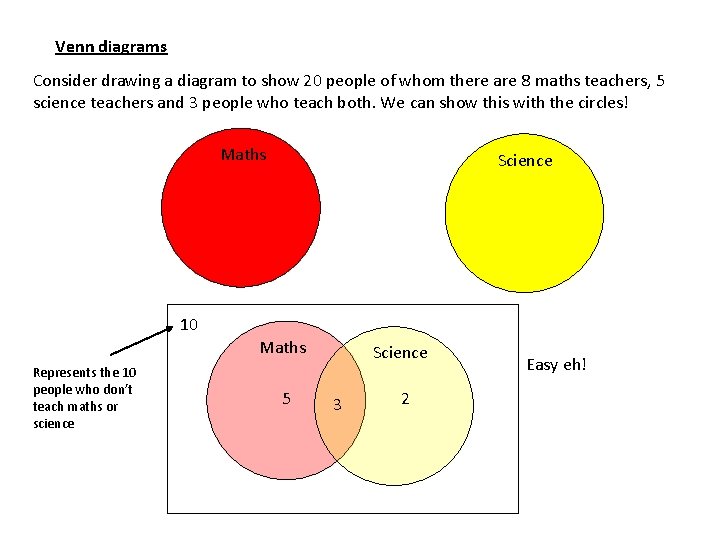
Venn diagrams Consider drawing a diagram to show 20 people of whom there are 8 maths teachers, 5 science teachers and 3 people who teach both. We can show this with the circles! Maths Science 10 Maths Represents the 10 people who don’t teach maths or science 5 Science 3 2 Easy eh!

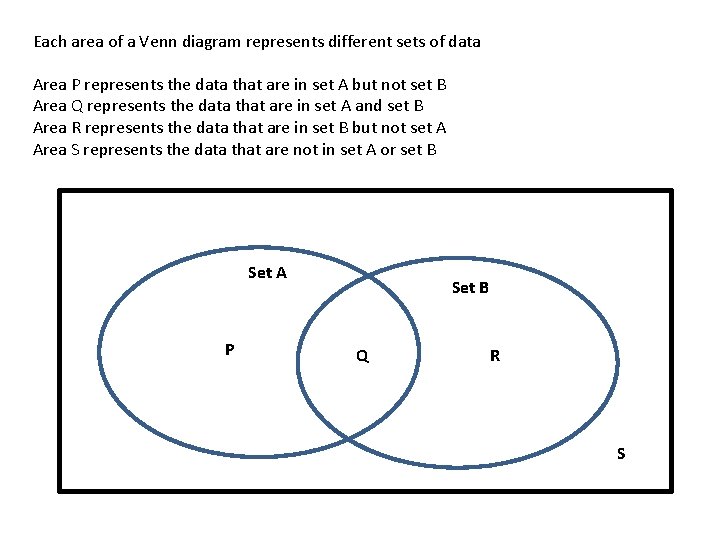
Each area of a Venn diagram represents different sets of data Area P represents the data that are in set A but not set B Area Q represents the data that are in set A and set B Area R represents the data that are in set B but not set A Area S represents the data that are not in set A or set B Set A P Set B Q R S

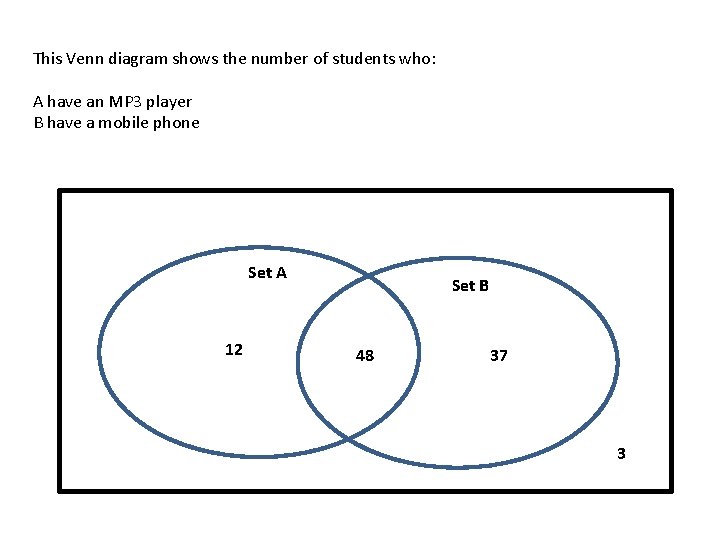
This Venn diagram shows the number of students who: A have an MP 3 player B have a mobile phone Set A 12 Set B 48 37 3

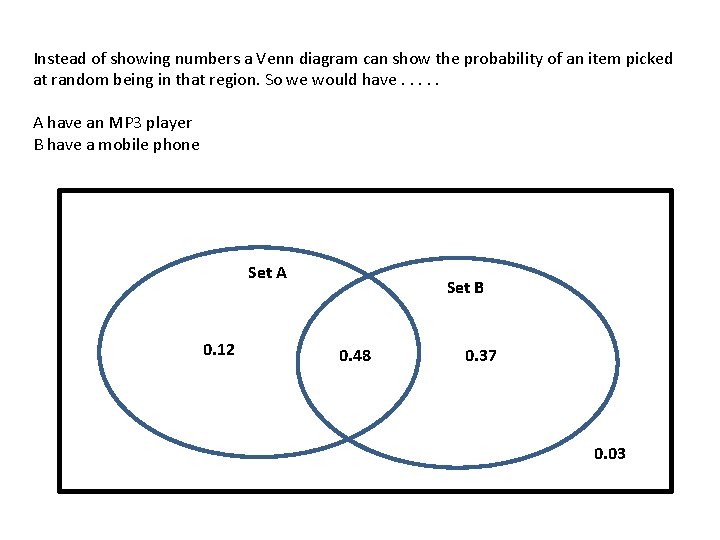
Instead of showing numbers a Venn diagram can show the probability of an item picked at random being in that region. So we would have. . . A have an MP 3 player B have a mobile phone Set A 0. 12 Set B 0. 48 0. 37 0. 03

A health trust does a survey to see how many of it’s hospital beds have access to a radio and/or a television. It finds that 21% have access to televisions only, 12% have access to radios only and 2% have access to neither. a. Draw a Venn diagram to represent this data b. Find the probability that a bed chosen at random will have access to a radio or a television but not both. c. Find the probability that a bed chosen at random will not have access to a television. d. Given that a patient is in a bed with access to a radio, what is the probability that the bed also has access to a television? Exam hints • Draw the rectangle round the circles (it represents the universal set ) • Don’t forget those that are in neither set • To change to probabilities divide by the total number in the diagram • The total of probabilities should add up to 1

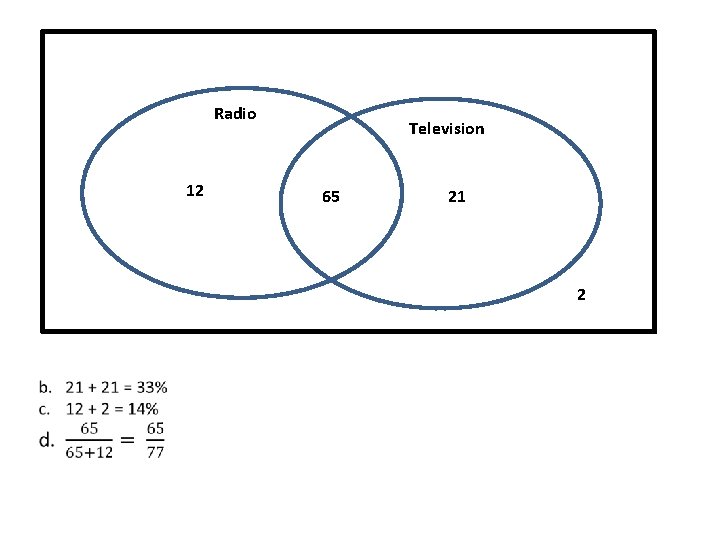
Radio 12 Television 65 21 2

Your turn Exercise 7 F page 264