GCSE Statistics Probability Experimental Probability 1 0 9

GCSE Statistics Probability Experimental Probability

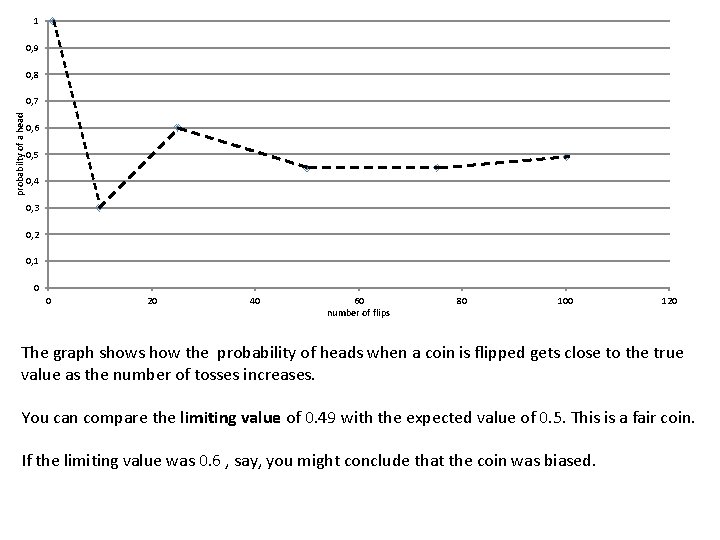
1 0, 9 0, 8 probabilty of a head 0, 7 0, 6 0, 5 0, 4 0, 3 0, 2 0, 1 0 0 20 40 60 number of flips 80 100 120 The graph shows how the probability of heads when a coin is flipped gets close to the true value as the number of tosses increases. You can compare the limiting value of 0. 49 with the expected value of 0. 5. This is a fair coin. If the limiting value was 0. 6 , say, you might conclude that the coin was biased.

Using probability to assess risk The insurance industry uses estimates of probabilities based on limited frequency to assess risk. The probability of you having an accident would be found by looking at the number of people like you who have had accidents compared to the total number at risk. The cost of insurance is based on this probability. Cost of insurance = amount being insured x probability of an accident The actual cost would be greater than this because of the profit the company hopes to make and the cost of their overheads such as salaries etc.

Simulation This is the imitation of a situation (flight simulators? ) of a situation by doing a theoretical study. For example, it is known that a certain commuter train arrives late 30% of the time, early 10% of the time and on time 60% of the time. You could simulate the next ten arrivals by using random digits. You let the digits 0, 1, 2 mean a train is late, the digit 3 mean it is early and the digits 4, 5, 6, 7, 8 and 9 that it is on time. The digits 0 9 4 4 3 5 7 8 1 6 Would then give the first train late, the next three on time the next one early etc.

Your turn