GCSE Solving Quadratic Equations by Factorisation www drfrostmaths

GCSE: Solving Quadratic Equations by Factorisation www. drfrostmaths. com Dr J Frost (jamie@drfrostmaths. com) @Dr. Frost. Maths Last modified: 13 th January 2020

www. drfrostmaths. com Everything is completely free. Why not register? Register now to interactively practise questions on this topic, including past paper questions and extension questions (including UKMT). Teachers: you can create student accounts (or students can register themselves), to set work, monitor progress and even create worksheets. With questions by: Dashboard with points, trophies, notifications and student progress. Teaching videos with topic tests to check understanding. Questions organised by topic, difficulty and past paper.

Recap of Factorisation Factorise the following (intentionally similar looking!) expressions: ? ? ? Recall that we find two numbers which add to give -4 and multiply to give +4.

Test Your Understanding ? 1 ? 2 3 ?

Mini Exercise : : Quadratic Factorisation Recap 1 2 ? ? 3 4 5 ? ? 6 7 ? ? 8 9 10 11 12 N ? ? ?

Solving Quadratic Equations But now we’re moving on. . . Quadratic Expression Equation Click to Move On

Starter = 0 If two things multiply to give 0, what do you know? At least one of those ? things must be 0.

Solving Equations Therefore, how could we make this equation true? ? or ? ?

Quickfire Questions Solving the following. ? ? ?

Exercise 1 Solving the following equations. 1 2 3 4 5 6 7 8 ? ? ? ?

Solving non-factorised equations We’ve seen that solving equations is not too difficult when we have it in the form: [factorised expression] = 0 ? Step 1 ? Step 2 ? Step 3 Step 1: Ensure 0 is on one side of the equation. Step 2: Factorise. Step 3: Consider each factorised term being 0 (as before)

Further example Solve the following. Method 1 Method 2 ? ?

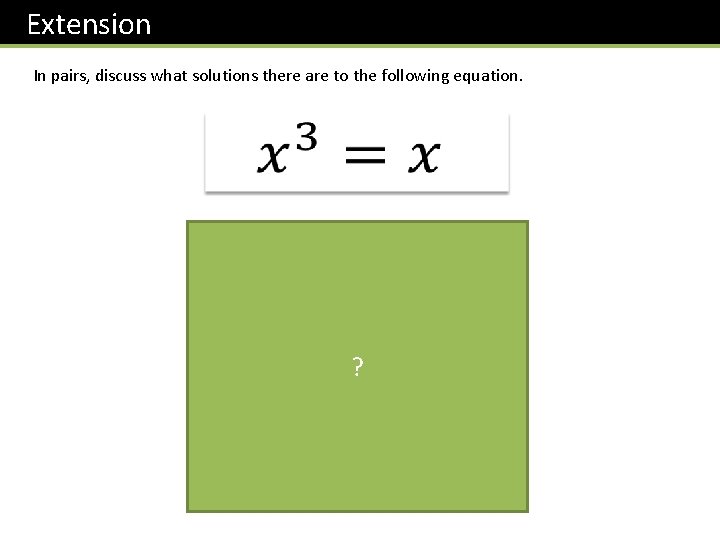
Extension In pairs, discuss what solutions there are to the following equation. ?

Test Your Understanding 1 ? 2 ? 3 ?

Exercise 2 Solve the following equations. 1 2 3 4 5 6 7 8 9 10 11 12 13 x 2 + 7 x + 12 = 0 x 2 + x – 6 = 0 x 2 + 10 x + 21 = 0 x 2 + 2 x + 1 = 0 x 2 – 3 x = 0 x 2 + 7 x = 0 2 x 2 – 2 x = 0 x 2 – 49 = 0 4 x = x 2 10 x 2 – x – 3 = 0 12 y 2 – 16 y + 5 = 0 64 – z 2 = 0 2 x 2 = 8 ? x = -3 or? x = 2 x = -7 or? x = -3 x = -1 ? x = 0 or ? x=3 x = 0 or ? x = -7 x = 0 or ? x=1 x = -7 or? x = 7 x = 0 or ? x=4 x = -1/2 ? or x = 3/5 y = 1/2 or ? y = 5/6 z = 8 ? x = 2 ? x = -3 or x = -4 14 15 16 17 18 19 20 21 N N N 16 x 2 – 1 = 0 x 2 + 5 x = 14 2 x 2 + 7 x = 15 2 x 2 = 8 x + 10 4 x 2 + 7 = 29 x y 2 + 56 = 15 y 63 – 2 y = y 2 8 = 3 x 2 + 10 x x 6 = 9 x 3 – 8 x 4 = 5 x 2 – 4 x 3 = x 2 + x – 1 x 3 + 1 = – x 2 x 4 + 2 x 3 = 8 x + 16 ? x = -7 or? x = 2 x = -5 or? x = 3/2 x = -1 or? x = 5 x = 1/4 ? or x = 7 y = 7 or? y=8 x = -9 or? x = 7 x = -4 or? x = 2/3 x = 1 or? x=2 ? 2 x = 1 or x = 1 ? x = -1 ? x = 2 ? x = 1/4

Harder Equations This is still a quadratic equation! What should we do here? ? Expand everything out first, and simplify. ? ? As before, factorise.

Further Examples ?

Further Examples ? Whenever you have fractions in an equation, your instinct should be to multiply everything through by the denominator of that fraction.

Test Your Understanding 1 ? 2 ?

Exercise 3 Solve the following equations. 1 2 3 4 5 6 7 8 9 10 11 12 N 1 ? ? ? N 2 ? ?

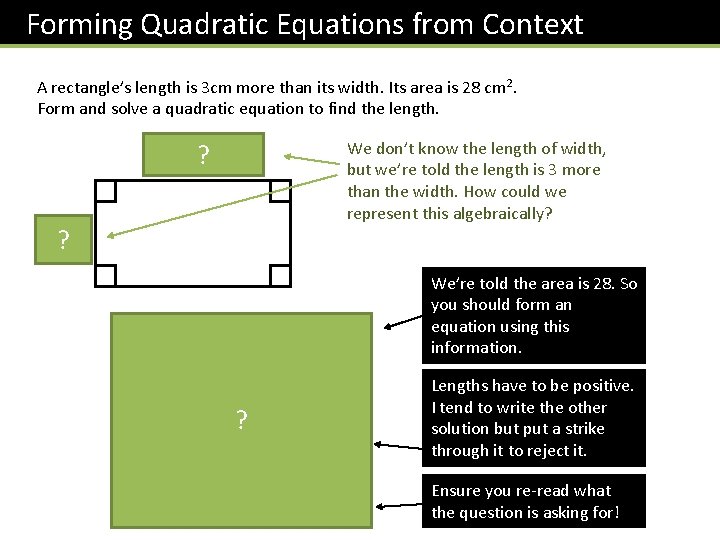
Forming Quadratic Equations from Context A rectangle’s length is 3 cm more than its width. Its area is 28 cm 2. Form and solve a quadratic equation to find the length. We don’t know the length of width, but we’re told the length is 3 more than the width. How could we represent this algebraically? ? ? We’re told the area is 28. So you should form an equation using this information. ? Lengths have to be positive. I tend to write the other solution but put a strike through it to reject it. Ensure you re-read what the question is asking for!

Harder Example Edexcel ? ?

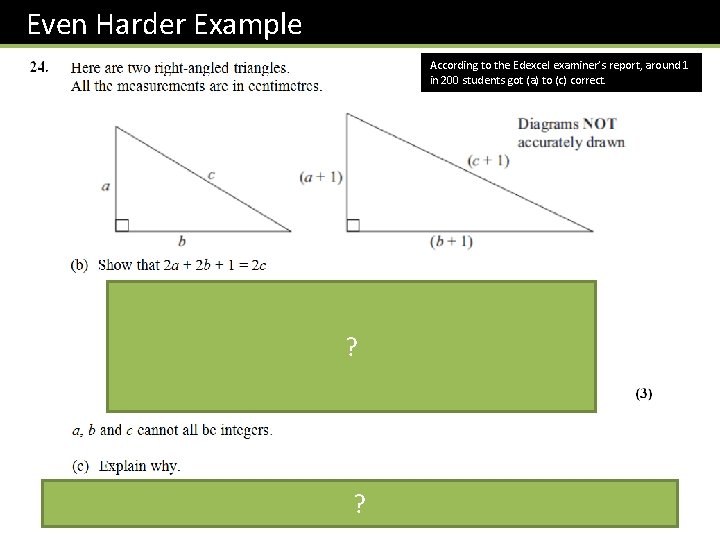
Even Harder Example According to the Edexcel examiner’s report, around 1 in 200 students got (a) to (c) correct. ? ?

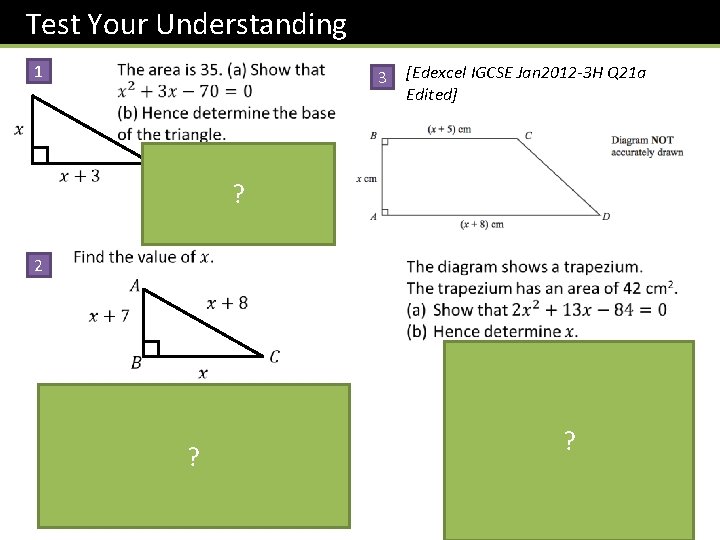
Test Your Understanding 1 3 [Edexcel IGCSE Jan 2012 -3 H Q 21 a Edited] ? 2 ? ?

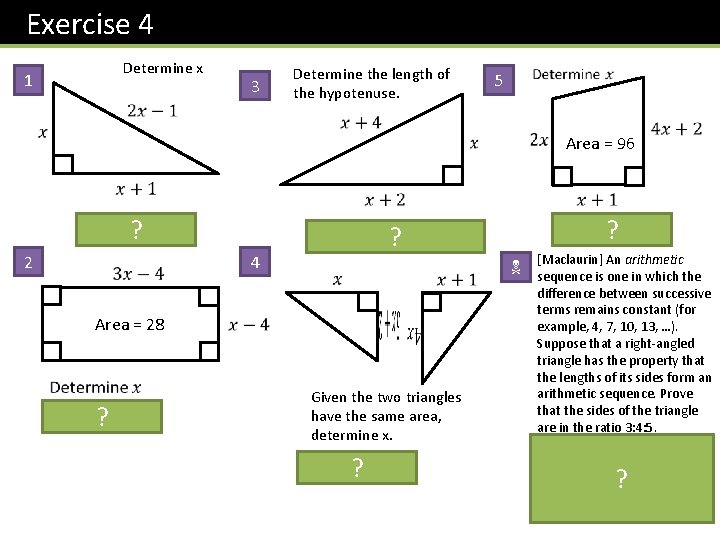
Exercise 4 Determine x 1 3 Determine the length of the hypotenuse. 5 Area = 96 Answer: ? x=3 2 ? ? 4 N Area = 28 ? Answer: x = 5 Given the two triangles have the same area, determine x. ? Answer: x = 2 [Maclaurin] An arithmetic sequence is one in which the difference between successive terms remains constant (for example, 4, 7, 10, 13, …). Suppose that a right-angled triangle has the property that the lengths of its sides form an arithmetic sequence. Prove that the sides of the triangle are in the ratio 3: 4: 5. Solution: Making sides x – a, x and x + a, we obtain x = 4 a by Pythagoras. Thus sides are 3 a, 4 a, 5 a which are in desired ratio. ?

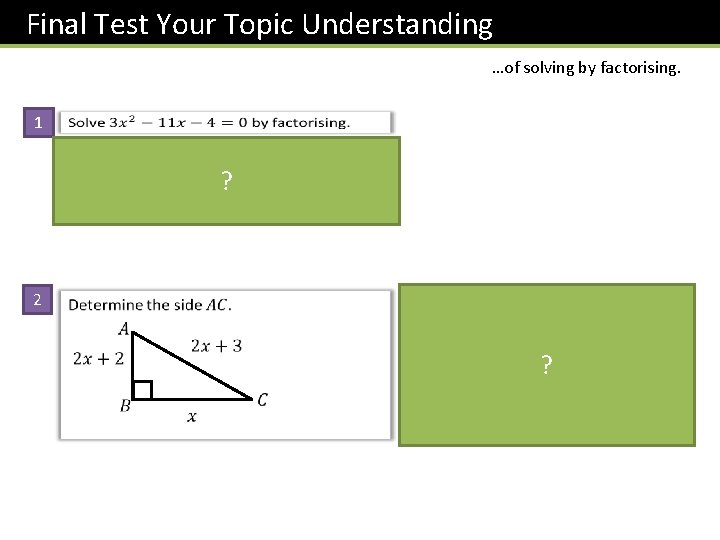
Final Test Your Topic Understanding …of solving by factorising. 1 ? 2 ?