GCSE Maths Algebra and Indices Starter problem solving

GCSE Maths Algebra and Indices
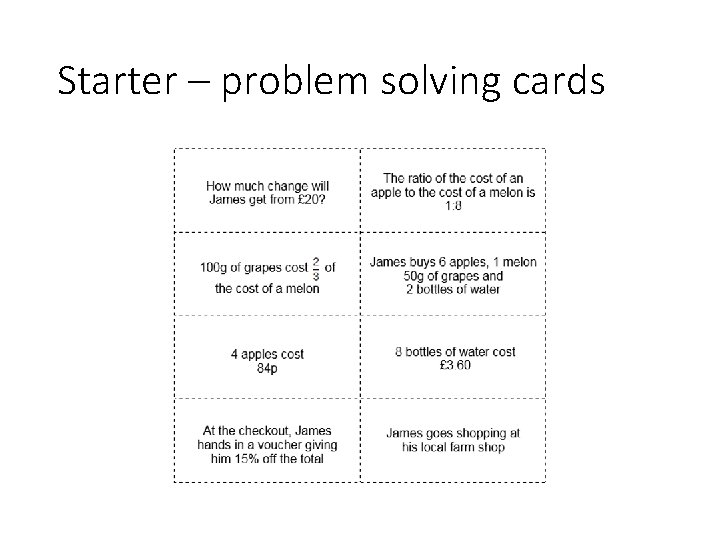
Starter – problem solving cards
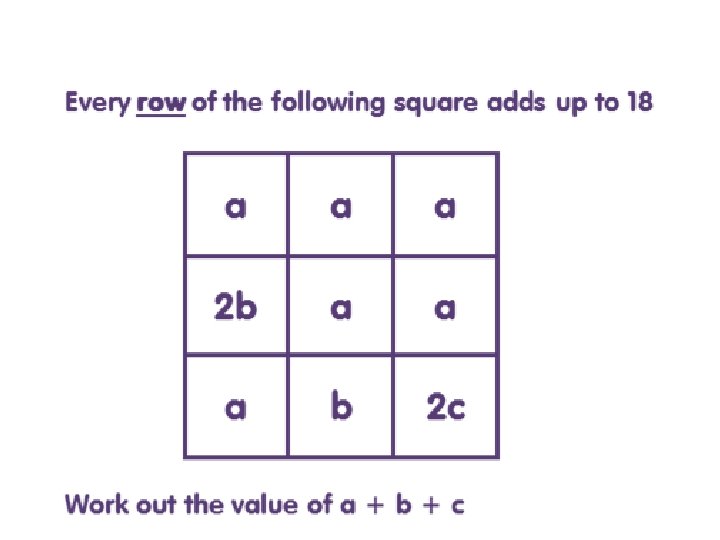
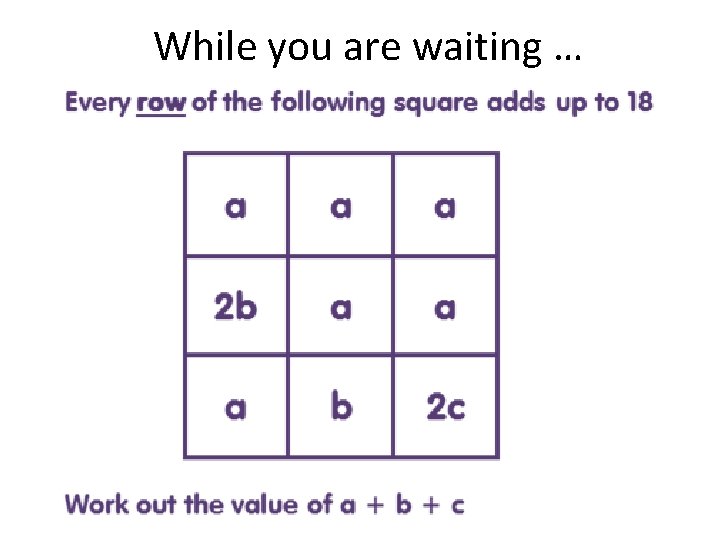
While you are waiting …
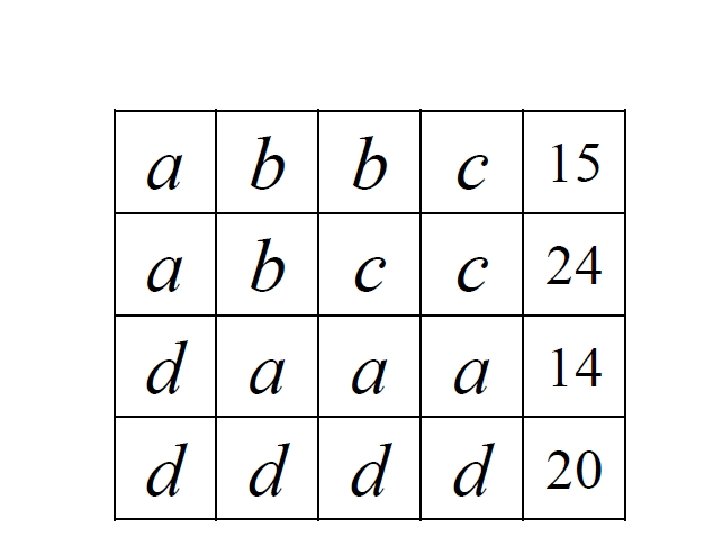

TRUE or FALSE • If the answer is true – hold up your T card • If the answer is false – hold up your F card
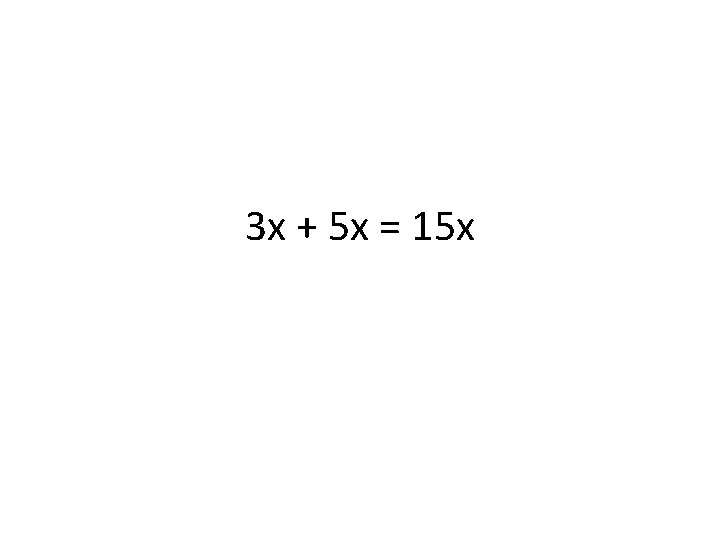
3 x + 5 x = 15 x
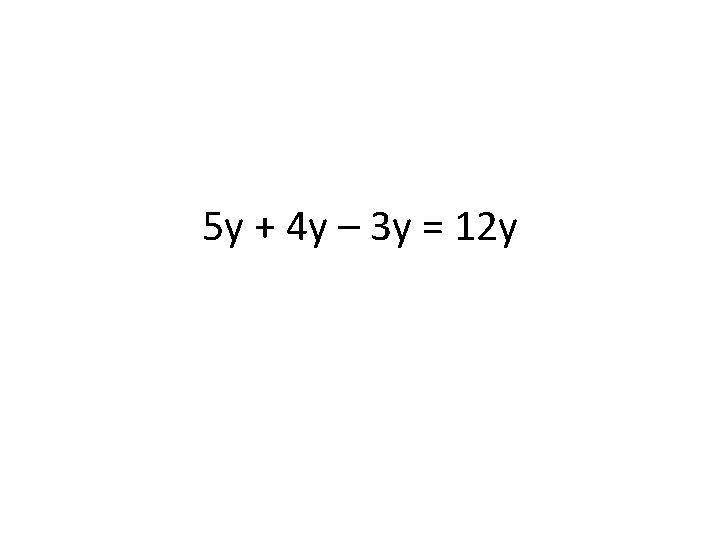
5 y + 4 y – 3 y = 12 y

3 x + 5 y – 2 x + y = 5 x + 6 y
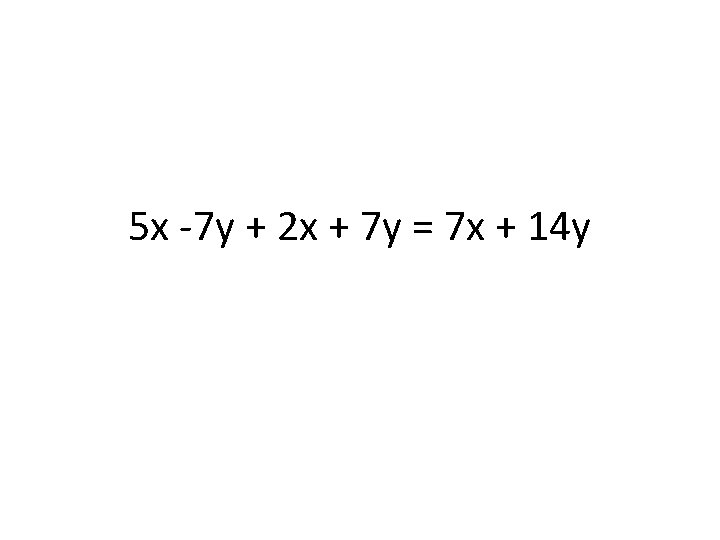
5 x -7 y + 2 x + 7 y = 7 x + 14 y
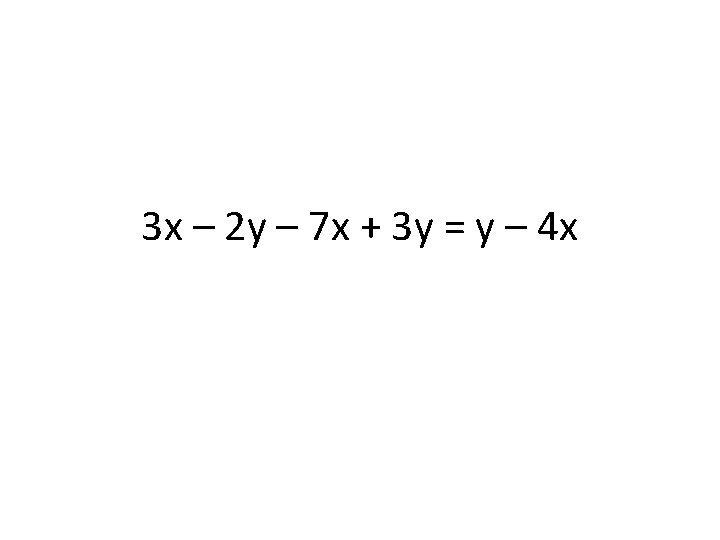
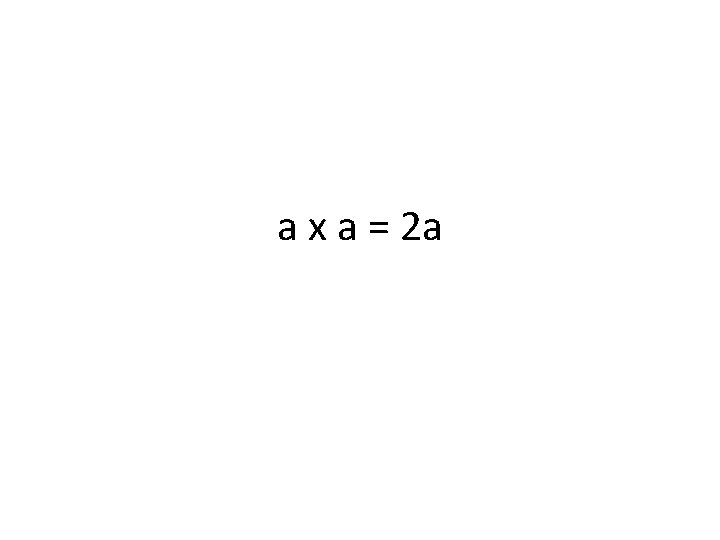
a x a = 2 a
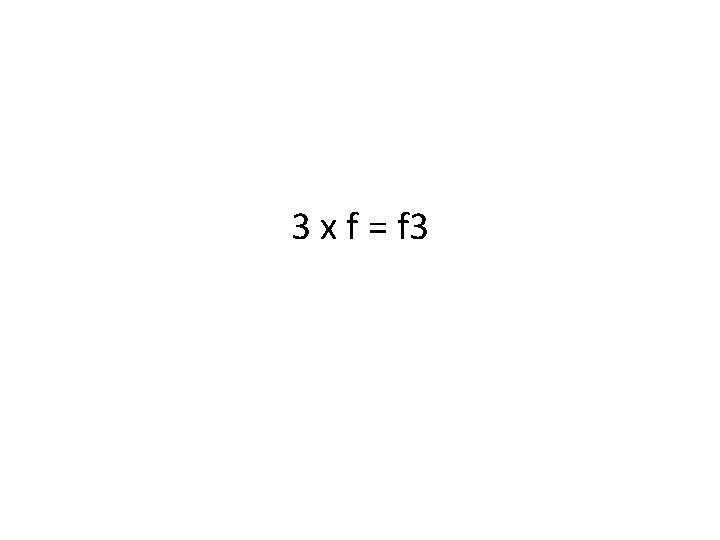
3 x f = f 3

3 x a x b = 3 ab end of true and false
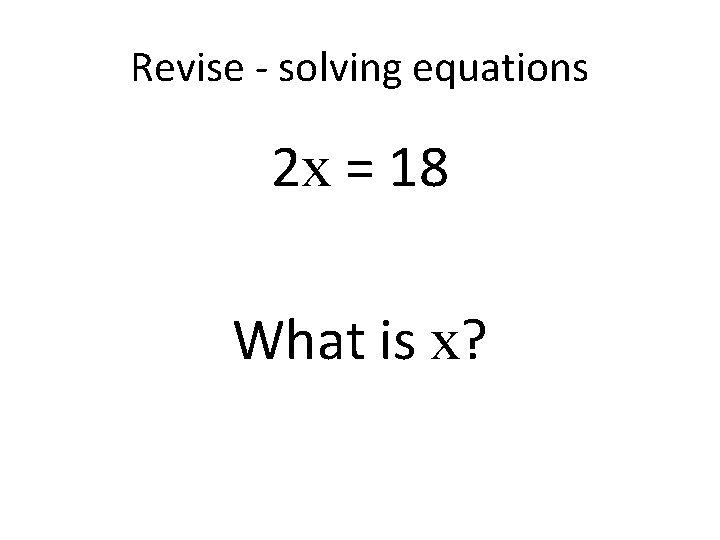
Revise - solving equations 2 x = 18 What is x?
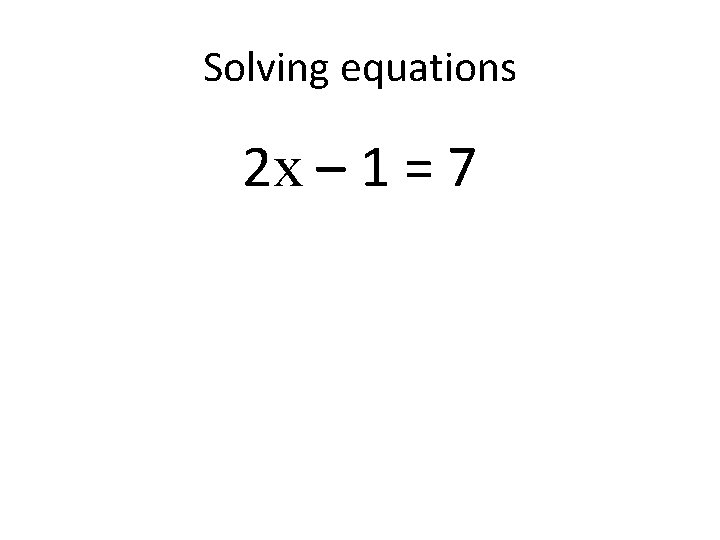
Solving equations 2 x – 1 = 7

Solving equations 3 x + 2 = 23

Solving equations t + t = 4. 5
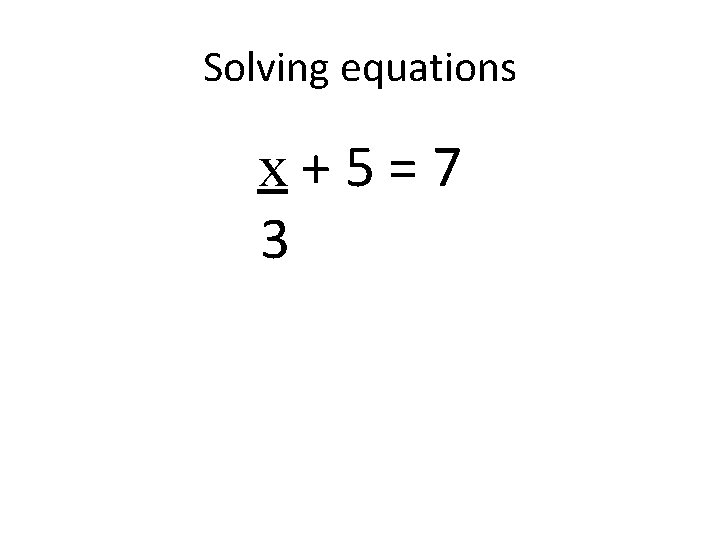
Solving equations x+5=7 3
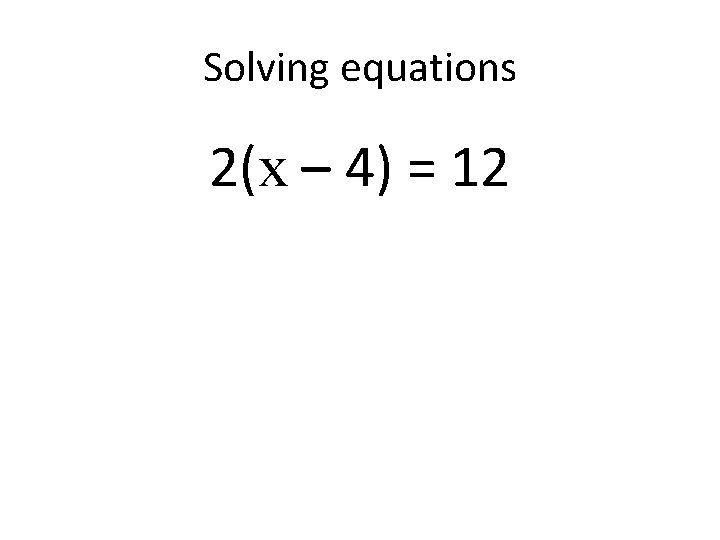
Solving equations 2(x – 4) = 12
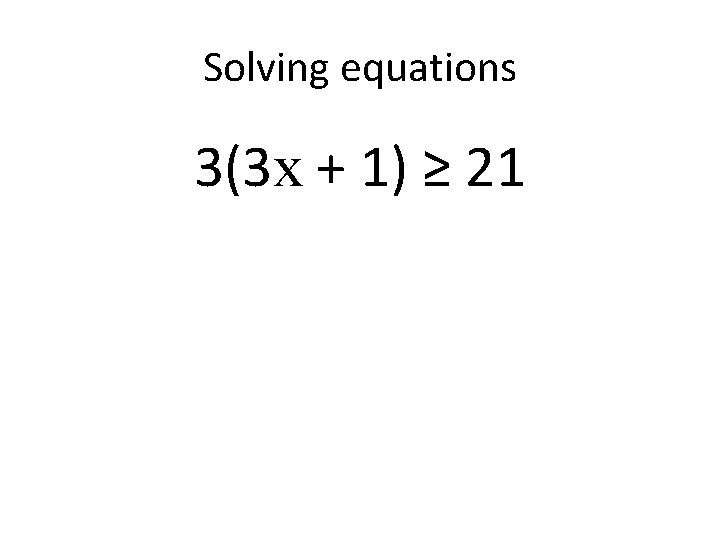
Solving equations 3(3 x + 1) ≥ 21
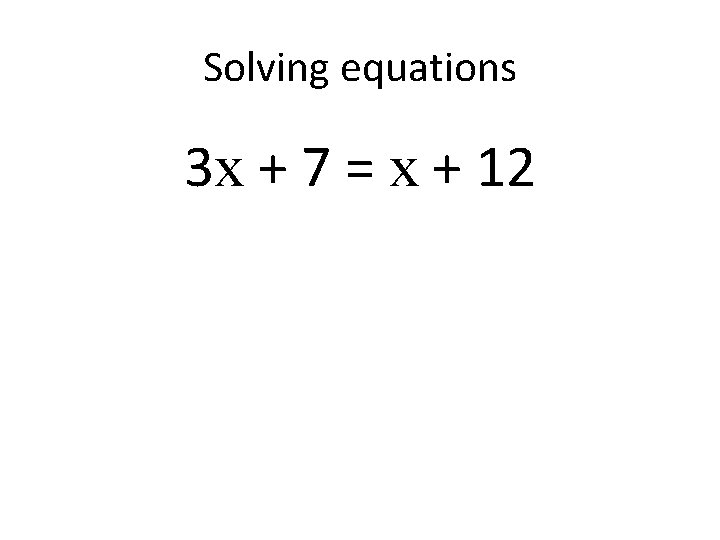
Solving equations 3 x + 7 = x + 12
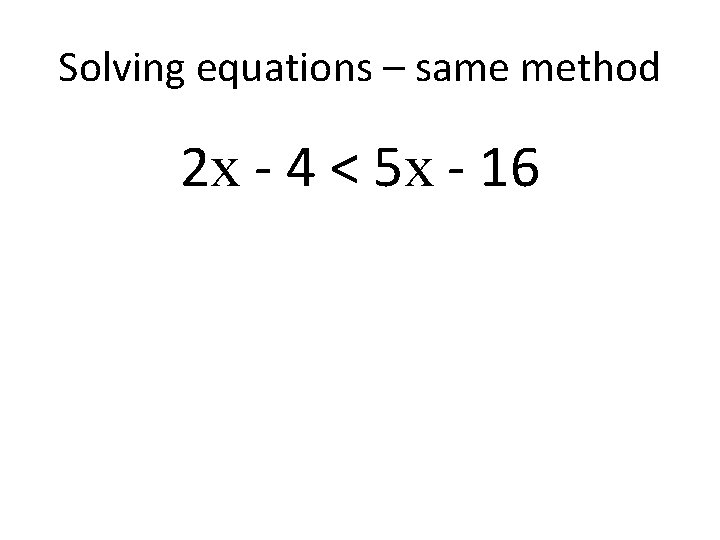
Solving equations – same method 2 x - 4 < 5 x - 16

3 x x == 12 4 1 2 xx- =7 =41 2 3 xx+ = 5 =623 7 x x == 63 9 4 = -5 xx +=7 -12 5 xx== 12 48 7 2 xx- = 11= 85 8 xx – 8==-5 -13 xx+=8 -10 = -2 3 6 4 9

Rearranging a formula • How would you find x when 5 x + 3 = 23? • How would you find x when 5 x + y = z?



Rearranging a formula v = u + at • Make u the subject of the formula • Make a the subject of the formula • Make t the subject of the formula • me

Rearranging a formula v = 6 u + 5 t Make u the subject of the formula Make t the subject of the formula you

Using algebra to solve problems … (this one together) Mary and John have £ 50 altogether. Mary has £ 12 more than John. Write an equation for the money they have altogether and using the equation, work out how much money they have each.

(this one together) The perimeter of a rectangle is 56 cm. One side is 4 cm longer than the other. Write an equation to show this information and find the length of the sides.

Exam question – “Total” • • Three numbers have a total of 30 Two of the numbers are equal. The third is half the size of the other two. Find the numbers.

Exam question – “Whole Numbers” • • Three whole numbers have a total of 100 Two of the numbers have a difference of 7 Two of the numbers are the same Find the numbers

More practice for changing the subject Worksheet from Mathswatch

Identity Equation Expression Formula Recognise Words Used In Algebra

6 x + 12 A : Identity v B : Equation v C : Expression v D : Formula v

6 x + 12 A : Identity v B : Equation v C : Expression v D : Formula v

4 x + 2 = 18 A : Identity v B : Equation v C : Expression v D : Formula v

4 x + 2 = 18 A : Identity v B : Equation v C : Expression v D : Formula v

6 x + 12 = 3(2 x + 4) A : Identity v B : Equation v C : Expression v D : Formula v

6 x + 12 = 3(2 x + 4) A : Identity v B : Equation v C : Expression v D : Formula v

v = u + at A : Identity v B : Equation v C : Expression v D : Formula v

v = u + at A : Identity v B : Equation v C : Expression v D : Formula v

a² + 2 a = a ( a + 2 ) A : Identity v B : Equation v C : Expression v D : Formula v

a² + 2 a = a ( a + 2 ) A : Identity v B : Equation v C : Expression v D : Formula v

A = π r² A : Identity v B : Equation v C : Expression v D : Formula v

A = π r² A : Identity v B : Equation v C : Expression v D : Formula v

9 b - l 0 A : Identity v B : Equation v C : Expression v D : Formula v

9 b - l 0 A : Identity v B : Equation v C : Expression v D : Formula v

2 x² + 3 x – 7 = 0 A : Identity v B : Equation v C : Expression v D : Formula v

2 x² + 3 x – 7 = 0 A : Identity v B : Equation v C : Expression v D : Formula v

An expression is … A : 8 x + 2 = 12 v B : 8 x + 2 v C : 8 x + 2 = C v D : 8 x + 2 = 2(4 x + 1) v
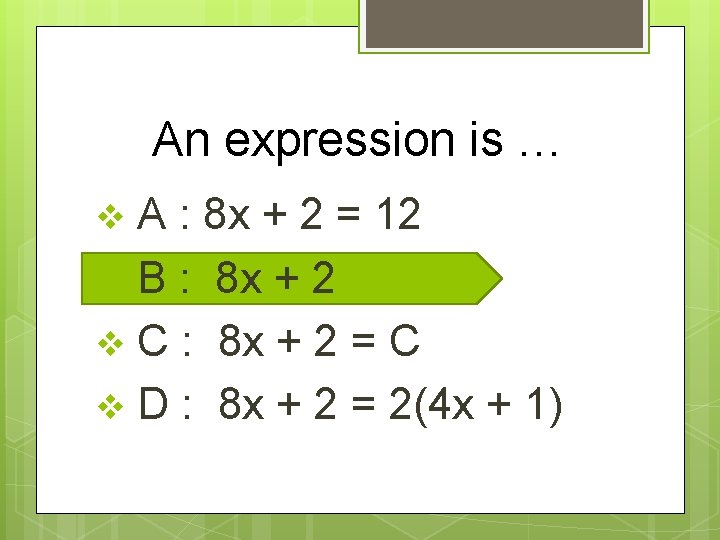
An expression is … A : 8 x + 2 = 12 v B : 8 x + 2 v C : 8 x + 2 = C v D : 8 x + 2 = 2(4 x + 1) v

A formula is … A : 8 x + 2 = 12 v B : 8 x + 2 v C : 8 x + 2 = C v D : 8 x + 2 = 2(4 x + 1) v

A formula is … A : 8 x + 2 = 12 v B : 8 x + 2 v C : 8 x + 2 = C v D : 8 x + 2 = 2(4 x + 1) v

An identity is … A : 8 x + 2 = 12 v B : 8 x + 2 v C : 8 x + 2 = C v D : 8 x + 2 = 2(4 x + 1) v

An identity is … A : 8 x + 2 = 12 v B : 8 x + 2 v C : 8 x + 2 = C v D : 8 x + 2 = 2(4 x + 1) v

An equation is … A : 8 x + 2 = 12 v B : 8 x + 2 v C : 8 x + 2 = C v D : 8 x + 2 = 2(4 x + 1) v

An equation is … A : 8 x + 2 = 12 v B : 8 x + 2 v C : 8 x + 2 = C v D : 8 x + 2 = 2(4 x + 1) v

You know how to expand with a single bracket Expand 2(3 x + 5)

• FSMA Factor cards slides. ppt • FSMA Factor cards set. pdf • FSMA Factor cards student. pdf

Expanding double brackets You can teach this using the FOIL method or the box method or both. For the FOIL method there are loads of videos on You. Tube including songs. The 16 -18 students will have a method from school. The box method is in this document Expanding Double Brackets box method. docx

Expanding double brackets • (x + 6)(x + 3) • (x – 6)(x – 3) • (x + 6)(x – 3)

Factorising quadratic equations Factorise x 2 + 6 x + 8 Factorise x 2 + 6 x - 16 Factorise x 2 - 7 x + 12 Some more examples …… Talk about solving
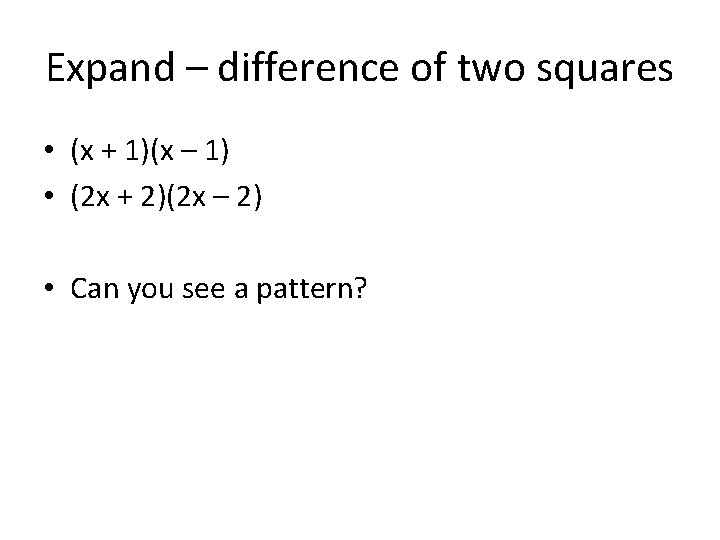
Expand – difference of two squares • (x + 1)(x – 1) • (2 x + 2)(2 x – 2) • Can you see a pattern?
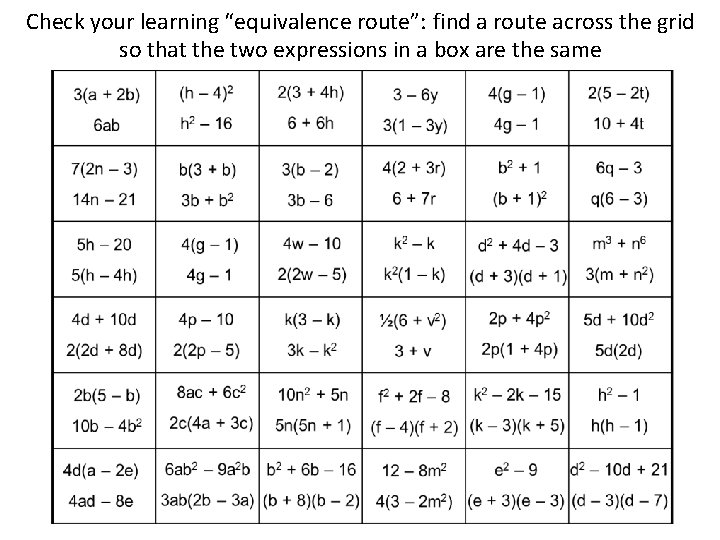
Check your learning “equivalence route”: find a route across the grid so that the two expressions in a box are the same

Just Maths – expand simplify Connect 4

New topic - indices • What does the word “reciprocal” mean?

Let’s start with 10 quick questions

Powers, Roots and Reciprocals Write down the value of 2 5

Powers, Roots and Reciprocals Which is bigger 32 or 23? You must show your working to a quickfire question

Powers, Roots and Reciprocals

Powers, Roots and Reciprocals

Powers, Roots and Reciprocals

Powers, Roots and Reciprocals

Powers, Roots and Reciprocals Write down the value of 3 3

Powers, Roots and Reciprocals Write down the reciprocal of 4.

Powers, Roots and Reciprocals

Powers, Roots and Reciprocals

Powers, Roots and Reciprocals

Well Done!!

Powers and indices Play powers. ppt Learning Objective: Use the “laws of indices” to multiply and divide numbers written in index notation

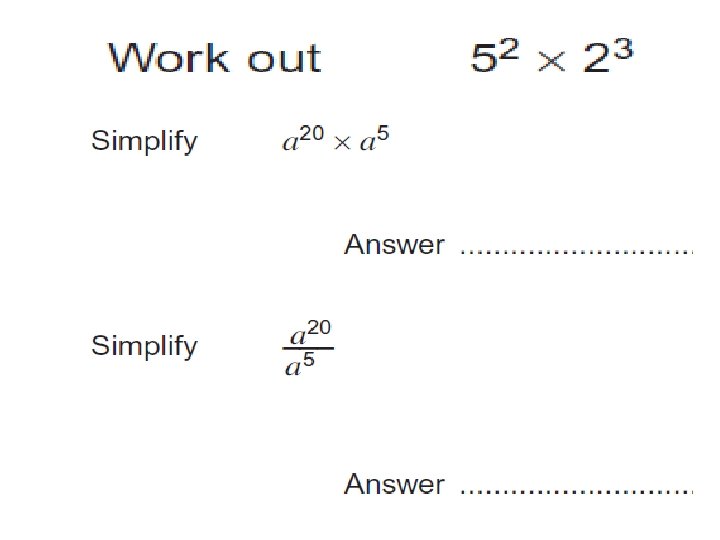
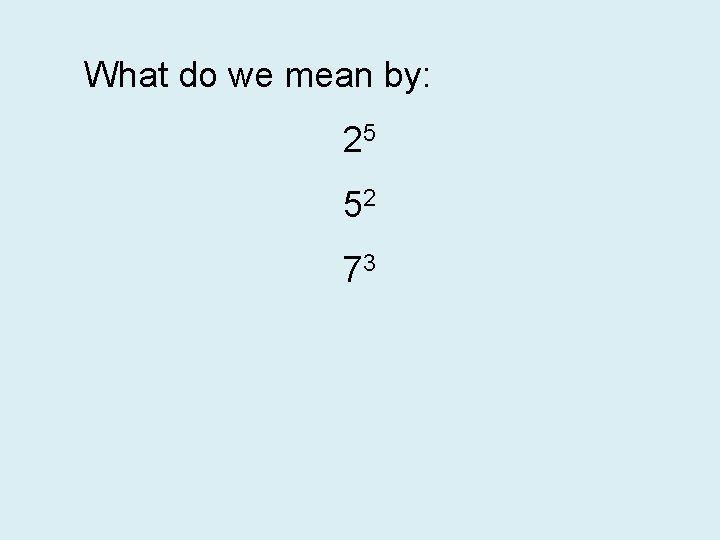
What do we mean by: 25 52 73
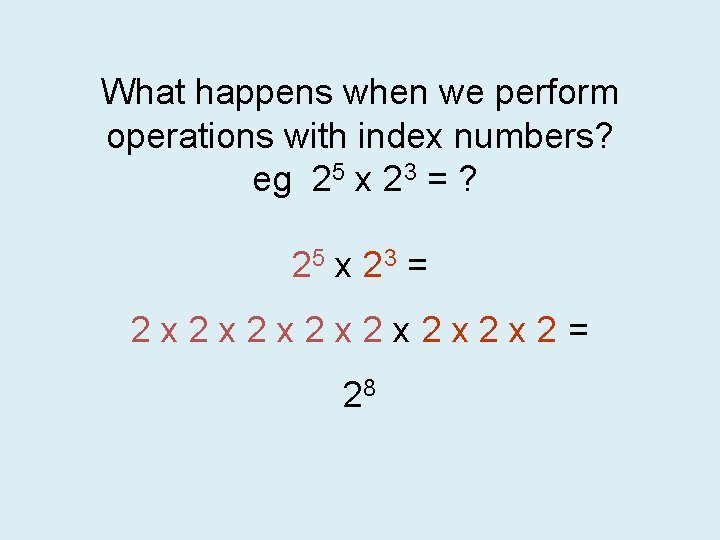
What happens when we perform operations with index numbers? eg 25 x 23 = ? 25 x 23 = 2 x 2 x 2= 28

Try this one 73 x 7 2 x 7 = ? 73 x 72 x 7 = 7 x 7 x 7 x 7= 76
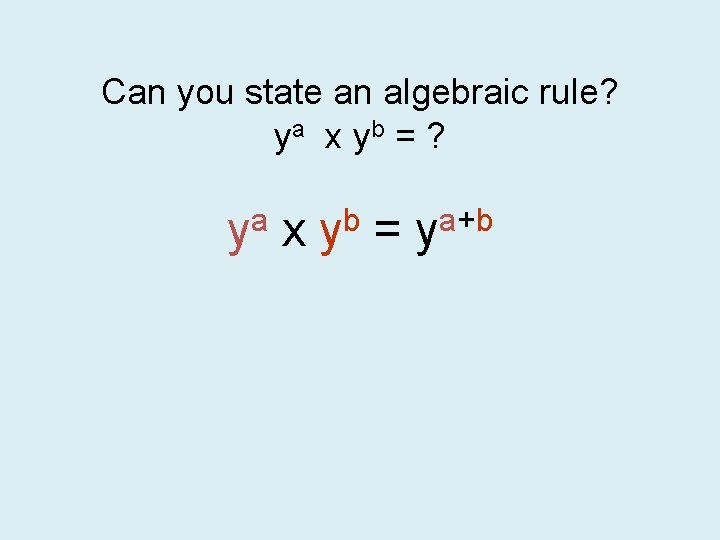
Can you state an algebraic rule? ya x yb = ? a y x b y = a+b y
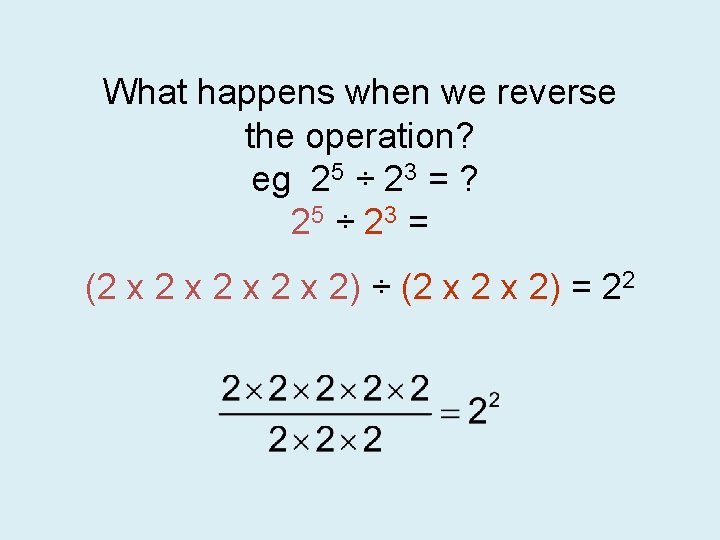
What happens when we reverse the operation? eg 25 ÷ 23 = ? 25 ÷ 23 = (2 x 2 x 2) ÷ (2 x 2) = 22

Try this one 76 ÷ 7 2 = ? 76 ÷ 72 = 7 4
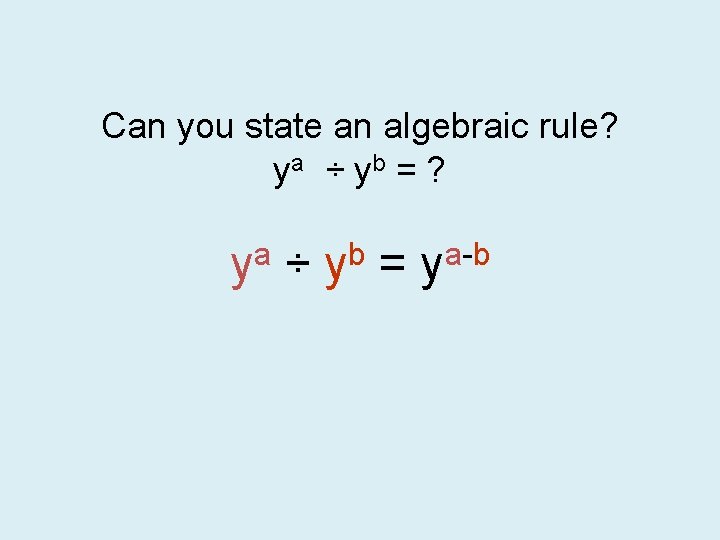
Can you state an algebraic rule? ya ÷ yb = ? ya ÷ yb = ya-b

Extending our understanding. . .

Complete this table 25 24 23 = = = 32 16 8 4

If 20 = 1, what about 30 ? It is also the fact that 30 = 1 In fact, anything to the power of zero is one.
http: //www. transum. org/Maths/Activity/Algebr a/Indices. asp Nice true or false activity – could use a smart board – students could get involved – recommended!

• The next slide is for practice.

- Slides: 97