GCSE Iteration Dr J Frost jfrosttiffin kingston sch

GCSE Iteration Dr J Frost (jfrost@tiffin. kingston. sch. uk) www. drfrostmaths. com @Dr. Frost. Maths Last modified: 2 nd June 2020

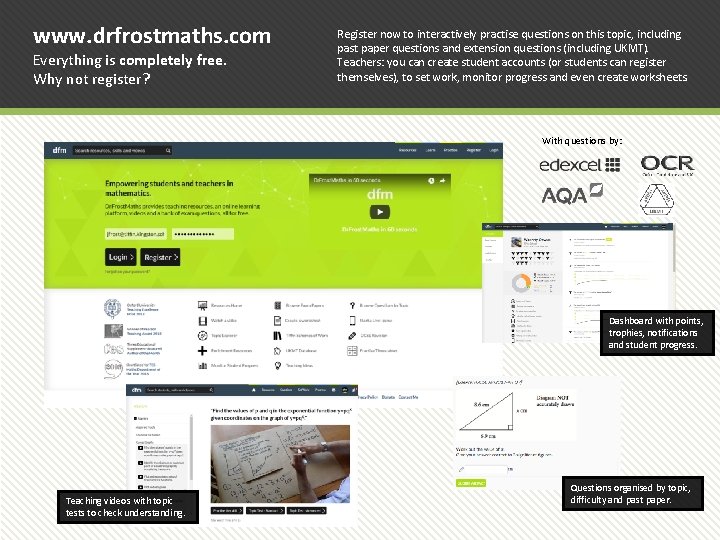
www. drfrostmaths. com Everything is completely free. Why not register? Register now to interactively practise questions on this topic, including past paper questions and extension questions (including UKMT). Teachers: you can create student accounts (or students can register themselves), to set work, monitor progress and even create worksheets. With questions by: Dashboard with points, trophies, notifications and student progress. Teaching videos with topic tests to check understanding. Questions organised by topic, difficulty and past paper.

Term to term formulae ? ? ?

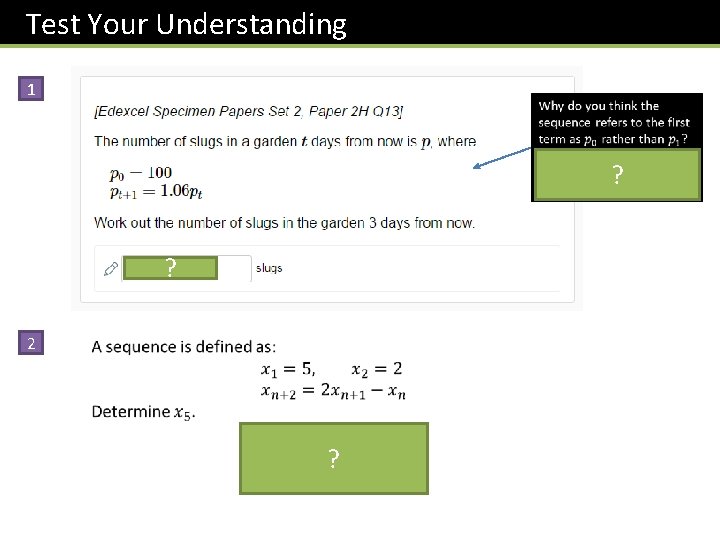
Test Your Understanding 1 ? 119 ? 2 ?

Iteration ? You will always be given a starting value in the exam. The 0 means we’ve done “ 0 iterations”. ? a Use your term-to-term formula to get successively better solutions to the original equation. ? ? We could keep going for ever to keep getting more accurate solutions. The exam will usually tell you how many iterations it wants (here we did 4).

Why use iteration then? In the previous example, we could have found out the ‘exact’ answer using the quadratic formula. However, for some functions, the exact solution is either complicated and difficult to calculate: ? or there’s no ‘exact’ expression at all! (involving roots, sin, cos, etc. ) ? Exact solution not expressible Iteration therefore is an intelligent way of doing ‘trial and improvement’ that gets us the solution correct to progressively more and more decimal places on each iteration, even if there is no way to write the answer in a 100% accurate way.

Another Example [Edexcel New SAMs Paper 3 H Q 14 c] Bro Tip: Use the target expression as clues for how to rearrange. Each term is over 4, which suggests we need to divide by 4 at some point. ? ? For iterative methods, give your answer as a decimal NOT as a fraction. Why? Because fractions imply an exact answer, but this method only gets an approximation of the solution) ?

Test Your Understanding ? ?

Roots and Showing Roots Lie in a Range a ? b ? c We could have chosen any starting value between 0 and 1. Preferably near the middle! ?

Exercise 1 3 ? ? ? ? ? 4 ? ? 2 ? ?

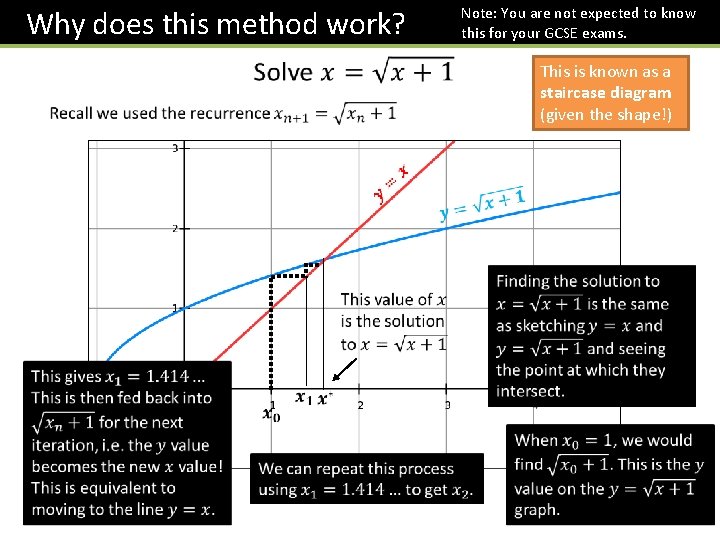
Why does this method work? Note: You are not expected to know this for your GCSE exams. This is known as a staircase diagram (given the shape!)

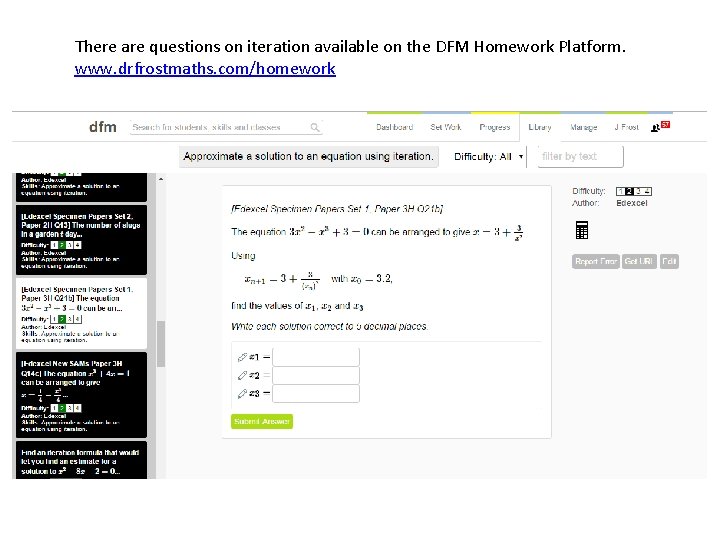
There are questions on iteration available on the DFM Homework Platform. www. drfrostmaths. com/homework