Gazdasgtudomnyi Kar Gazdasgelmleti s Mdszertani Intzet Optimalizcis eljrsok

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Optimalizációs eljárások közgazdasági alkalmazása (neptunkód: GTGKG 4851) Ph. D képzés tárgyjegyző: Dr. Karajz Sándor

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Tantárgy feladata és célja A hagyományos és a modern – alapvetően a biológiai evolúció analógiájára épülő - optipalizációs eljárások megismerése illetve összehasonlítása. Az utóbbi évtizedekből számos példát találunk a szakirodalomban az említett modern eljárások alkalmazására. A tárgy további célja, hogy a hallgatók az említett alkalmazási lehetőségeket - különös tekintettel a közgazdasági illetve gazdasági felhasználásra – megismerjék, értékeljék, valamint lehetőség esetén saját kutatómunkájukban alkalmazzák.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet A tantárgy tartalma Ø Optimalizációs alapfogalmak, Hagyományos optimalizációs eljárások • • Gradiens alapú módszerek, Kimerítő keresésen alapuló eljárások Ø Véletlent használó optimalizációs eljárások • • • Tabukeresés Szimulált lehűtés Evolúciós algoritmusok Ø A biológiai evolúció mintájára működő eljárások • • • Replikátordinamika Szinergetika Evolúciós játékelmélet Genetikus algoritmusok Evolúciós stratégiák Ø A biológiai evolúció mintájára működő optimalizációs eljárások gyakorlati alkalmazásai (gyártási folyamatok tervezése, hálózat optimalizáció, irányítástechnikai alkalmazás, képfeldolgozás) Ø Közgazdasági alkalmazások (Cobweb-típusú piac modellezése, tanulási folyamatok leírása, technológiai változások modellezése, értékpapír-piaci mechanizmusok, valutaárfolyamok alakulása)

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Tanulmányok és előadásanyagok http: //gtk. unimiskolc. hu/gei/letoltesek? %20 file_category_id= 895&order_type=NAME&view_type=LIST

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Tanulmány választás https: //docs. google. com/spreadsheets/d/1 GCc. Z T 0 HXWNaar. MFc. PS_VC 2 nw. OSW_VFi. Uc. Z 7 Wb. DLZ u 5 U/edit? usp=sharing

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Kezdjük az utazó ügynök problémával • példa a bonyolultság-elmélet által NP-nehéznek nevezett problémára • A probléma: Adva van n város, illetve az útiköltség bármely két város között, keressük a legolcsóbb utat egy adott városból indulva, amely minden várost pontosan egyszer érint, majd a kiindulási városba ér vissza.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Az utazó ügynök probléma bonyolultsága 1. • [(n-1)!]/2 út közül tudunk választani, ahol n a várások száma • a legkézenfekvőbb megoldás az összes permutáció végignézése, de tekintve, hogy ez n! darab permutációt jelent (ahol n a városok száma), nagyobb n-ekre ez a megoldás kivitelezhetetlen. • Pl: 50! = 3*1064

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Az utazó ügynök probléma bonyolultsága 2. Már 20 város esetén sem célravezető az összes permutáció végignézése. Ha lenne egy számítógépünk, ami másodpercentként 1 milliárd műveletet lenne képes megoldani, akkor a 20!-t közel 28159 nap alatt tudná kiszámolni, ami több mint 77 év.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Alkalmazási területek • Járatoptimalizálás • Vállalaton belüli anyagmozgatás • Nyomtatott áramkör tervezés (minimális vezetékfelhasználás) • Genetika (DNS részletek összeillesztése) • Folyamatlépések sorrendjének meghatározása (minimalizálás)

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet 1. téma Optimalizálási alapfogalmak, optimalizálási eljárások csoportosítása és jellemzése

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Tartalom 1. 2. 3. 4. Optimalizálási alapfogalmak Optimalizációs eljárások csoportosítása Gradiens alapú módszerek Kimerítő keresésen alapuló eljárások

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet 1. Optimalizálási alapfogalmak

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Optimalizálás Ø Általános értelmezésben: Legjobb állapot illetve cselekvés kiválasztására alkalmas eljárás, valamely előre meghatározott kritérium alapján. Ø Közgazdasági értelemben: Az optimalizálás jelentése a gazdasági erőforrásokkal való ésszerű gazdálkodás, amely a ráfordításokat és a kibocsájtásokat méri össze, illetve a kibocsájtás adott nagyságának elérése minél kisebb mértékű ráfordítások felhasználásával.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Optimalizálási probléma ØAdott egy szabad paraméterekkel rendelkező rendszer (független változók) ØAdott egy objektív mérce, a modell minőségi jellemzője ØFeladatunk a paraméterek olyan beállításának megtalálása, amely minimalizálja vagy maximalizálja ezt a minőségi jellemzőt.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Objektív mérce ØAz objektív mércét a felhasználó preferenciája adja meg. ØLehet „jóság” vagy költség: maximum vagy minimum ØEgész rendszerre vonatkozó szélsőérték: globális minimum vagy maximum

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Szélsőérték ØEgész rendszerre vonatkozó szélsőérték: globális minimum vagy maximum. ØLokális szélsőérték: nem a teljes értelmezési tartományt, hanem csak egy pont bizonyos környezetét vizsgáljuk. ØGlobális szélsőérték lokális szélsőérték is.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Korlátos keresési tér Gyakran előfordul a valós helyzetekben, hogy egyes erőforrásokból, kapacitásokból csak korlátos mennyiség áll rendelkezésre, melyek megkötéseket jelentenek az érvényes keresési térre vonatkozóan.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet 2. Optimalizálási eljárások csoportosítása

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Csoportosítás 1. Ø Feltételek szerint • feltétel nélküli szélsőérték-feladatok • feltételes szélsőérték-feladatok Ø Változók száma szerint • egyváltozós • többváltozós Ø Célfüggvény típusa szerint • nemlineáris célfüggvény • lineáris célfüggvény

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Csoportosítás 2. Ø optimalizációs algoritmusok (lineáris + nem lineáris programozás) Ø iteratív módszerek (gradiens alapú módszerek Ø heurisztikák (véletlent használó módszerek)

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Optimalizációs eljárások • George Dantzig szimplex algoritmusa a lineáris programozás számára • A szimplex algoritmus kiterjesztései a kvadratikus programozás és a törtlineáris programozás számára • A szimplex algoritmus módosításai a hálózati optimalizálásra • Kombinatorikus algoritmusok

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Iteratív módszerek Ø Ø Ø Newton-módszer Gradienseken és közelítésükön, vagy szubgradiensen alapuló módszerek: Kvázi-Newton-módszerek: iteratív módszerek közepes dimenziószámra. Konjugált gradiens módszerek Belsőpontos módszerek Gradiens módszer Szubgradiens módszerek Köteg leszállási módszer Ellipszoid-módszer Redukált gradiens módszer Szimultán perturbációs sztochasztikus approximáció

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Heurisztikák • • • Memetikus algoritmus Differenciális evolúció Differenciális keresőalgoritmus Dinamikus relaxáció Genetikus algoritmusok Hegymászó heurisztika Részecskeraj optimalizáció Mesterséges méhkolónia optimalizáció Szimulált edzés Tabu keresés

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Csoportosítás 3. Az optimalizálási módszereket lehet az alapján is csoportosítanunk, hogy a számítógép milyen szerepet tölt be az optimalizálás során. Két fő csoportot különböztethetünk meg: Ø analitikus optimalizálás, Ø szimulációs optimalizálás.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Csoportosítás 3. Az analitikus optimalizálás alatt azt értjük, amikor a célfüggvény és a korlátozó feltételek matematikailag jól analizálható formában írhatók le, általában képezhető a célfüggvény deriváltja (többváltozós esetben a gradiens vektor) és második deriváltja (Hesse-mátrix), s számítógépes eszközök alkalmazása nélkül kezelhető a feladat. Természetesen a számítások elvégzéséhez ekkor is számítógépet veszünk igénybe, sőt, a széles körű gyakorlati alkalmazhatóságot a számítógépek elterjedése tette lehetővé, ami lényeges szemléleti változással is járt. A szimulációs optimalizálás olyan optimalizálási feladat, ahol a célfüggvény és/vagy a kényszerfeltételek csak számítógépes szimulációval értékelhetők ki. Azaz, a célfüggvény és/vagy a kényszerfeltételek nem fejezhetők ki analitikus formában és/vagy a rendszerváltozók sztochasztikus függvényeiként adhatók meg.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Csoportosítás 4.

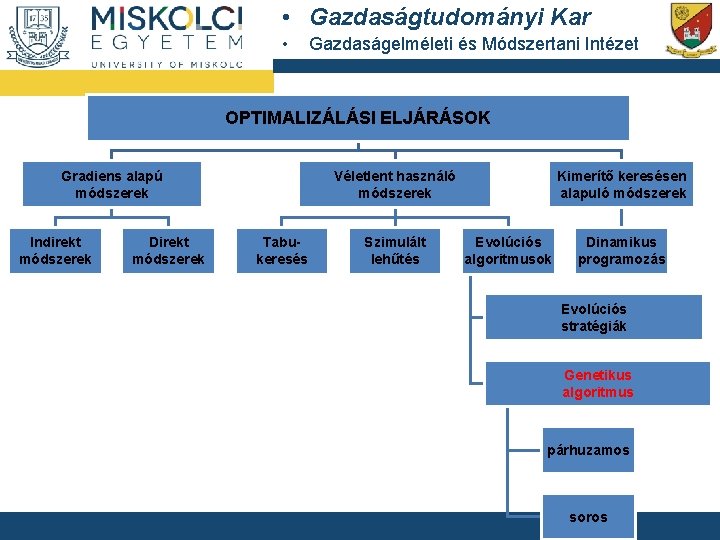
• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet OPTIMALIZÁLÁSI ELJÁRÁSOK Gradiens alapú módszerek Indirekt módszerek Direkt módszerek Véletlent használó módszerek Tabukeresés Szimulált lehűtés Kimerítő keresésen alapuló módszerek Evolúciós algoritmusok Dinamikus programozás Evolúciós stratégiák Genetikus algoritmus párhuzamos soros

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet 3. Gradiens alapú módszerek

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet A gradiens alapú módszereket már a 17. századtól kezdve tanulmányozták. Lényegük, a függvény értékének megváltozásán alapul, tehát feltételezik a derivált függvény létezését vagy legalább az értékének numerikus megközelítését. A valós életben ez ritkán teljesül, ezért csak szűk tartományban alkalmazható ez a módszer, nem tekinthető kellően robusztusnak.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Fajtái – direkt – indirekt Jellemzők – Lokális vizsgálódás – Feltételezik a deriváltfüggvény létezését

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Indirekt módszerek ØIndirekt módszerek esetén nem a függvény értékeit vizsgáljuk csak a derivált vagy gradiens függvény zérus helyeit keressük. Így olyan helyeket találunk meg, melyhez illesztett érintősík meredeksége minden irányban nulla. Így az összes lokális szélsőértéket megtaláljuk ØA lokális szélsőértéket a gradiensfüggvény nullává tételével keresik meg. ØA differenciáláson alapuló egydimenziós szélsőértékkeresés többdimenziós általánosítása

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Direkt módszerek ØA direkt módszerek esetén a függvény felületének egy pontjáról indulunk el és a lokális gradiens irányába haladunk, mert ez mutatja meg a legmeredekebb utat a célunk felé, hegymászásnak is nevezik ezeket az eljárásokat. ØA lokális minimumot a lokális gradiens irányába való elmozdulással igyekeznek elérni a felületen. ØHegymászás (hill-climbing) fogalma: a lokális szélsőérték eléréséhez a „legmeredekebb emelkedőn kell felmászni”, vagy „a legmeredekebb lejtőn kell leereszkedni”.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Robusztusság 1. Mindkét módszer csak lokálisan vizsgálódik, az aktuális (kiindulási) pont környezetében keresi a legjobb szélsőértéket. Egy kisebb abszolút értékű szélsőérték közeléből indítva az eljárást gyakran nem találja meg a nagyobb abszolút értékű szélsőértéket. Sőt, ha már megtalálta az eljárás a kisebb abszolút értékű szélsőértéket, akkor véletlenszerű újraindítással vagy más „trükkel” lehet csak „rávenni” a nagyobb abszolút értékű szélsőérték keresésére.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Robosztusság 2. A gradiens alapú módszerek feltételezik a deriváltfüggvény létezését. Számos gyakorlati problématér nem biztosít elegendő simaságot az optimalizálandó függvénynek, ebből következően nem létezik deriváltfüggvény sem. A valós életben nem mindenütt folytonos, sok lokális szélsőértékkel rendelkező függvényekkel és zajos keresési terekkel kell dolgozni.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet 4. Kimerítő keresésen alapuló módszerek

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Egy véges vagy diszkretizált végtelen problématérben az algoritmus egyesével végig nézi a tér összes pontját. A problématér pontjait legtöbbször leírhatjuk egy fával. Ezután teljes bejárást végezve, egyszerű módszerrel megvizsgálható a fában található valamennyi pont.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Jellemzők – A problématér minden pontját megvizsgálja Korlátok – A problématér komplexitása – Idő Előnyök – Megtalálja a globális optimumot

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Visszalépéses eljárás A gyökértől indulva az elágazásokban egy előre rögzített sorrendben haladunk rendre a lehetséges irányok egyikében. Először minden elágazásban a sorrend szerinti első lehetséges irányba haladunk, amíg egy levélhez nem érünk. Ekkor megvizsgáljuk, hogy a levél jelentheti-e az optimumot. Ezután az ehhez a levélhez vezető út utolsó elágazásig visszalépünk. Nagy problématérnél nehezen használható.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Elágazás és korlátozás Amennyiben rendelkezésre állnak olyan feltételek vagy megkötések, amelyek segítségével egy adott csúcsot megvizsgálva könnyen eldönthető, hogy az optimum biztosan nem az adott csúcsból kiinduló egyik részfában található, akkor levágjuk ezt a részfát, vagyis az ebben található pontokat nem kell megvizsgálnunk.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Robusztusság Bár a kimerítő keresési módszerek biztosan megtalálják a globális optimumot, valamint a pontok sorra vétele is hasonlít az emberi keresés technikájához, mégis azt kell mondanunk, hogy ezek az eljárások sem bizonyulnak elegendően robusztusnak, ugyanis hatékonyságuknak korlátot szab a problématér komplexitása.

• Gazdaságtudományi Kar • Gazdaságelméleti és Módszertani Intézet Köszönöm a figyelmet!