Gazdasgstatisztika MINTAVTEL LER STATISZTIKAI MUTATSZMOK 2017 oktber 10

Gazdaságstatisztika MINTAVÉTEL, LEÍRÓ STATISZTIKAI MUTATÓSZÁMOK 2017. október 10. , október 12. 2017 ősz Gazdaságstatisztika
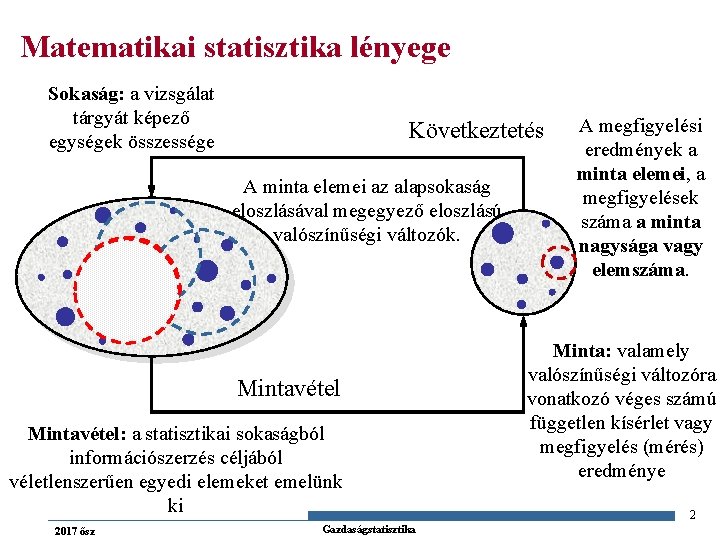
Matematikai statisztika lényege Sokaság: a vizsgálat tárgyát képező egységek összessége Következtetés A minta elemei az alapsokaság eloszlásával megegyező eloszlású valószínűségi változók. Mintavétel: a statisztikai sokaságból információszerzés céljából véletlenszerűen egyedi elemeket emelünk ki 2017 ősz Gazdaságstatisztika A megfigyelési eredmények a minta elemei, a megfigyelések száma a minta nagysága vagy elemszáma. Minta: valamely valószínűségi változóra vonatkozó véges számú független kísérlet vagy megfigyelés (mérés) eredménye 2

Mintavételi és nem mintavételi hiba o o o Adatgyűjtéshez kapcsolódó hibák: pl. definíciós hibák, nemválaszolási hibák, végrehajtási hibák – NEM MINTAVÉTELI HIBA n Védekezési mechanizmus: alkalmazott technikák, technológiák fejlesztése A teljes sokaság megismeréséről való lemondás ára – MINTAVÉTELI HIBA n Védekezési mechanizmus: olyan mintavételi eljárásokat keresünk, hogy ez a lehető legkisebb legyen A mintavételi hiba annál kisebb, minél nagyobb a minta. 3 2017 ősz Gazdaságstatisztika

Statisztikai módszertan ágai n LEÍRÓ vagy DESKRIPTÍV statisztika o n Tömör, számszerű jellemzés: a megfigyelt adatok legjobb megértésére, bemutatására, összefoglalására törekszik. KÖVETKEZTETŐ statisztika o Fő célja a mintából való következtetés, általánosítás a teljes sokaságra vonatkozóan. 2017 ősz Gazdaságstatisztika 4

Leíró statisztika n Főbb területei: 1. adatgyűjtés 2. adatok ábrázolása 3. adatok csoportosítása, osztályozása 4. adatokkal végzett egyszerűbb aritmetikai műveletek 5. eredmények megjelenítése 5 2017 ősz Gazdaságstatisztika

Leíró statisztikai mutatószámok n Helyzetmutatók, középértékek: o n Az eloszlás helyzetét egyetlen, az adatokkal azonos mértékegységű számértékkel jellemzik Ingadozásmutatók: o Az adathalmaz szóródása, változékonysága n n Az adatok egymás közötti különbségei Kitüntetett értéktől való eltérés, ingadozás valamilyen középérték körül 6 2017 ősz Gazdaságstatisztika

Helyzetmutatók (középértékek) n Csoportosításuk: o Helyzeti középértékek: az adatok közötti elhelyezkedésüknél fogva jellemzik a vizsgált gyakorisági eloszlás helyzetét n o Számított középértékek: az adatokkal kapcsolatos számszerű összefüggésük révén jellemzik a vizsgált gyakorisági eloszlás helyzetét n n medián, módusz számtani átlag, mértani átlag, négyzetes átlag, harmonikus átlag Elvárások: o Közepes helyzetűek o Tipikusak o Egyértelműen meghatározhatóak o Könnyen értelmezhetőek 7 2017 ősz Gazdaságstatisztika

Medián n me annak a legelső osztályköznek a sorszáma, amelyre igaz, hogy helyzeti középérték mutató a változó azon számértéke, amelynél az összes előforduló számérték fele A mediánt tartalmazó kisebb, fele pedig nagyobb, így a rangsorba állított sokasági számértékeket két osztály bal végpontja. egyenlő gyakoriságú osztályra bontja Becsülhető osztályközös gyakorisági sorból is: A mediánt tartalmazó osztály hossza. n Előnye: o o n Hátránya: o n Mindig egyértelműen meghatározható Érzéketlen a szélsőértékekre, és nem függ a többi ismérvértéktől sem. Nem használható, ha az adatsorban sok az egyforma ismérvérték Egyéb tulajdonsága: ha 8 2017 ősz Gazdaságstatisztika
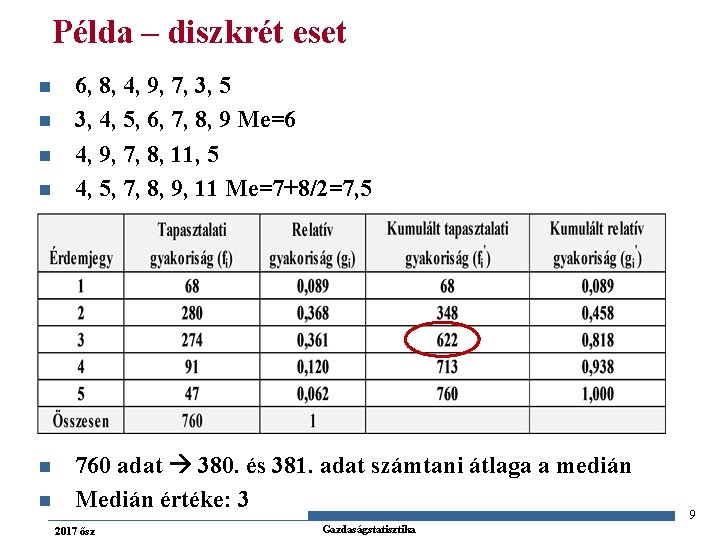
Példa – diszkrét eset n n n 6, 8, 4, 9, 7, 3, 5 3, 4, 5, 6, 7, 8, 9 Me=6 4, 9, 7, 8, 11, 5 4, 5, 7, 8, 9, 11 Me=7+8/2=7, 5 760 adat 380. és 381. adat számtani átlaga a medián Medián értéke: 3 2017 ősz Gazdaságstatisztika 9

Példa – folytonos eset n n 99 adat 50. adat a medián (49 ennél kisebb, 49 ennél nagyobb) Medián értéke: 1, 132% 10 2017 ősz Gazdaságstatisztika
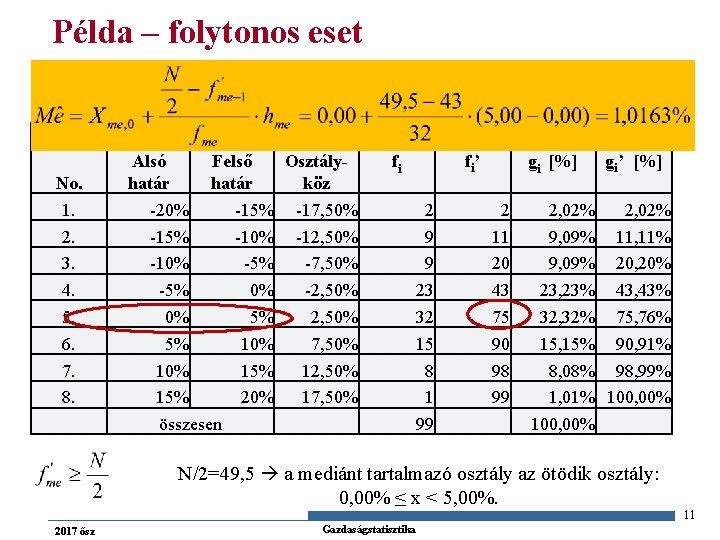
Példa – folytonos eset n Medián becslése osztályközös gyakorisági sorból: No. 1. 2. 3. 4. 5. 6. 7. 8. osztály Alsó Felső Osztályhatár köz -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% N/2=49, 5 a mediánt tartalmazó osztály az ötödik osztály: 0, 00% ≤ x < 5, 00%. 11 2017 ősz Gazdaságstatisztika

Módusz n n n helyzeti középérték, a tipikus ismérvérték diszkrét ismérv esetén a módusz a leggyakrabban előforduló ismérvérték, folytonos ismérv esetén a gyakorisági görbe maximumhelye. Előnye: o o n érzéketlen a szélsőértékekre, nem függ sem az összes, sem a kiugró ismérvértékektől. Hátránya: nem mindig határozható meg egyértelműen, és nem is mindig létezik A móduszt tartalmazó o nagy bizonytalansággal becsülhető o osztály hossza. osztály bal végpontja. n Egyéb tulajdonsága: nyers módusz, osztályköz megválasztása n Becsülhető osztályközös gyakorisági sorból is: mo a legnagyobb gyakoriságú osztály(ok) sorszáma 2017 ősz Gazdaságstatisztika 12

Példa – diszkrét eset n Az elégséges érdemjegy gyakorisága a legnagyobb (280 db), így a módusz értéke 2. 13 2017 ősz Gazdaságstatisztika
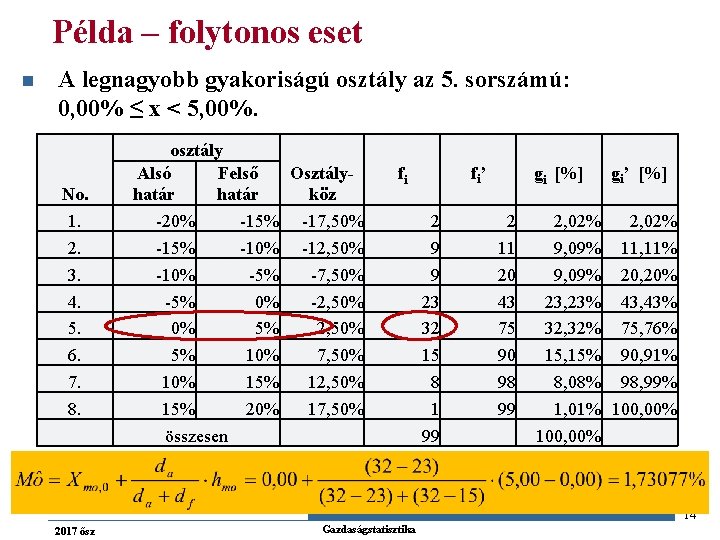
Példa – folytonos eset n A legnagyobb gyakoriságú osztály az 5. sorszámú: 0, 00% ≤ x < 5, 00%. No. 1. 2. 3. 4. 5. 6. 7. 8. osztály Alsó Felső Osztályhatár köz -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% 14 2017 ősz Gazdaságstatisztika

Szorgalmi feladat 1 pont n Egy vasútvonalon egy hétig minden vonaton feljegyezték az utasok számát. Az eredményeket az alábbi táblázat tartalmazza: Utasok száma Vonatok száma 6 12 28 30 16 8 n Számítsa ki a mediánt és a móduszt! 15 2017 ősz Gazdaságstatisztika

Medián és módusz becslése n Utasok száma N fi fi’ 6 6 12 18 28 46 30 76 16 92 8 100 16 2017 ősz Gazdaságstatisztika

Számtani átlag n 17 2017 ősz Gazdaságstatisztika
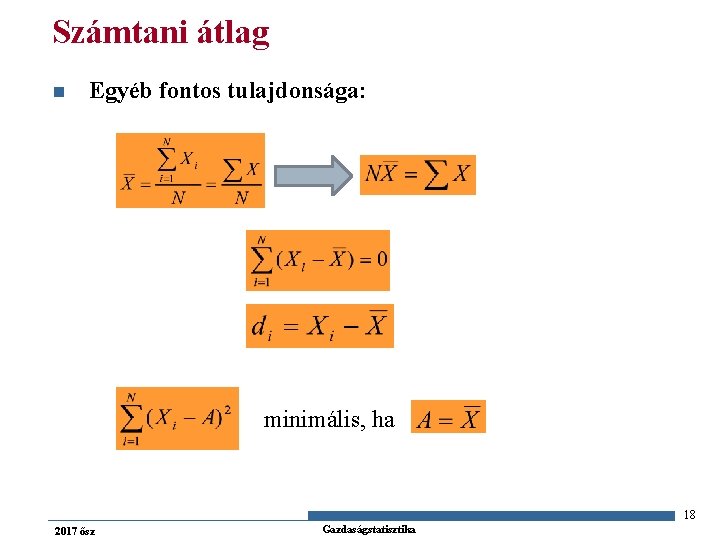
Számtani átlag n Egyéb fontos tulajdonsága: minimális, ha 18 2017 ősz Gazdaságstatisztika
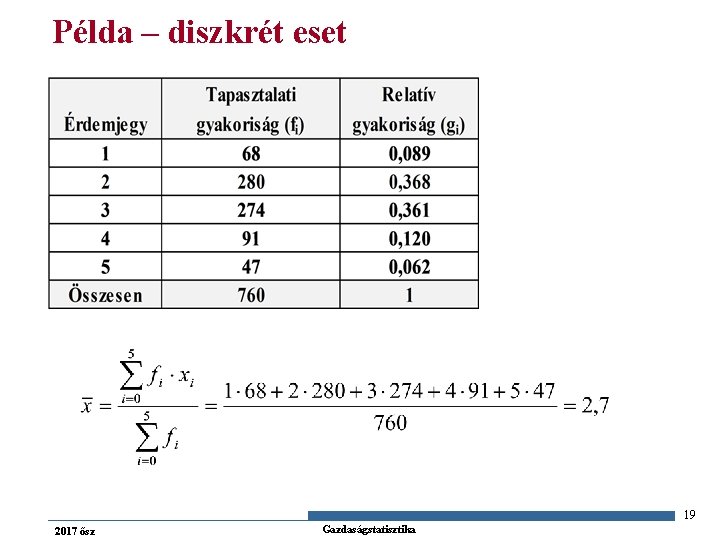
Példa – diszkrét eset 19 2017 ősz Gazdaságstatisztika
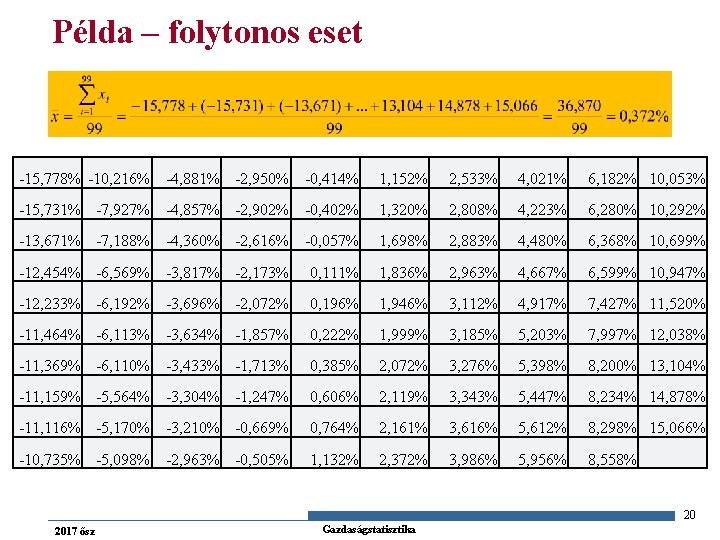
Példa – folytonos eset -15, 778% -10, 216% -4, 881% -2, 950% -0, 414% 1, 152% 2, 533% 4, 021% 6, 182% 10, 053% -15, 731% -7, 927% -4, 857% -2, 902% -0, 402% 1, 320% 2, 808% 4, 223% 6, 280% 10, 292% -13, 671% -7, 188% -4, 360% -2, 616% -0, 057% 1, 698% 2, 883% 4, 480% 6, 368% 10, 699% -12, 454% -6, 569% -3, 817% -2, 173% 0, 111% 1, 836% 2, 963% 4, 667% 6, 599% 10, 947% -12, 233% -6, 192% -3, 696% -2, 072% 0, 196% 1, 946% 3, 112% 4, 917% 7, 427% 11, 520% -11, 464% -6, 113% -3, 634% -1, 857% 0, 222% 1, 999% 3, 185% 5, 203% 7, 997% 12, 038% -11, 369% -6, 110% -3, 433% -1, 713% 0, 385% 2, 072% 3, 276% 5, 398% 8, 200% 13, 104% -11, 159% -5, 564% -3, 304% -1, 247% 0, 606% 2, 119% 3, 343% 5, 447% 8, 234% 14, 878% -11, 116% -5, 170% -3, 210% -0, 669% 0, 764% 2, 161% 3, 616% 5, 612% 8, 298% 15, 066% -10, 735% -5, 098% -2, 963% -0, 505% 1, 132% 2, 372% 3, 986% 5, 956% 8, 558% 20 2017 ősz Gazdaságstatisztika
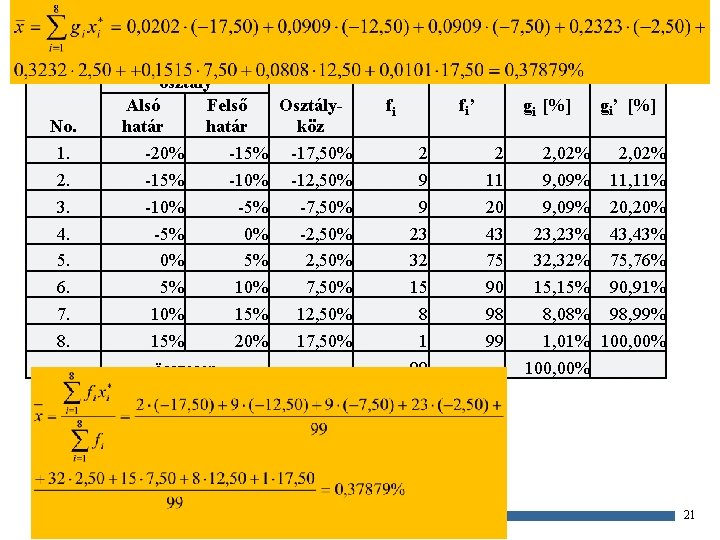
Példa – folytonos példa No. 1. 2. 3. 4. 5. 6. 7. 8. osztály Osztály. Alsó Felső köz határ -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% 21 2017 ősz Gazdaságstatisztika

Harmonikus átlag n számított középértékmutató, az a szám, amellyel az átlagolandó értékeket helyettesítve azok reciprokainak összege változatlan marad n Alkalmazása: ha az értékek reciprokainak összege értelmezhető, leíró statisztikai viszonyszámok és indexszámítás 22 2017 ősz Gazdaságstatisztika

Mértani átlag n számított középértékmutató, az a szám, amellyel az átlagolandó értékeket helyettesítve azok szorzata változatlan marad n Alkalmazása: o ha az értékek szorzata értelmezhető, illetve az átlagolandó értékek exponenciálisan nőnek vagy csökkennek o az időbeli fejlődés átlagos ütemének vizsgálatakor n o Pl. populációk egyedszáma idősor-elemzés 23 2017 ősz Gazdaságstatisztika

Négyzetes átlag n számított középérték-mutató, az a szám, amellyel az átlagolandó értékeket helyettesítve azok négyzetösszege változatlan marad n Hátránya: a kiugróan magas értékekre érzékenyen reagál Alkalmazása: o ha az előjeleknek nincs jelentősége o szórásszámítás n 24 2017 ősz Gazdaságstatisztika

Kvantilisek n n a rangsorban olyan osztópontok (osztályhatárok), amelyek egyenlő relatív gyakoriságokat fognak közre Az Xi/k i-edik k-ad rendű kvantilis az a szám, amelynél az összes előforduló ismérvértékek i/k-ad része kisebb, (1 -i/k)-ad része pedig nagyobb, ahol k≥ 2 és i=1, 2 , …, k-1. 25 2017 ősz Gazdaságstatisztika
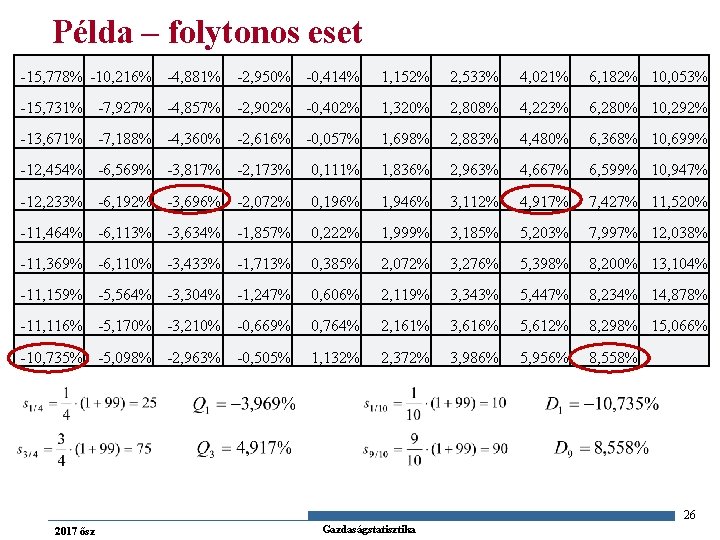
Példa – folytonos eset -15, 778% -10, 216% -4, 881% -2, 950% -0, 414% 1, 152% 2, 533% 4, 021% 6, 182% 10, 053% -15, 731% -7, 927% -4, 857% -2, 902% -0, 402% 1, 320% 2, 808% 4, 223% 6, 280% 10, 292% -13, 671% -7, 188% -4, 360% -2, 616% -0, 057% 1, 698% 2, 883% 4, 480% 6, 368% 10, 699% -12, 454% -6, 569% -3, 817% -2, 173% 0, 111% 1, 836% 2, 963% 4, 667% 6, 599% 10, 947% -12, 233% -6, 192% -3, 696% -2, 072% 0, 196% 1, 946% 3, 112% 4, 917% 7, 427% 11, 520% -11, 464% -6, 113% -3, 634% -1, 857% 0, 222% 1, 999% 3, 185% 5, 203% 7, 997% 12, 038% -11, 369% -6, 110% -3, 433% -1, 713% 0, 385% 2, 072% 3, 276% 5, 398% 8, 200% 13, 104% -11, 159% -5, 564% -3, 304% -1, 247% 0, 606% 2, 119% 3, 343% 5, 447% 8, 234% 14, 878% -11, 116% -5, 170% -3, 210% -0, 669% 0, 764% 2, 161% 3, 616% 5, 612% 8, 298% 15, 066% -10, 735% -5, 098% -2, 963% -0, 505% 1, 132% 2, 372% 3, 986% 5, 956% 8, 558% 26 2017 ősz Gazdaságstatisztika
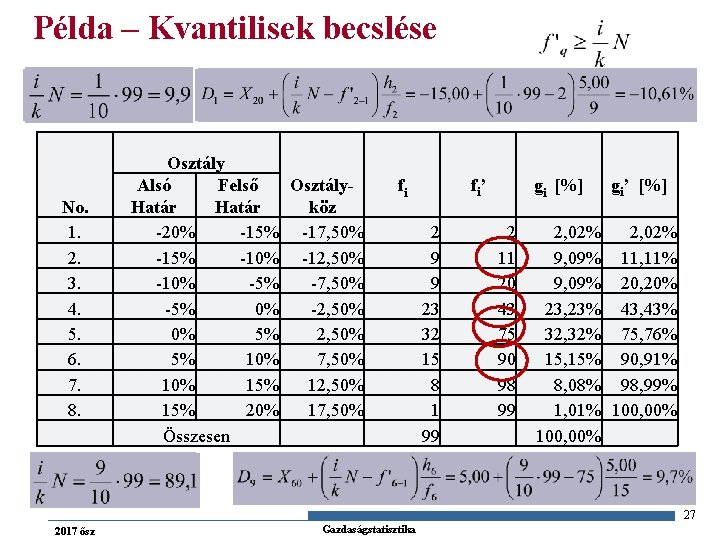
Példa – Kvantilisek becslése No. 1. 2. 3. 4. 5. 6. 7. 8. Osztály. Alsó Felső köz Határ -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% Összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% 27 2017 ősz Gazdaságstatisztika

Ingadozásmutatók (szóródásmutatók) n Csoportosításuk: o o Az adathalmazban szereplő értékek változékonyságát n az egyes értékek egymás közötti különbségein, vagy n egyes értékeknek egy kitüntetett értéktől (középérték) való eltérésein keresztül ragadja meg. Mértékegységüket tekintve: n Abszolút mutatók: mértékegysége megegyezik az alapadatokéval n Relatív mutatók: mértékegység nélküli [%] 28 2017 ősz Gazdaságstatisztika

Terjedelem n n a szóródást az adathalmazban szereplő legnagyobb és legkisebb adat különbségeként jellemzi abszolút ingadozásmutató n Előnye: a könnyű számítás Hátránya: értéke csak a két legszélsőségesebb ismérvértéktől függ, amelyeket sokszor a véletlen szeszélyeinek köszönhetünk. n Interkvantilis terjedelem n o o csökkenti a véletlen szélsőértékeket (legkisebb és legnagyobb értéket) alakító szerepét az adathalmaz két szélső k-adrendű kvantilisének különbsége 29 2017 ősz Gazdaságstatisztika
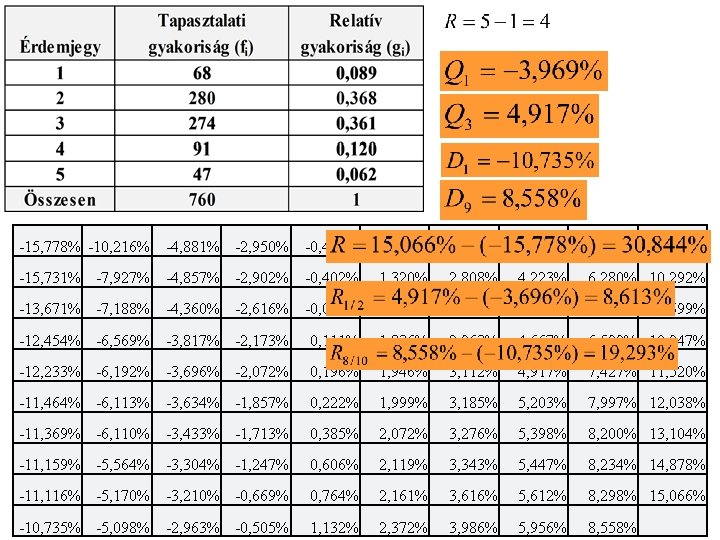
-15, 778% -10, 216% -4, 881% -2, 950% -0, 414% 1, 152% 2, 533% 4, 021% 6, 182% 10, 053% -15, 731% -7, 927% -4, 857% -2, 902% -0, 402% 1, 320% 2, 808% 4, 223% 6, 280% 10, 292% -13, 671% -7, 188% -4, 360% -2, 616% -0, 057% 1, 698% 2, 883% 4, 480% 6, 368% 10, 699% -12, 454% -6, 569% -3, 817% -2, 173% 0, 111% 1, 836% 2, 963% 4, 667% 6, 599% 10, 947% -12, 233% -6, 192% -3, 696% -2, 072% 0, 196% 1, 946% 3, 112% 4, 917% 7, 427% 11, 520% -11, 464% -6, 113% -3, 634% -1, 857% 0, 222% 1, 999% 3, 185% 5, 203% 7, 997% 12, 038% -11, 369% -6, 110% -3, 433% -1, 713% 0, 385% 2, 072% 3, 276% 5, 398% 8, 200% 13, 104% -11, 159% -5, 564% -3, 304% -1, 247% 0, 606% 2, 119% 3, 343% 5, 447% 8, 234% 14, 878% -11, 116% -5, 170% -3, 210% -0, 669% 0, 764% 2, 161% 3, 616% 5, 612% 8, 298% 15, 066% -10, 735% 2017 ősz -5, 098% -2, 963% -0, 505% 1, 132% 2, 372% Gazdaságstatisztika 3, 986% 5, 956% 8, 558% 30

(Korrigált) tapasztalati szórás n n n a szóródást az alapadatoknak egy kitüntetett értéktől (számtani átlagtól) való eltérésein keresztül méri, abszolút ingadozásmutató A szórás az egyes Xi ismérvértékek átlagtól vett di eltéréseinek négyzetes átlaga: azt mutatja, hogy az egyes értékek átlagosan mennyire térnek el a számtani átlagtól. Olyan átlagos hiba, amit akkor követünk el, ha minden alapadatot a számtani átlaggal helyettesítünk. A számtani átlag tulajdonsága szerint ez a hiba minimális. 31 2017 ősz Gazdaságstatisztika
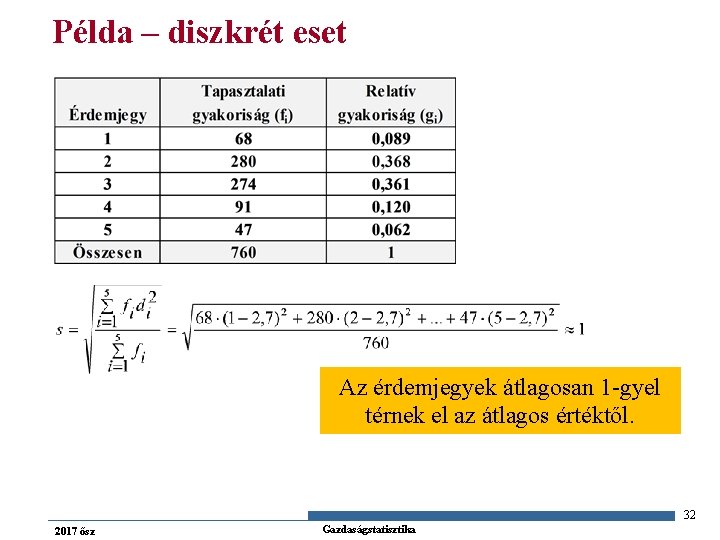
Példa – diszkrét eset Az érdemjegyek átlagosan 1 -gyel térnek el az átlagos értéktől. 32 2017 ősz Gazdaságstatisztika
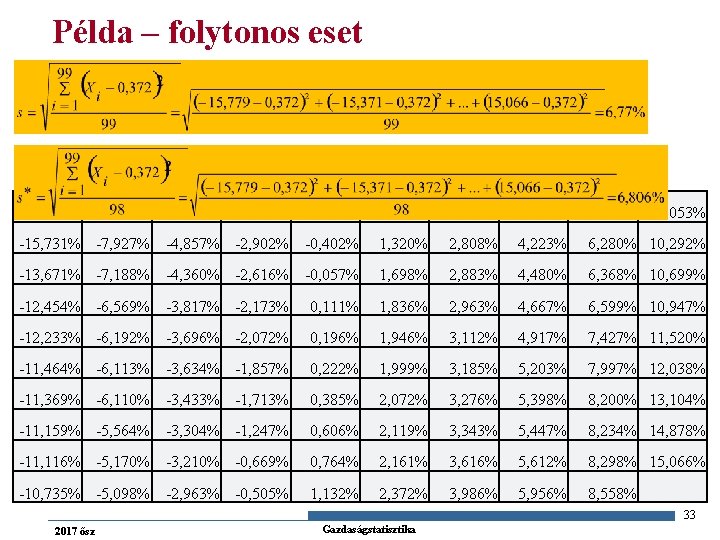
Példa – folytonos eset -15, 778% -10, 216% -4, 881% -2, 950% -0, 414% 1, 152% 2, 533% 4, 021% 6, 182% 10, 053% -15, 731% -7, 927% -4, 857% -2, 902% -0, 402% 1, 320% 2, 808% 4, 223% 6, 280% 10, 292% -13, 671% -7, 188% -4, 360% -2, 616% -0, 057% 1, 698% 2, 883% 4, 480% 6, 368% 10, 699% -12, 454% -6, 569% -3, 817% -2, 173% 0, 111% 1, 836% 2, 963% 4, 667% 6, 599% 10, 947% -12, 233% -6, 192% -3, 696% -2, 072% 0, 196% 1, 946% 3, 112% 4, 917% 7, 427% 11, 520% -11, 464% -6, 113% -3, 634% -1, 857% 0, 222% 1, 999% 3, 185% 5, 203% 7, 997% 12, 038% -11, 369% -6, 110% -3, 433% -1, 713% 0, 385% 2, 072% 3, 276% 5, 398% 8, 200% 13, 104% -11, 159% -5, 564% -3, 304% -1, 247% 0, 606% 2, 119% 3, 343% 5, 447% 8, 234% 14, 878% -11, 116% -5, 170% -3, 210% -0, 669% 0, 764% 2, 161% 3, 616% 5, 612% 8, 298% 15, 066% -10, 735% -5, 098% -2, 963% -0, 505% 1, 132% 2, 372% 3, 986% 5, 956% 8, 558% 33 2017 ősz Gazdaságstatisztika
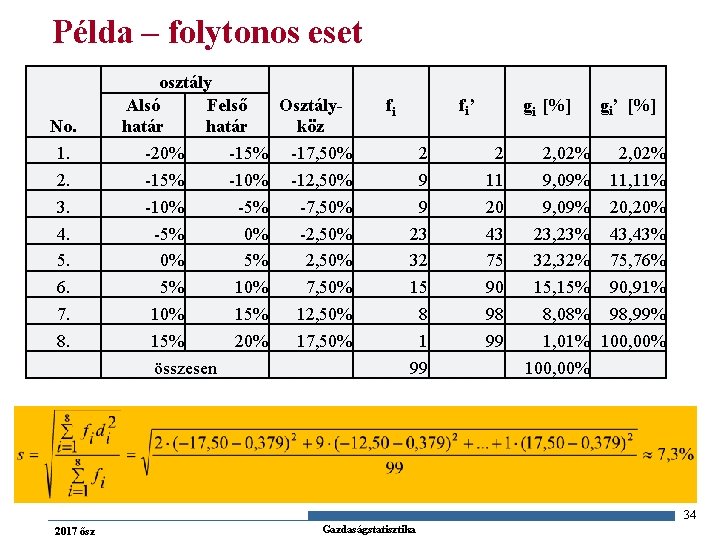
Példa – folytonos eset No. 1. 2. 3. 4. 5. 6. 7. 8. osztály Osztály. Alsó Felső köz határ -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% 34 2017 ősz Gazdaságstatisztika

Szorgalmi feladat 1 pont n Egy vasútvonalon egy hétig minden vonaton feljegyezték az utasok számát. Az eredményeket az alábbi táblázat tartalmazza: Utasok száma Vonatok száma 6 12 28 30 16 8 n Számítsa ki a szórást illetve a korrigált tapasztalati szórást! 35 2017 ősz Gazdaságstatisztika

Szórás, korrigált tapasztalati szórás n Számtani átlag meghatározása n Eltérés-négyzetösszeg meghatározása n Tapasztalati szórás n Korrigált tapasztalati szórás 36 2017 ősz Gazdaságstatisztika

Átlagos abszolút eltérés (Δ) n n n A szóródást az értékeknek egy kitüntetett értéktől való eltéréseire támaszkodva jellemzi abszolút ingadozásmutató Az egyes ismérvértékek és a számtani átlag különbségeinek abszolút értékeiből számított számtani átlag 37 2017 ősz Gazdaságstatisztika
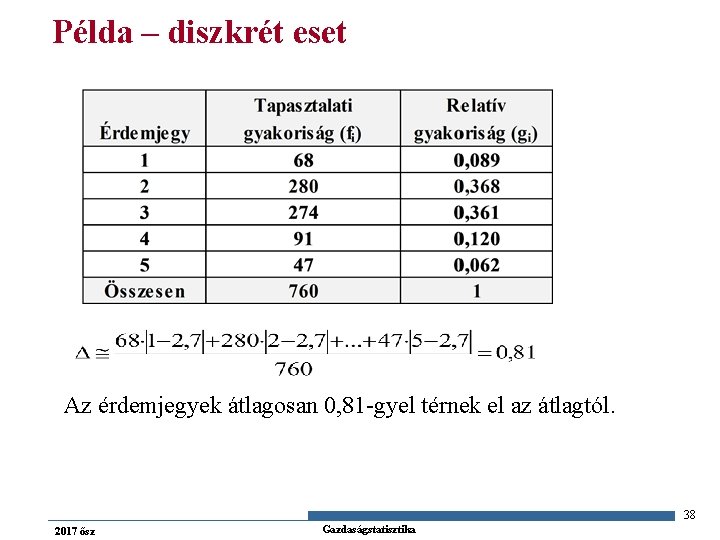
Példa – diszkrét eset Az érdemjegyek átlagosan 0, 81 -gyel térnek el az átlagtól. 38 2017 ősz Gazdaságstatisztika
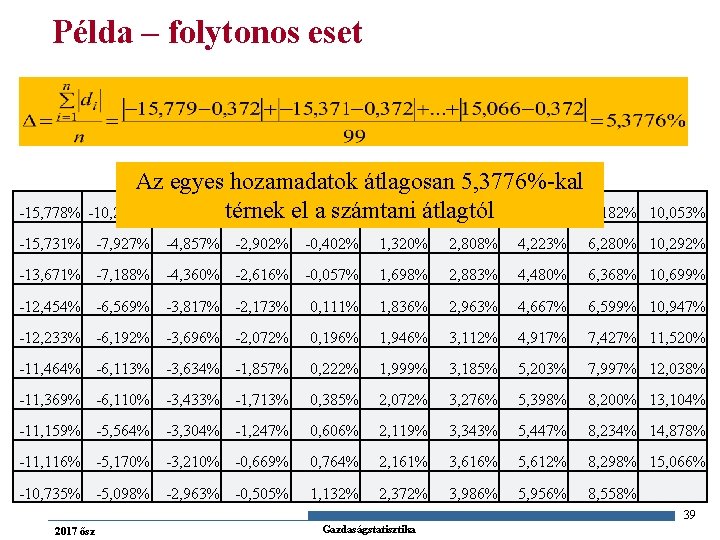
Példa – folytonos eset Az egyes hozamadatok átlagosan 5, 3776%-kal -15, 778% -10, 216% -4, 881% térnek el a számtani átlagtól -2, 950% -0, 414% 1, 152% 2, 533% 4, 021% 6, 182% 10, 053% -15, 731% -7, 927% -4, 857% -2, 902% -0, 402% 1, 320% 2, 808% 4, 223% 6, 280% 10, 292% -13, 671% -7, 188% -4, 360% -2, 616% -0, 057% 1, 698% 2, 883% 4, 480% 6, 368% 10, 699% -12, 454% -6, 569% -3, 817% -2, 173% 0, 111% 1, 836% 2, 963% 4, 667% 6, 599% 10, 947% -12, 233% -6, 192% -3, 696% -2, 072% 0, 196% 1, 946% 3, 112% 4, 917% 7, 427% 11, 520% -11, 464% -6, 113% -3, 634% -1, 857% 0, 222% 1, 999% 3, 185% 5, 203% 7, 997% 12, 038% -11, 369% -6, 110% -3, 433% -1, 713% 0, 385% 2, 072% 3, 276% 5, 398% 8, 200% 13, 104% -11, 159% -5, 564% -3, 304% -1, 247% 0, 606% 2, 119% 3, 343% 5, 447% 8, 234% 14, 878% -11, 116% -5, 170% -3, 210% -0, 669% 0, 764% 2, 161% 3, 616% 5, 612% 8, 298% 15, 066% -10, 735% -5, 098% -2, 963% -0, 505% 1, 132% 2, 372% 3, 986% 5, 956% 8, 558% 39 2017 ősz Gazdaságstatisztika
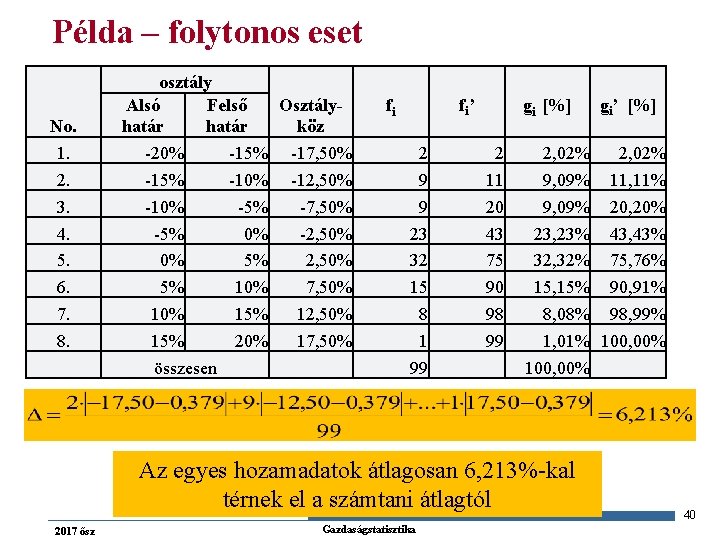
Példa – folytonos eset No. 1. 2. 3. 4. 5. 6. 7. 8. osztály Osztály. Alsó Felső köz határ -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% Az egyes hozamadatok átlagosan 6, 213%-kal térnek el a számtani átlagtól 2017 ősz Gazdaságstatisztika gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% 40

Átlagos abszolút különbség (G) n n A szóródást az ismérvértékek egymás közötti különbségein keresztül méri, abszolút ingadozásmutató A minden lehetséges módon párba állított ismérvértékek különbségeinek abszolút értékéből számított számtani átlag. Kényelmetlen a számítása Alkalmazási területe: koncentráció elemzés 41 2017 ősz Gazdaságstatisztika

Példa n n Véletlenszerűen kiválasztunk 5 hallgatót, és kiszámítjuk a Gazdaságstatisztika tárgy 3 zh-ján elért eredményük átlagos abszolút különbségét. Az elért pontok: 45, 52, 76, 87, 92 45 52 76 87 92 45 0 7 31 42 47 52 7 0 24 35 40 76 31 24 0 11 16 87 42 35 11 0 5 92 47 40 16 5 0 Az 5 hallgató zh-n elért pontja átlagosan 25, 8 ponttal tér el egymástól 42 2017 ősz Gazdaságstatisztika

Relatív szórás n n n relatív ingadozásmutató az ismérvértékek átlagtól vett átlagos eltérése százalékos formában kifejezve a szórás és a számtani átlag hányadosa, csak pozitív értékű alapadatok esetében számítható: minél kisebb a relatív szórás, a számtani átlag annál jobban jellemzi az alapadatokat Alkalmazása: különböző sokaságok vagy ismérvek szóródásának összehasonlítására használják 43 2017 ősz Gazdaságstatisztika

Köszönöm a figyelmet! Árva Gábor 2017 ősz Gazdaságstatisztika
- Slides: 44