Gazdasgstatisztika Ler statisztika gyakorl feladatok 2015 oktber 15

Gazdaságstatisztika Leíró statisztika gyakorló feladatok 2015. október 15.
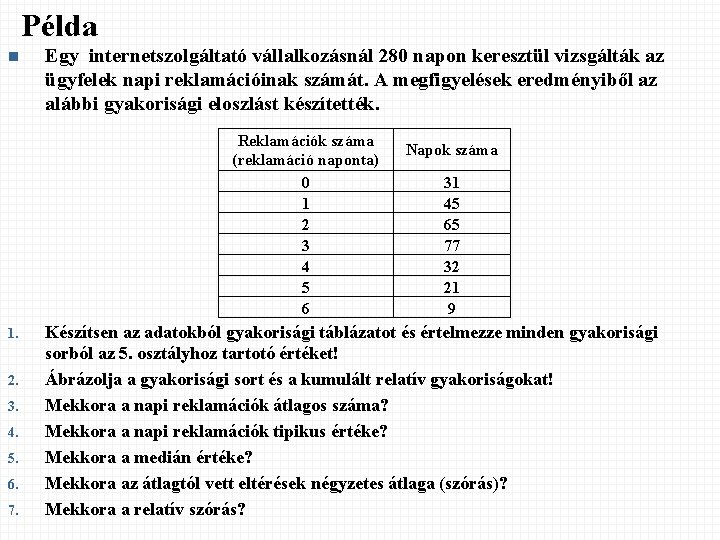
Példa n Egy internetszolgáltató vállalkozásnál 280 napon keresztül vizsgálták az ügyfelek napi reklamációinak számát. A megfigyelések eredményiből az alábbi gyakorisági eloszlást készítették. Reklamációk száma (reklamáció naponta) 0 1 2 3 4 5 6 1. 2. 3. 4. 5. 6. 7. Napok száma 31 45 65 77 32 21 9 Készítsen az adatokból gyakorisági táblázatot és értelmezze minden gyakorisági sorból az 5. osztályhoz tartotó értéket! Ábrázolja a gyakorisági sort és a kumulált relatív gyakoriságokat! Mekkora a napi reklamációk átlagos száma? Mekkora a napi reklamációk tipikus értéke? Mekkora a medián értéke? Mekkora az átlagtól vett eltérések négyzetes átlaga (szórás)? Mekkora a relatív szórás?
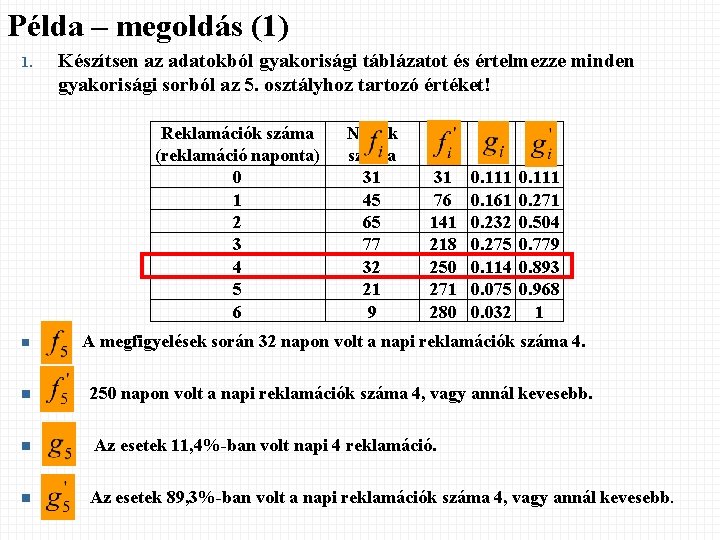
Példa – megoldás (1) 1. Készítsen az adatokból gyakorisági táblázatot és értelmezze minden gyakorisági sorból az 5. osztályhoz tartozó értéket! Reklamációk száma (reklamáció naponta) 0 1 2 3 4 5 6 Napok száma 31 45 65 77 32 21 9 31 76 141 218 250 271 280 0. 111 0. 161 0. 232 0. 275 0. 114 0. 075 0. 032 0. 111 0. 271 0. 504 0. 779 0. 893 0. 968 1 n A megfigyelések során 32 napon volt a napi reklamációk száma 4. n 250 napon volt a napi reklamációk száma 4, vagy annál kevesebb. n Az esetek 11, 4%-ban volt napi 4 reklamáció. n Az esetek 89, 3%-ban volt a napi reklamációk száma 4, vagy annál kevesebb.
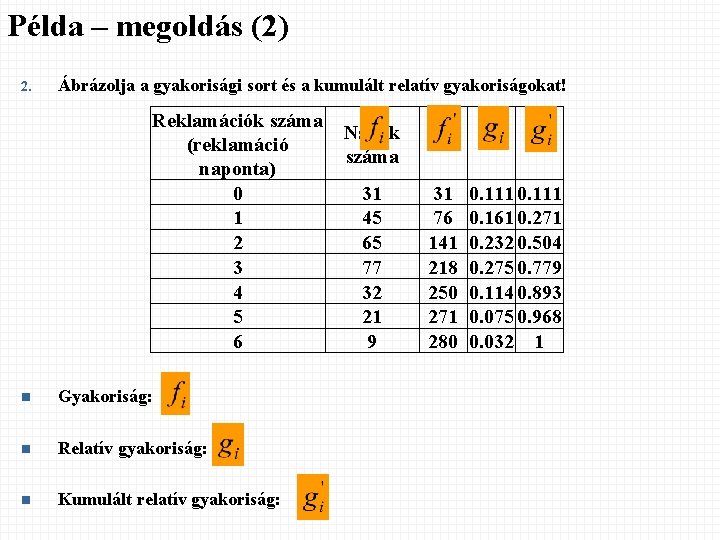
Példa – megoldás (2) 2. Ábrázolja a gyakorisági sort és a kumulált relatív gyakoriságokat! Reklamációk száma Napok (reklamáció száma naponta) 0 31 1 45 2 65 3 77 4 32 5 21 6 9 n Gyakoriság: n Relatív gyakoriság: n Kumulált relatív gyakoriság: 31 76 141 218 250 271 280 0. 111 0. 161 0. 271 0. 232 0. 504 0. 275 0. 779 0. 114 0. 893 0. 075 0. 968 0. 032 1
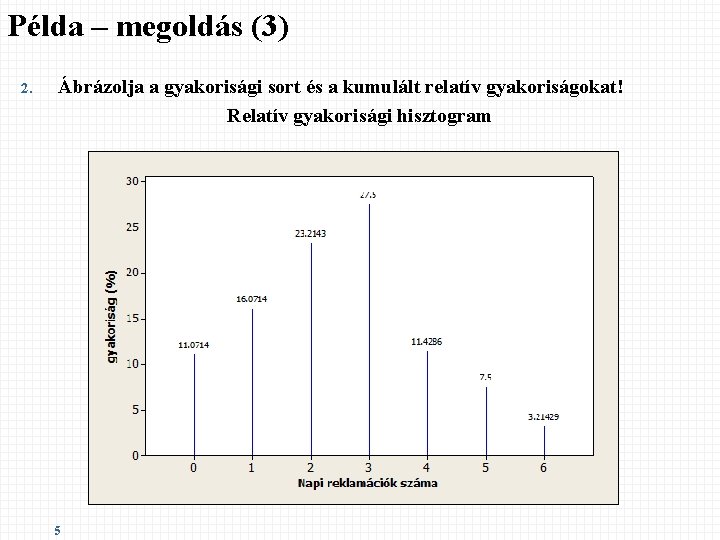
Példa – megoldás (3) 2. Ábrázolja a gyakorisági sort és a kumulált relatív gyakoriságokat! Relatív gyakorisági hisztogram 5
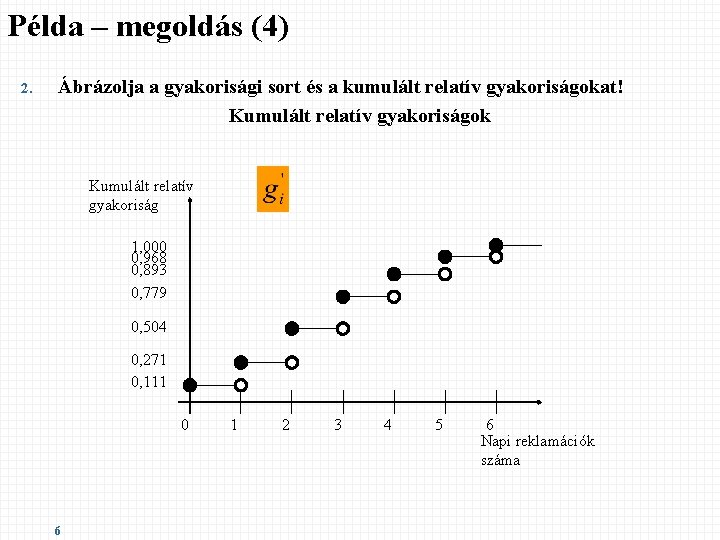
Példa – megoldás (4) 2. Ábrázolja a gyakorisági sort és a kumulált relatív gyakoriságokat! Kumulált relatív gyakoriságok Kumulált relatív gyakoriság 1, 000 0, 968 0, 893 0, 779 0, 504 0, 271 0, 111 0 6 1 2 3 4 5 6 Napi reklamációk száma

Példa – megoldás (5) 3. Mekkora a napi reklamációk átlagos száma? Reklamációk száma (reklamáció naponta) 0 1 2 3 4 5 6 Napok száma 31 45 65 77 32 21 9 31 76 141 218 250 271 280 0. 111 0. 161 0. 232 0. 275 0. 114 0. 075 0. 032 0. 111 0. 271 0. 504 0. 779 0. 893 0. 968 1

Példa – megoldás (6) Mekkora a napi reklamációk tipikus értéke? A napi reklamációk tipikus értéke a módusz. 4. Reklamációk száma (reklamáció naponta) 0 1 2 3 4 5 6 Napok száma 31 45 65 77 32 21 9 A módusz értéke 3. Azért tipikus, mert ez a leggyakoribb érték. 31 76 141 218 250 271 280 0. 111 0. 161 0. 232 0. 275 0. 114 0. 075 0. 032 0. 111 0. 271 0. 504 0. 779 0. 893 0. 968 1

Példa – megoldás (7) 5. Mekkora a medián értéke? Reklamációk száma (reklamáció naponta) 0 1 2 3 4 5 6 Napok száma 31 45 65 77 32 21 9 31 76 141 218 250 271 280 0. 111 0. 161 0. 232 0. 275 0. 114 0. 075 0. 032 0. 111 0. 271 0. 504 0. 779 0. 893 0. 968 1 Páros számú adat esetén a sorba rendezett adatok között a két középső átlaga a medián. Esetünkben a 140. és a 141. adat a növekvő sorrendbe rendezett adatok között a két középső. E két adat értéke rendre a 2 és a 2. Ezért a medián értéke 2. Miért nem ezzel számoltunk?

Példa – megoldás (8) 6. Mekkora az átlagtól vett eltérések négyzetes átlaga (szórás)? Reklamációk száma (reklamáció naponta) 0 1 2 3 4 5 6 7. Mekkora a relatív szórás? 10 Napok száma 31 45 65 77 32 21 9 31 76 141 218 250 271 280 0. 111 0. 161 0. 232 0. 275 0. 114 0. 075 0. 032 0. 111 0. 271 0. 504 0. 779 0. 893 0. 968 1

Példa n 1. 2. 3. 4. 5. 6. 7. 8. Egy áramszolgáltatónál 650 megfigyelést végeztek a szolgáltatásban bekövetkező áramkimaradásokra vonatkozóan. A megfigyelések eredményit az alábbi táblázatban rögzítették. Áramkimaradások időtartama (perc) száma [0; 10) 40 [10; 20) 190 [20; 30) 350 [30; 40) 40 [40; 50) 20 [50; 60) 10 Készítsen az adatokból gyakorisági táblázatot és értelmezze minden gyakorisági sorból a 4. osztályhoz tartotó értéket! Ábrázolja az áramkimaradások időtartam szerinti megoszlását és a tapasztalati eloszlásképet! Mekkora az áramkimaradások átlagos időtartama? Mekkora a tipikusnak tekinthető áramkimaradás időtartama? Becsülje meg és értelmezze a mediánt! Adjon becslést a szórásra! Mekkora a relatív szórás? Becsülje meg az alsó és felső kvartiliseket és deciliseket!
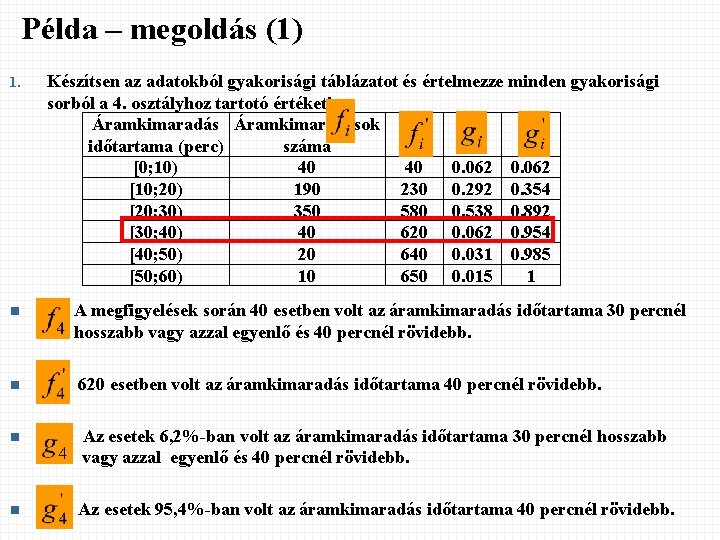
Példa – megoldás (1) 1. Készítsen az adatokból gyakorisági táblázatot és értelmezze minden gyakorisági sorból a 4. osztályhoz tartotó értéket! Áramkimaradások időtartama (perc) száma [0; 10) 40 40 0. 062 [10; 20) 190 230 0. 292 0. 354 [20; 30) 350 580 0. 538 0. 892 [30; 40) 40 620 0. 062 0. 954 [40; 50) 20 640 0. 031 0. 985 [50; 60) 10 650 0. 015 1 n A megfigyelések során 40 esetben volt az áramkimaradás időtartama 30 percnél hosszabb vagy azzal egyenlő és 40 percnél rövidebb. n 620 esetben volt az áramkimaradás időtartama 40 percnél rövidebb. n Az esetek 6, 2%-ban volt az áramkimaradás időtartama 30 percnél hosszabb vagy azzal egyenlő és 40 percnél rövidebb. n Az esetek 95, 4%-ban volt az áramkimaradás időtartama 40 percnél rövidebb.

Példa – megoldás (2) 2. Ábrázolja az áramkimaradások időtartam szerinti megoszlását és a tapasztalati eloszlásképet! Áramkimaradás időtartama dások száma (perc) [0; 10) 40 [10; 20) 190 [20; 30) 350 [30; 40) 40 [40; 50) 20 [50; 60) 10 40 230 580 620 640 650 0. 062 0. 292 0. 538 0. 062 0. 031 0. 015 0. 062 0. 354 0. 892 0. 954 0. 985 1 Időtartam szerinti megoszlás (relatív gyakorisági hisztogram ) 10 20 30 40 50 60 Áramkimaradások időtartama (perc)
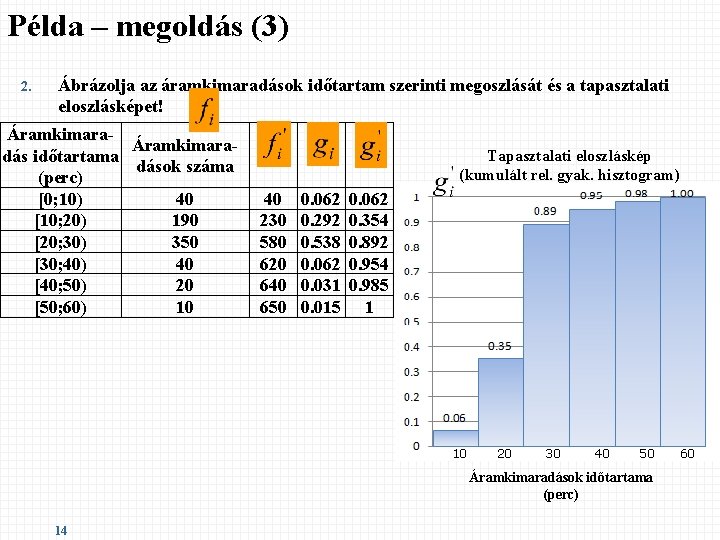
Példa – megoldás (3) 2. Ábrázolja az áramkimaradások időtartam szerinti megoszlását és a tapasztalati eloszlásképet! Áramkimaradás időtartama dások száma (perc) [0; 10) 40 [10; 20) 190 [20; 30) 350 [30; 40) 40 [40; 50) 20 [50; 60) 10 40 230 580 620 640 650 0. 062 0. 292 0. 538 0. 062 0. 031 0. 015 0. 062 0. 354 0. 892 0. 954 0. 985 1 Tapasztalati eloszláskép (kumulált rel. gyak. hisztogram) 10 20 30 40 50 Áramkimaradások időtartama (perc) 14 60
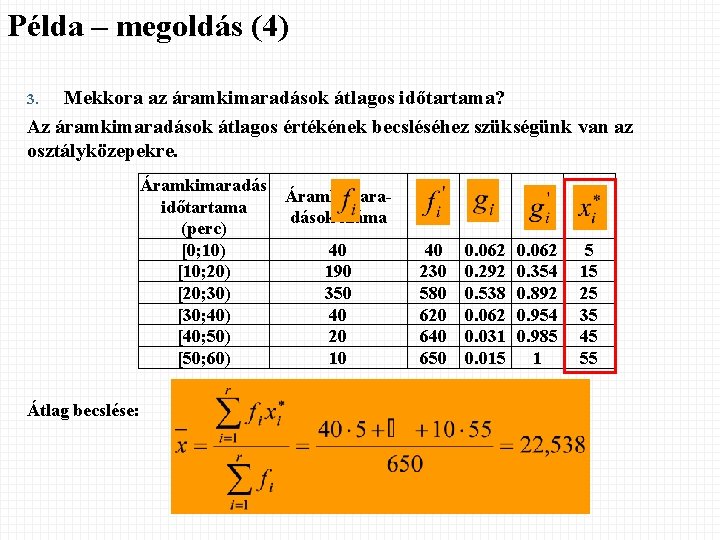
Példa – megoldás (4) Mekkora az áramkimaradások átlagos időtartama? Az áramkimaradások átlagos értékének becsléséhez szükségünk van az osztályközepekre. 3. Áramkimaradás Áramkimaraidőtartama dások száma (perc) [0; 10) 40 [10; 20) 190 [20; 30) 350 [30; 40) 40 [40; 50) 20 [50; 60) 10 Átlag becslése: 40 230 580 620 640 650 0. 062 0. 292 0. 538 0. 062 0. 031 0. 015 0. 062 0. 354 0. 892 0. 954 0. 985 1 5 15 25 35 45 55
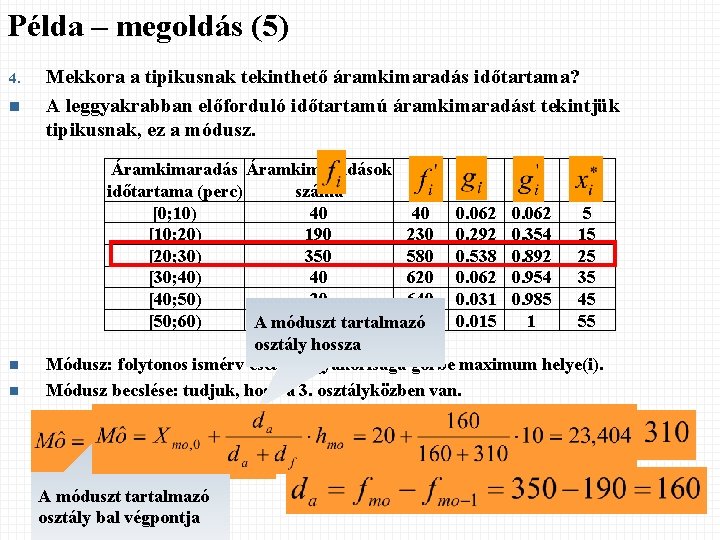
Példa – megoldás (5) 4. n n n Mekkora a tipikusnak tekinthető áramkimaradás időtartama? A leggyakrabban előforduló időtartamú áramkimaradást tekintjük tipikusnak, ez a módusz. Áramkimaradások időtartama (perc) száma [0; 10) 40 40 0. 062 5 [10; 20) 190 230 0. 292 0. 354 15 [20; 30) 350 580 0. 538 0. 892 25 [30; 40) 40 620 0. 062 0. 954 35 [40; 50) 20 640 0. 031 0. 985 45 [50; 60) 10 650 0. 015 1 55 A móduszt tartalmazó osztály hossza Módusz: folytonos ismérv esetén a gyakorisága görbe maximum helye(i). Módusz becslése: tudjuk, hogy a 3. osztályközben van. A móduszt tartalmazó osztály bal végpontja 16

Példa – megoldás (6) 5. Becsülje meg és értelmezze a mediánt! Áramkimaradások időtartama (perc) száma [0; 10) 40 40 0. 062 [10; 20) 190 230 0. 292 [20; 30) 350 580 0. 538 [30; 40) 40 620 0. 062 [40; 50) 20 640 0. 031 A mediánt tartalmazó [50; 60) 10 650 0. 015 osztály hossza 0. 062 0. 354 0. 892 0. 954 0. 985 1 5 15 25 35 45 55 a megfigyelések száma: 650 A mediánt tartalmazó osztály alsó osztályhatárának értéke 17 Az első olyan osztályköz sorszáma, amelyhez tartozó kumulált gyakoriság nagyobb vagy egyenlő, mint a megfigyelések számának fele. Most a 3. osztály.

Példa – megoldás (7) 6. Adjon becslést a szórásra! Áramkimaradások időtartama (perc) száma [0; 10) 40 [10; 20) 190 [20; 30) 350 [30; 40) 40 [40; 50) 20 [50; 60) 10 7. Mekkora a relatív szórás? 18 40 230 580 620 640 650 0. 062 0. 292 0. 538 0. 062 0. 031 0. 015 0. 062 0. 354 0. 892 0. 954 0. 985 1 5 15 25 35 45 55

Példa – megoldás (8) 8. Számszerűsítsen alakmutatókat! Áramkimaradások időtartama (perc) száma [0; 10) 40 40 [10; 20) 190 230 [20; 30) 350 580 [30; 40) 40 620 [40; 50) 20 640 [50; 60) 10 650 19 0. 062 0. 292 0. 538 0. 062 0. 031 0. 015 0. 062 0. 354 0. 892 0. 954 0. 985 1 5 15 25 35 45 55
- Slides: 19