Gausss Law Chapter 21 Summary Sheet 2 EXERCISE

Gauss’s Law Chapter 21 Summary Sheet 2

EXERCISE: Draw electric field vectors due to the point charge shown, at A, B and C C . B . + Now draw field lines. . A

In this chapter you’ll learn • • To represent electric fields using field-line diagrams To explain Gauss’s law and how it relates to Coulomb’s law To calculate the electric fields for symmetric charge distributions using Gauss’s law (EASY!) To describe the behavior of charge on conductors in electrostatic equilibrium

21. 1 Electric Field Lines NB For electric field at P draw tail of vector at point P We can draw a vector at each point around a charged object - • direction of E is tangent to field line (in same direction as F) • E is larger where field lines are closer together • electric field lines extend away from positive charge (where they originate) and towards negative charge (where they terminate)

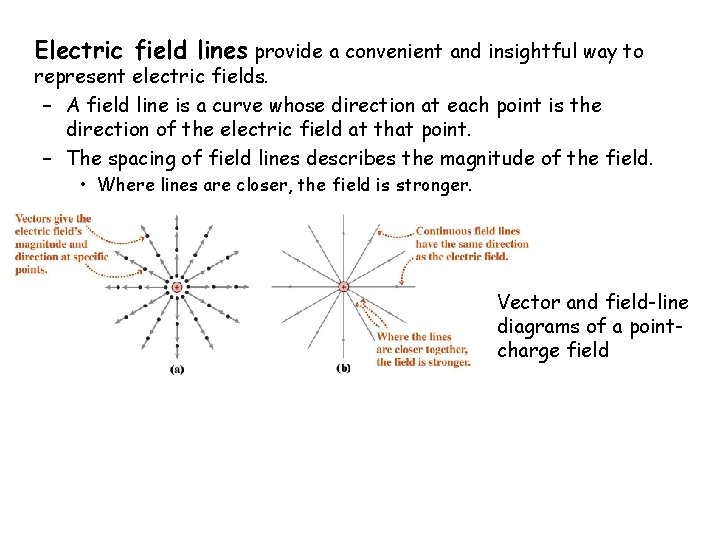
Electric field lines provide a convenient and insightful way to represent electric fields. – A field line is a curve whose direction at each point is the direction of the electric field at that point. – The spacing of field lines describes the magnitude of the field. • Where lines are closer, the field is stronger. Vector and field-line diagrams of a pointcharge field

The field lines for two equal positive charges The field lines for two charges equal in magnitude but opposite in sign – an electric dipole NB the electric field vector at a point is tangent to the field line through the point

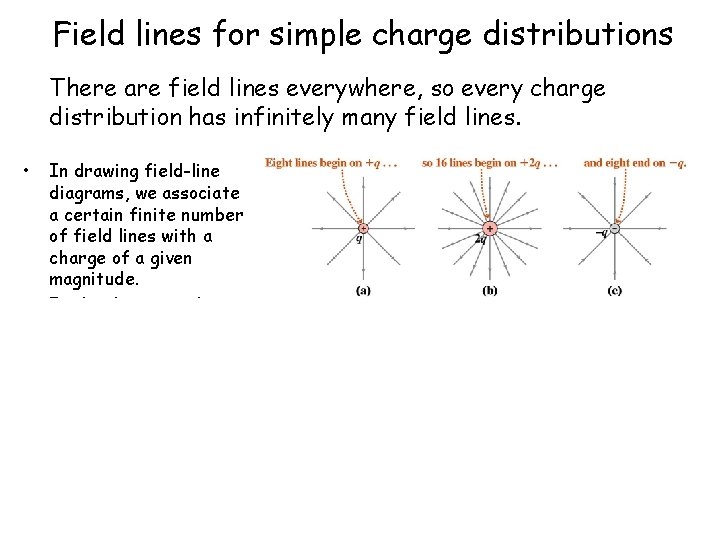
Field lines for simple charge distributions There are field lines everywhere, so every charge distribution has infinitely many field lines. • • • In drawing field-line diagrams, we associate a certain finite number of field lines with a charge of a given magnitude. In the diagrams shown, 8 lines are associated with a charge of magnitude q. Note that field lines of static charge distributions always begin and end on charges, or extend to infinity.

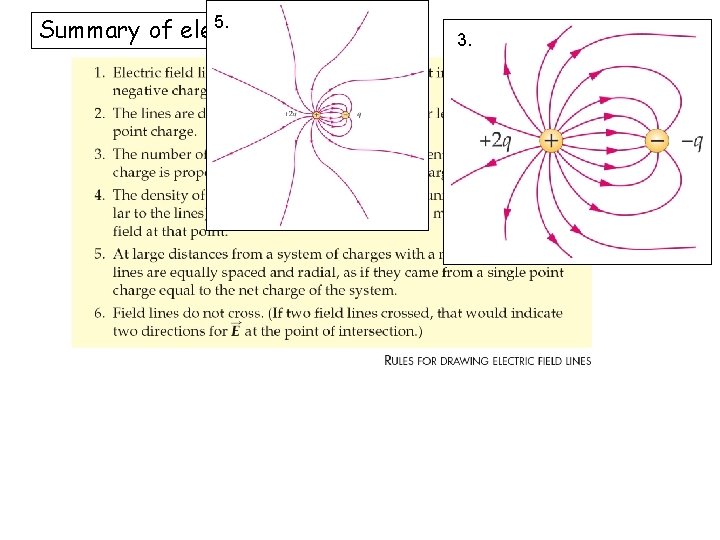
5. Summary of electric field lines 3.

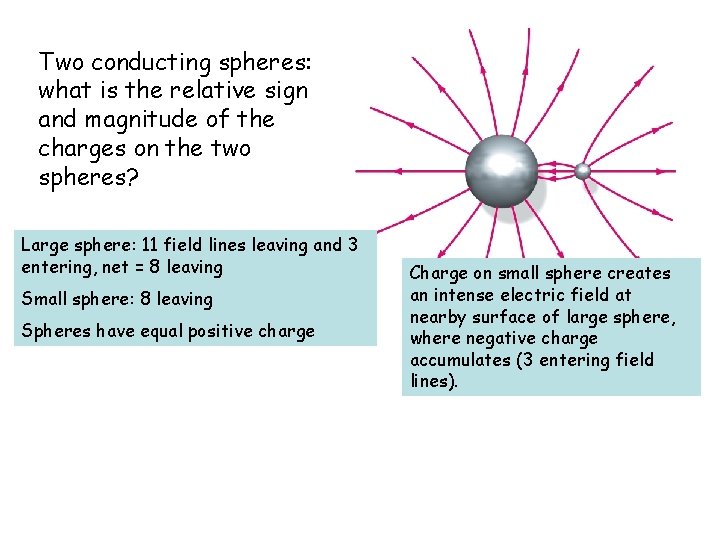
Two conducting spheres: what is the relative sign and magnitude of the charges on the two spheres? Large sphere: 11 field lines leaving and 3 entering, net = 8 leaving Small sphere: 8 leaving Spheres have equal positive charge Charge on small sphere creates an intense electric field at nearby surface of large sphere, where negative charge accumulates (3 entering field lines).

Gauss’s Law A new look at Coulomb’s Law Flux of an Electric Field Gauss’ Law and Coulomb’s Law

A new look at Coulomb’s Law A new formulation of Coulomb’s Law was derived by Gauss (1777 -1855). It can be used to take advantage of symmetry. For electrostatics it is equivalent to Coulomb’s Law. We choose which to use depending on the problem at hand. Two central features are (1) a hypothetical closed surface – a Gaussian surface – usually one that mimics the symmetry of the problem, and (2) flux of a vector field through a surface Gauss’ Law relates the electric fields at points on a (closed) Gaussian surface and the net charge enclosed by that surface

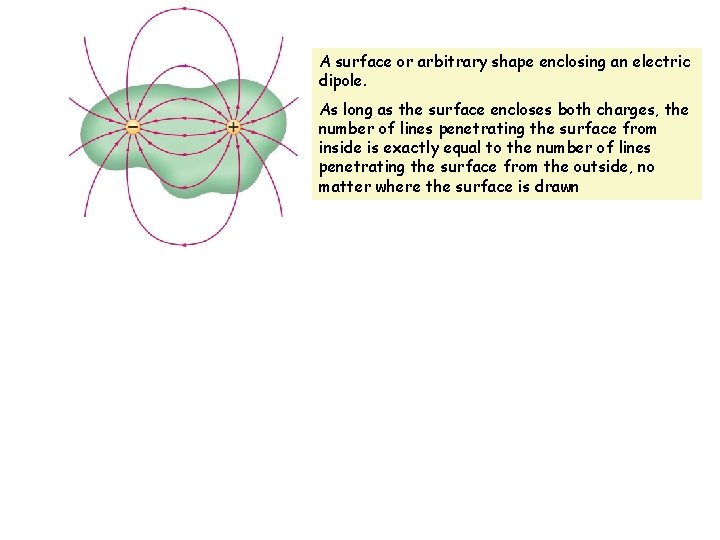
A surface or arbitrary shape enclosing an electric dipole. As long as the surface encloses both charges, the number of lines penetrating the surface from inside is exactly equal to the number of lines penetrating the surface from the outside, no matter where the surface is drawn

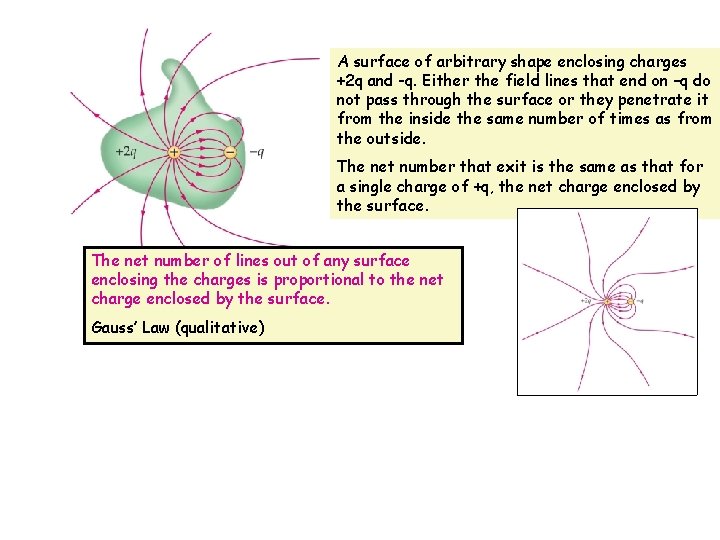
A surface of arbitrary shape enclosing charges +2 q and -q. Either the field lines that end on –q do not pass through the surface or they penetrate it from the inside the same number of times as from the outside. The net number that exit is the same as that for a single charge of +q, the net charge enclosed by the surface. The net number of lines out of any surface enclosing the charges is proportional to the net charge enclosed by the surface. Gauss’ Law (qualitative)

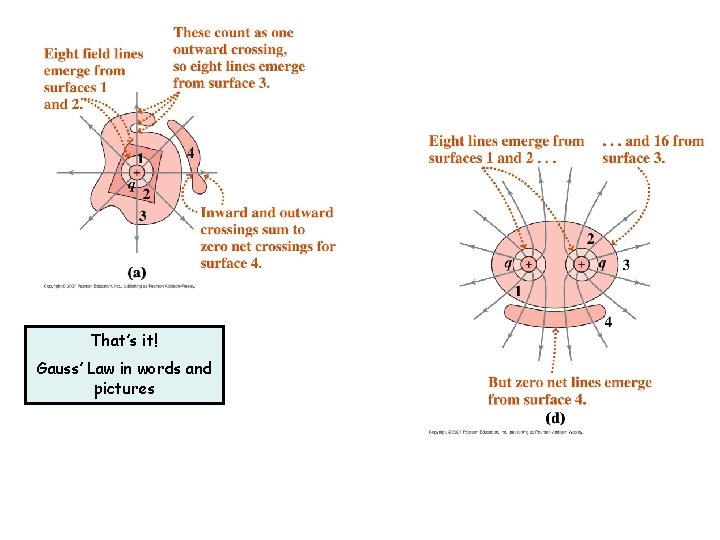
That’s it! Gauss’ Law in words and pictures

21. 2 Electric flux • Electric flux quantifies the notion “number of field lines crossing a surface. ” – The electric flux through a flat surface in a uniform electric field depends on the field strength E, the surface area A, and the angle between the field and the normal to the surface. – Mathematically, the flux is given by • Here is a vector whose magnitude is the surface area A and whose orientation is normal to the surface.

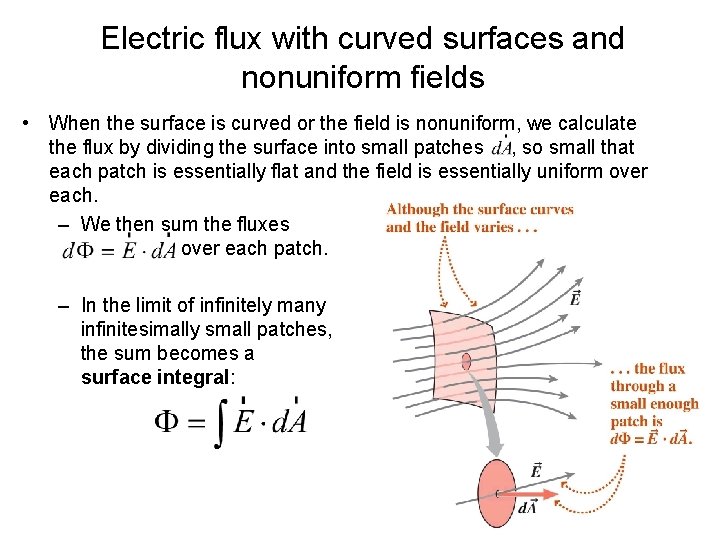
Electric flux with curved surfaces and nonuniform fields • When the surface is curved or the field is nonuniform, we calculate the flux by dividing the surface into small patches , so small that each patch is essentially flat and the field is essentially uniform over each. – We then sum the fluxes over each patch. – In the limit of infinitely many infinitesimally small patches, the sum becomes a surface integral:

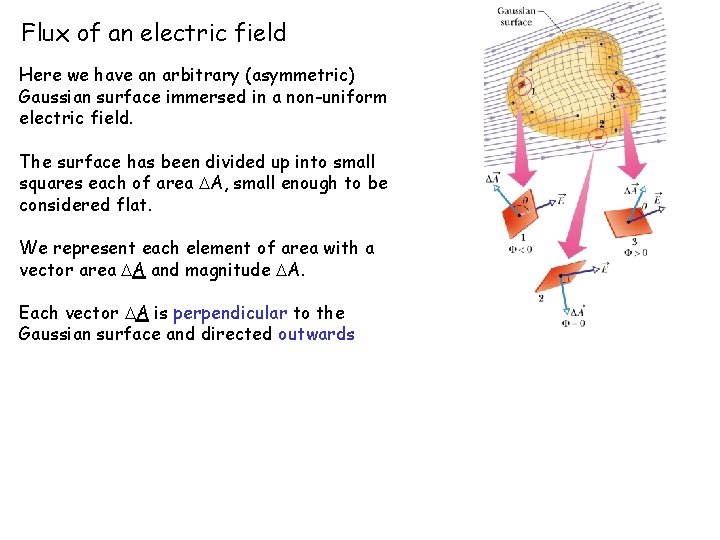
Flux of an electric field Here we have an arbitrary (asymmetric) Gaussian surface immersed in a non-uniform electric field. The surface has been divided up into small squares each of area A, small enough to be considered flat. We represent each element of area with a vector area A and magnitude A. Each vector A is perpendicular to the Gaussian surface and directed outwards

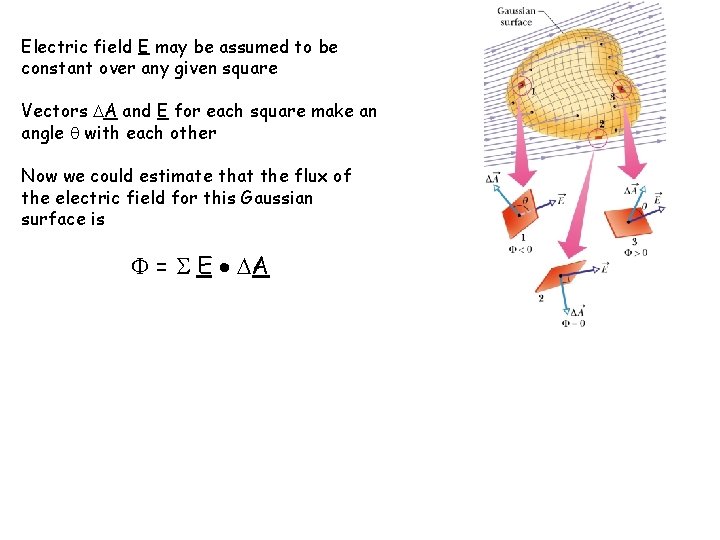
Electric field E may be assumed to be constant over any given square Vectors A and E for each square make an angle with each other Now we could estimate that the flux of the electric field for this Gaussian surface is = E A

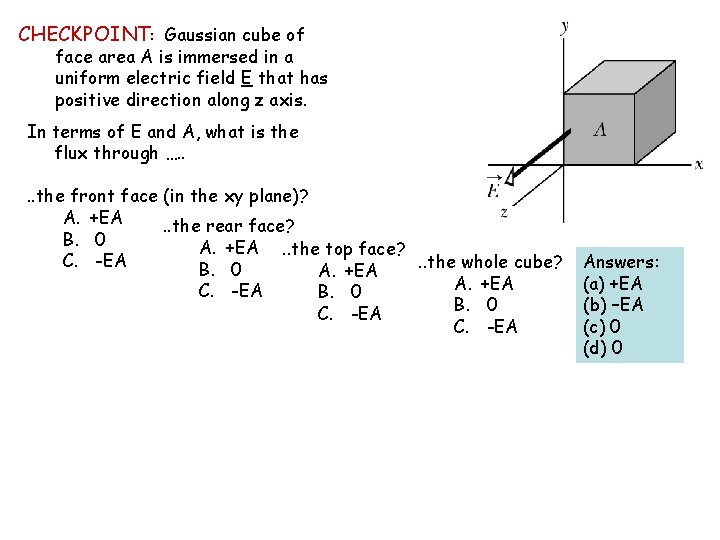
CHECKPOINT: Gaussian cube of face area A is immersed in a uniform electric field E that has positive direction along z axis. In terms of E and A, what is the flux through …. . the front face (in the xy plane)? A. +EA. . the rear face? B. 0 A. +EA. . the top face? C. -EA. . the whole cube? B. 0 A. +EA C. -EA B. 0 C. -EA Answers: (a) +EA (b) –EA (c) 0 (d) 0

The flux through side B of the cube in the figure is the same as the flux through side C. What is a correct expression for the flux through each of these sides? A. B. C. D. End of Lecture 5