Gaussian Process Regression for Dummies Greg Cox Richard

Gaussian Process Regression for Dummies Greg Cox Richard Shiffrin

Continuous response measures

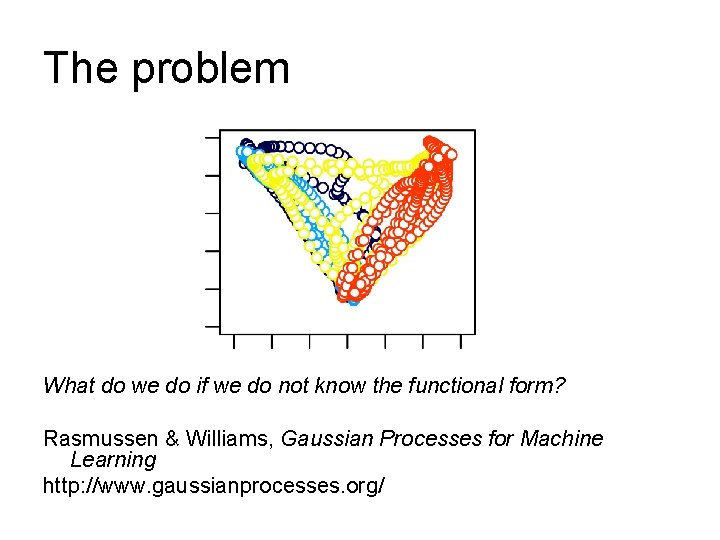
The problem What do we do if we do not know the functional form? Rasmussen & Williams, Gaussian Processes for Machine Learning http: //www. gaussianprocesses. org/

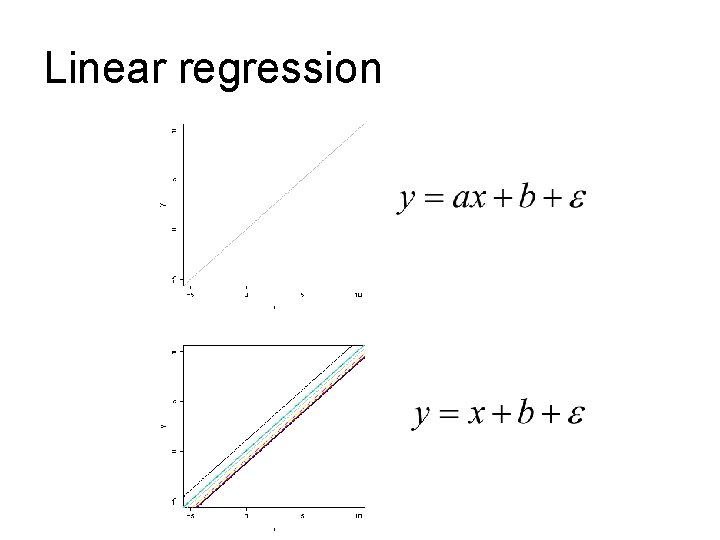
Linear regression

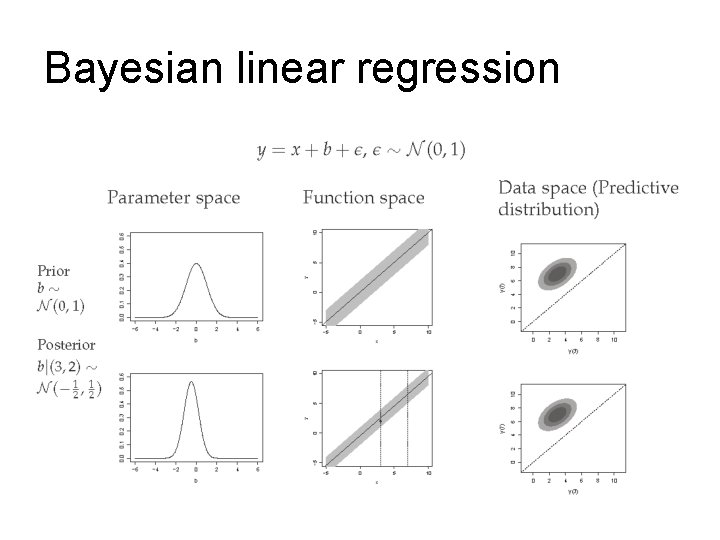
Bayesian linear regression

Gaussian processes A Gaussian process is a collection of random variables, any subset of which is jointly normally distributed. Normal regression: assume functional form mean and covariance among data Gaussian process regression: assume form of mean and covariance among data functional form

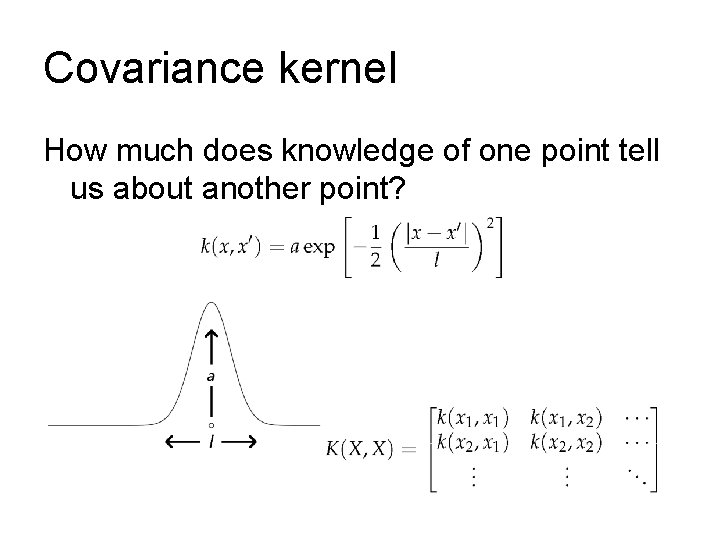
Covariance kernel How much does knowledge of one point tell us about another point?

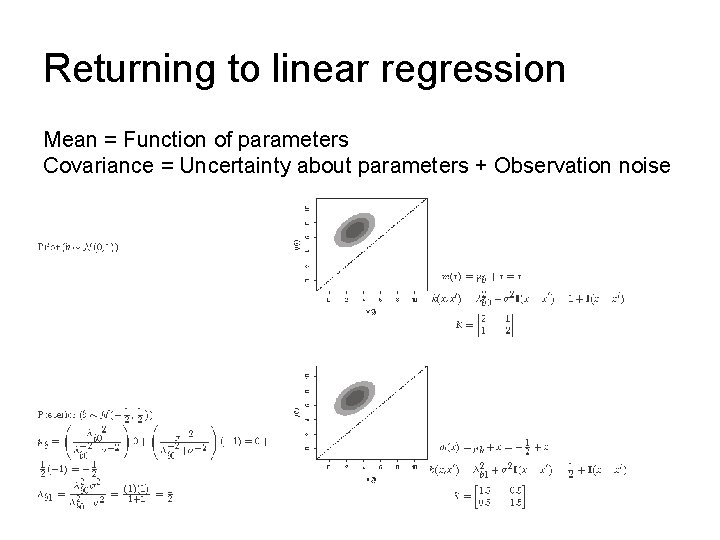
Returning to linear regression Mean = Function of parameters Covariance = Uncertainty about parameters + Observation noise

Takeaways from linear regression • Rather than work in “parameter space”, we can bypass it by just working in “data space” • This allows us to worry only about how different data points relate to one another without needing to specify the parameters of the data generating process • The posterior predictive distribution encapsulates our uncertainty about the data generating process • The choice of covariance kernel—which says how different observations inform one another—implies certain properties of the data generating process

Posterior predictive distribution So far, we have computed the posterior predictive via the parameters (e. g. , b) of the data generating process. But, a Gaussian process may have an infinite number of parameters (q). How can we compute the posterior predictive in this case? The covariance kernel to the rescue! Let’s say we don’t know the data generating process, but we assume all observations are drawn from the same Gaussian process (i. e. , are multivariate normal) and have an idea about how observations can mutually inform one another, the covariance kernel k(x, x’). Then. . . New data values f*(x*), given observed data f(x): But these are all multivariate normal!

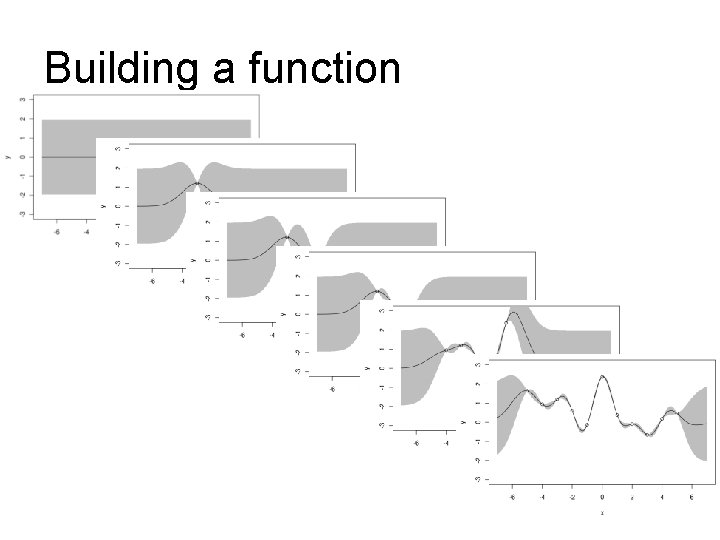
Building a function

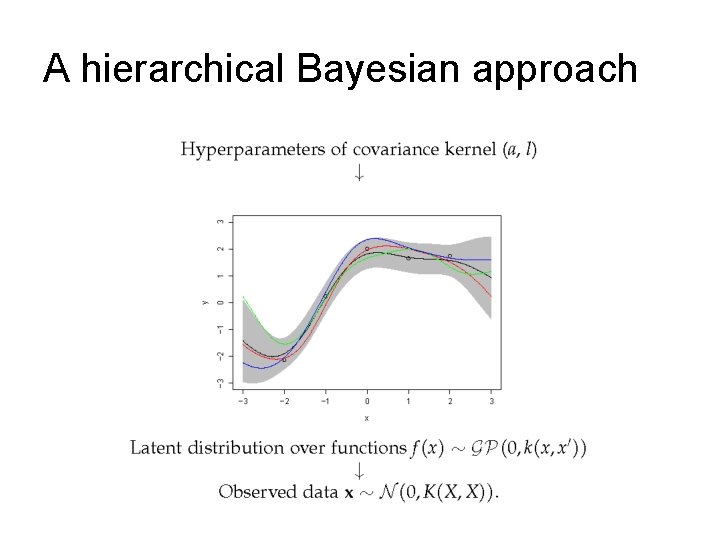
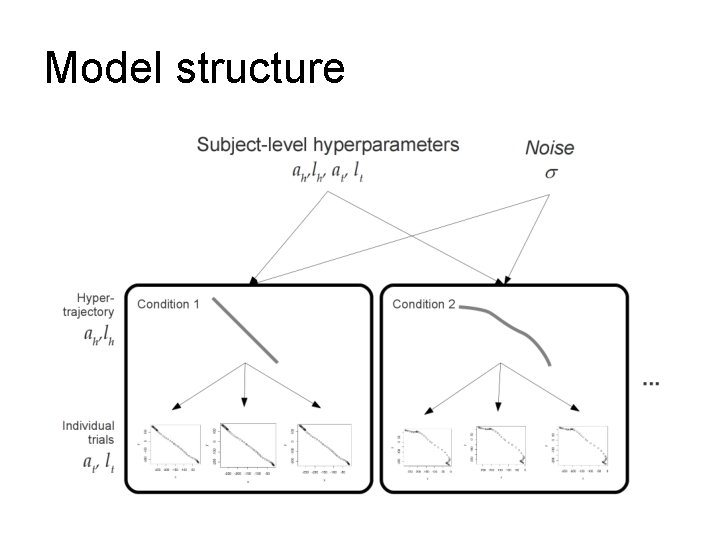
A hierarchical Bayesian approach

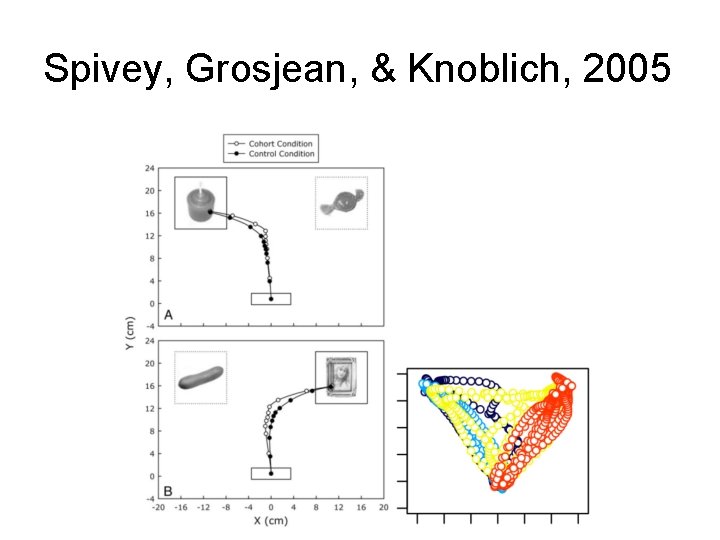
Spivey, Grosjean, & Knoblich, 2005

The GP model

Model structure

The GP model

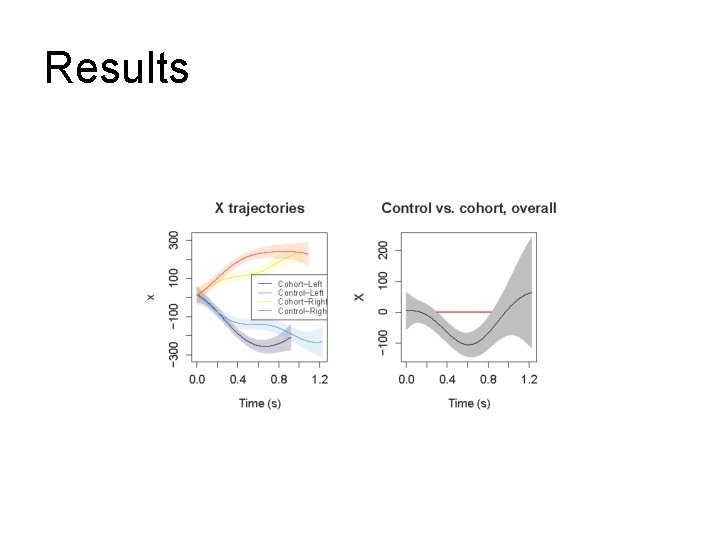
Results

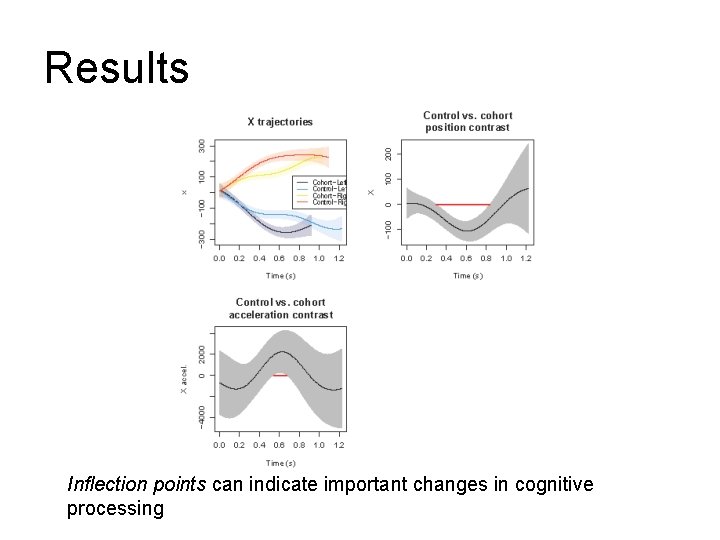
Results Inflection points can indicate important changes in cognitive processing

Summary • Gaussian process models offer a useful and extensible way of dealing with behavioral trajectories • Able to model entire spectrum of dynamics • Can be embedded in a generative model to infer attractors and inflection points • Allow for deeper inferences about underlying cognitive processes