Gaussian Elimination Rank and Cramer We have seen

How Many Solutions Consider these graphs Each graph has 2 lines defined by linear

Matrix Rank The Rank of a Matrix is a property that can be used

Rank by determinants Rank of m*n matrix is largest square submatrix whose det <>

Rank not 3. Is it 2? Try any 2*2 submatrix. Rank = 2 This

Fundamental Theorem of Linear Systems If system defined by m row matrix equation A

Homogeneous Systems If system defined by A x = 0, i. e. b =

Cramer’s Theorem - Solving Equations Suspended Mass Here, D = 0. 96 * 0.

Electronic Circuit Example D = |A| found earlier as – 600 p RJM 15/10/02

Exercise Find A such that Use Cramer’s theorem to find v 2 and i

Slides: 12

Download presentation

Gaussian Elimination, Rank and Cramer We have seen how Gaussian Elimination can solve A x = b But, is it always the case that there is a solution? In fact there may be many solutions…. . we will investigate. This will lead to various topics: Matrix Rank Homogeneous Systems Cramer’s Rule and finally Cramer’s Theorem small matrices) p RJM 15/10/02 – alternative to Gaussian Elimination (for EG 1 C 2 Engineering Maths: Matrix Algebra 6

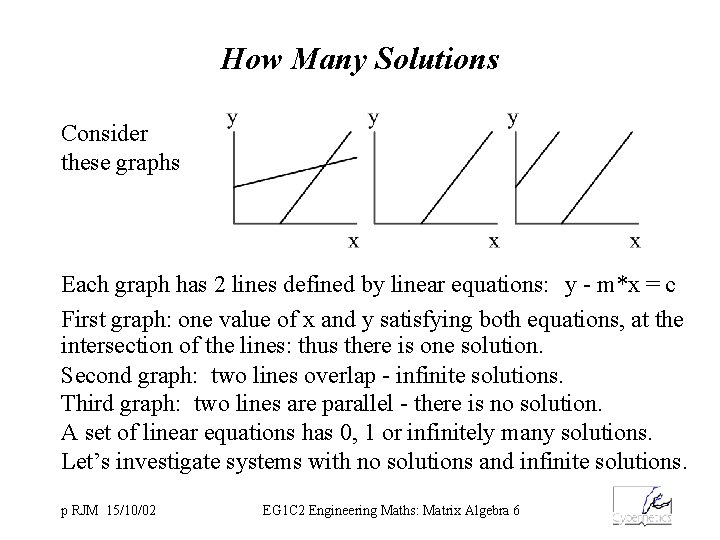
How Many Solutions Consider these graphs Each graph has 2 lines defined by linear equations: y - m*x = c First graph: one value of x and y satisfying both equations, at the intersection of the lines: thus there is one solution. Second graph: two lines overlap - infinite solutions. Third graph: two lines are parallel - there is no solution. A set of linear equations has 0, 1 or infinitely many solutions. Let’s investigate systems with no solutions and infinite solutions. p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

e. g. 2 x + y + 3 z = 4; x + y + 2 z = 0; 2 x + 4 y + 6 z = 8 Eliminating the first column from rows 2 and 3: Row 2 : = Row 1 -2*Row 2 [2 -2*1 1 -2*1 3 -2*2 4 -0] = [0 -1 -1 4] Row 3 : = Row 1 -Row 3 [2 -2 1 -4 3 -6 4 -8] = [0 -3 -3 -4] Row 3 : = 3*Row 2 - Row 3 [0 -3— 3 – 3— 3 12 --4] = [0 0 0 16] Last row means 0 = 16! So, there is no solution. p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

e. g. 2 x + y + 3 z = 4; x + y + 2 z = 0; 2 x + 4 y + 6 z = -8 Eliminating the first element of rows 2 and 3 gives Eliminating the second element of row 3 gives The last row means 0 = 0; True for all values of x, y and z. Thus there is an infinite number of solutions to the 3 equations. In fact the equations are said to be linearly dependent. If there are solutions, the equations are linearly independent. p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

Matrix Rank The Rank of a Matrix is a property that can be used to determine the number of solutions to a matrix equation A x = b. One definition of rank is that it is the number of non zero rows in the augmented matrix when it is in row echelon form. 2 rows are non zero: rank = 2 Here 3 rows are non zero, so rank = 3. But, matrix needed in echelon form first: is there another way? p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

Rank by determinants Rank of m*n matrix is largest square submatrix whose det <> 0. A submatrix of A is a matrix of A minus some rows or columns. Its four 3*3 submatrices are: | a) | is 2*(6 -8) – 1*(6 -4) + 3*(4 -2) = -4 -2+6 = 0 | b) | is 2*(-8 -0) – 1*(-8 -0) + 4*(4 -2) = -16+8+8 = 0 | c) | is 2*(16 -0) – 3*(16 -0) + 4* (6 -2) = 32 – 48 + 16 = 0 | d) | is 1*(-16 -0) – 3*(-8 -0) + 4*(6 -8) = -16 + 24 – 8 = 0 p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

Rank not 3. Is it 2? Try any 2*2 submatrix. Rank = 2 This is the case where there is an infinite number of solutions. Thus Rank ( )=3, but Rank(A) < 3. Here there are no solutions Its rank = 3 This was augmented matrix for circuit which had one solution. Leads to Fundamental Theorem of Linear Systems …. p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

Fundamental Theorem of Linear Systems If system defined by m row matrix equation A x = b The system has solutions only if Rank (A) = Rank ( ) If Rank (A) = m, there is 1 solution If Rank (A) < m, there is an infinite number of solutions Properties of Rank The Rank of A is 0 only if A is the zero matrix. Rank (A) = Rank (AT) Elementary row operations don't affect the rank of a matrix. Rank is a concept quite useful in control theory. This leads to two related and useful topics…… p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

Homogeneous Systems If system defined by A x = 0, i. e. b = 0, system is homogenous. A homogenous system has a trivial solution, x 1=x 2=. . xn=0. A non trivial solution exists if Rank(A) < m. Cramer's Rule For homogeneous systems If D = | A | 0, the only solution is x = 0 If D = 0, the system has ‘non trivial’ solutions, This is useful, as we shall see, for eigenvalues and eigenvectors. Cramer’s Theorem Solutions to a linear system A * x = b , where A is an n*n: x 1 = D 1/D x 2 = D 2/D. . xn = Dn/D where D is det|A| , D <> 0, and Dk is det of matrix formed by taking A and replacing its kth column with b. Impracticable in large matrices as hard to find their determinant. p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

Cramer’s Theorem - Solving Equations Suspended Mass Here, D = 0. 96 * 0. 6 - -0. 8 * 0. 28 = 0. 8 Replacing first column of A with b and taking determinant: Thus T 1 = 240 / 0. 8 = 300 Replacing second column of A with b and taking determinant: Thus T 2 = 288 / 0. 8 = 360 These agree with earlier results. Good! p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

Electronic Circuit Example D = |A| found earlier as – 600 p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6

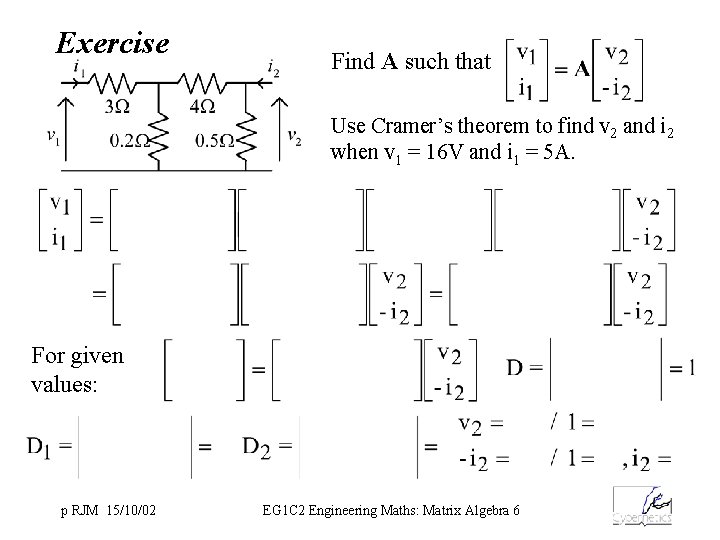
Exercise Find A such that Use Cramer’s theorem to find v 2 and i 2 when v 1 = 16 V and i 1 = 5 A. For given values: p RJM 15/10/02 EG 1 C 2 Engineering Maths: Matrix Algebra 6