GAUSS ELIMINATION BACK SUBSTITUTION Dayun Yu Seungmuk Ji

GAUSS ELIMINATION & BACK SUBSTITUTION Dayun Yu Seungmuk Ji SNPL 1

Gauss Elimination n n matrix : A , n-vector : x and b, Ax = b The solution vector x can be obtained without difficulty in case A is upper-triangular with all diagonal. Ax = b SNPL 2

Back Substitution ann 0, We must have We now know xn, the second last equation Similarly, In general SNPL 3
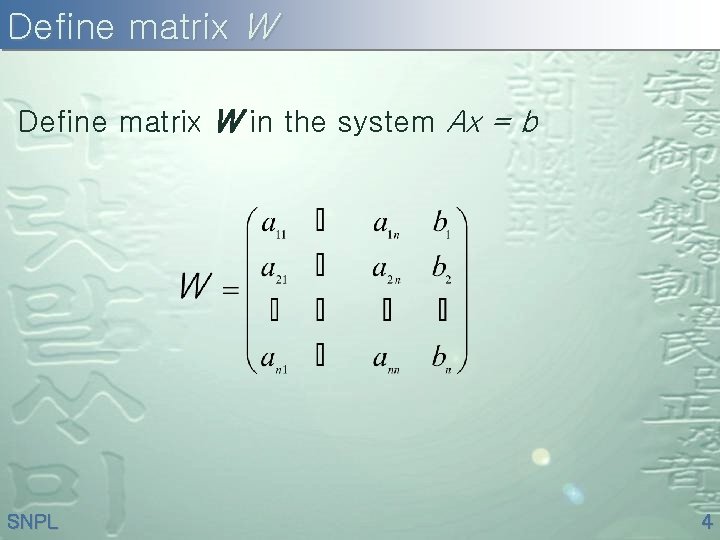
Define matrix W in the system Ax = b SNPL 4

Pivoting Partial-pivoting is interchanging row. ☞ If first column(a 11=0) of first row is zero, we have to interchange other row. Full-pivoting is interchanging row and columns. ☞ If is satisfy, we must find . So we execute interchanging row ( row i row p). SNPL 5

Example Ex) SNPL 6

Algorithm 1 (Upper-triangular) Initialize the n-vector p to have pi = i, i = 1, , n. For k = 1, ∙∙∙, n-1, do; For i = k+1, ∙∙∙, n , do; set m and , m equal to . For j = k+1, ∙∙∙, n+1, do; set. SNPL 7

Algorithm 2 (Back substitution) For k = n, n-1, ∙∙∙, 1 , do; calculate SNPL . 8

Programming with C #include <stdio. h> #include <math. h> #include <conio. h> main() { int i, j, k, t; int n, N; float m, s; float w[3][4]={{2, 3, -1, 5}, {4, 4, -3, 3}, {-2, 3, -1, 1}}; float p[3]={0. 0}; clrscr(); n = 3; N = 4; printf("nn***** Matrix W ****nn"); for(i = 0; i < n; i++) { for(j = 0; j < N; j++) printf("%10. 3 f", w[i][j]); printf("n"); p[i] = i; } SNPL for(k = 0; k < n-1; k ++) { for(j = k; j < N; j++) { if(j == n) { printf(" W is not invertible ! "); break; } else if(w[p[j]][k] == 0) continue; else { for(t = k; t < N; t++) { s = w[p[j]][t]; w[p[j]][t] = w[p[k]][t]; w[p[k]][t] = s; } } break; } for(i = k+1; i < n; i++) { q = w[p[i]][k] / w[p[k]][k]; for(j = k; j < N; j++) w[p[i]][j] = w[p[i]][j] - q*w[p[k]][j]; } } 9

Programming with C printf("nn"); for(i = 0; i < n; i++) { for(j =0; j < N; j++) printf("%10. 3 f", w[p[i]][j]); printf("n"); } } getch(); return(0); } SNPL 10

Result ***** Matrix W **** 2. 000 4. 000 -2. 000 3. 000 -1. 000 4. 000 -3. 000 -1. 000 2. 000 0. 000 3. 000 -1. 000 5. 000 -2. 000 -1. 000 -7. 000 0. 000 -5. 000 -15. 000 SNPL 5. 000 3. 000 11

General program with C #include <stdio. h> #include <conio. h> #include <math. h> #include <stdlib. h> #define MAXROW 20 gainp(a, b); gacal(a, b); getch(); return 0; } typedef struct { int Row, Column; double Element[MAXROW][MAXROW+1]; } Matrix; void gainp(int a, int b) { int i, j; double tmp; printf(“n”); printf("Enter the matrix (%2 d, %2 d) n", a, b); for(i=0; i<a; i++) { for(j=0; j<b; j++){ printf("Enter for element (%2 d, %2 d) : ", i+1, j+1); scanf(" %lf", &tmp); M. Element[i][j]=tmp; } printf("n"); } } Matrix M; void gainp(int a, int b); void gapiv(int row, int i); void gacal(int row, int col); int main() { int a, b; clrscr(); printf(“Row is : ”); scanf(“%2 d”, &a); printf(“Column is : ”); scanf(“%2 d”, &b); SNPL 12

General program with C void gapiv(int row, int i) { int j, ii; double tmp; for(ii=i+1; ii<row; ii++){ if(M. Element[ii][i]!=0. 0){ for(j=i; j<row+1; j++){ tmp=M. Element[i][j]; M. Element[i][j]=M. Element[ii][j]; M. Element[ii][j]=tmp; } break; } } } void gacal(int row, int col) { int i, j, k, N; double div, sum, X[MAXROW]; for(i=0; i<row; i++){ if(M. Element[i][i]==0. 0) gapiv(row, i); SNPL for(j=i+1; j<row; j++){ div=M. Element[j][i]/M. Element[i][i]; for(k=0; k<col; k++) M. Element[j][k]-=M. Element[i][k]*div; } } N=row; X[N-1]=M. Element[N-1][N]/M. Element[N-1]; for(i=N-2; i>=0; i--){ sum=0. 0; for(j=i+1; j<N; j++) sum += M. Element[i][j]*X[j]; X[i]=(M. Element[i][N]-sum)/M. Element[i][i]; } printf("Solution is : n"); for(i=0; i<N; i++) printf(" X%-d = %fn", i+1, X[i]); } 13
- Slides: 13