Gauss divergensteorem Alternative former Archimedes lov Gauss Divergensteorem

Gauss’ divergensteorem Alternative former Archimedes lov

Gauss’ Divergensteorem Alternative former - Oppsummering

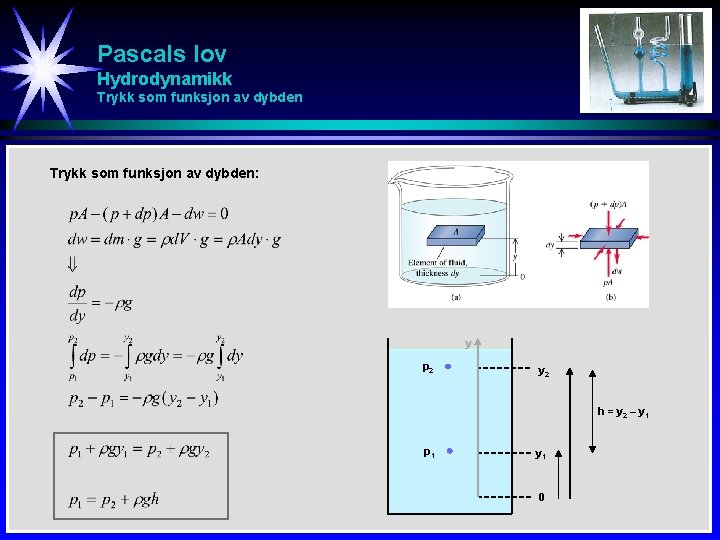
Pascals lov Hydrodynamikk Trykk som funksjon av dybden: y p 2 y 2 h = y 2 – y 1 p 1 y 1 0

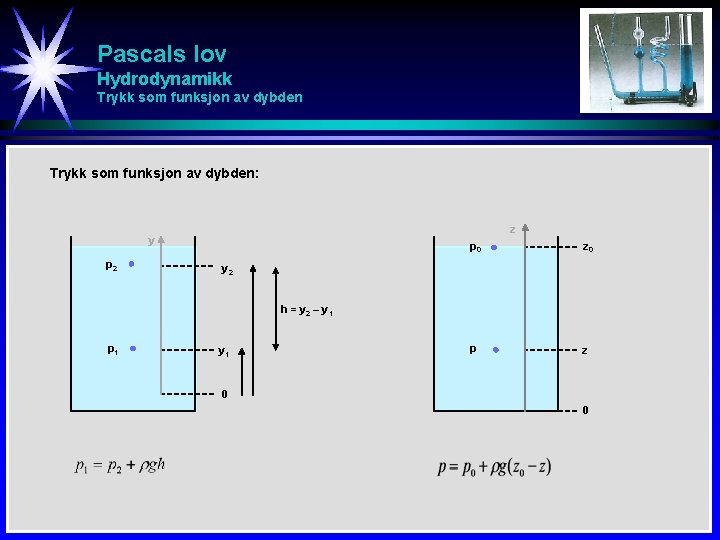
Pascals lov Hydrodynamikk Trykk som funksjon av dybden: z y p 2 p 0 z 0 p z y 2 h = y 2 – y 1 p 1 y 1 0 0

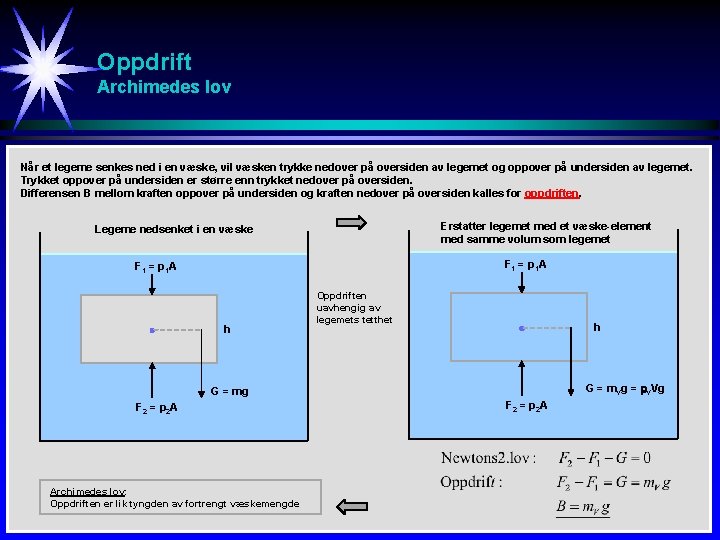
Oppdrift Archimedes lov Når et legeme senkes ned i en væske, vil væsken trykke nedover på oversiden av legemet og oppover på undersiden av legemet. Trykket oppover på undersiden er større enn trykket nedover på oversiden. Differensen B mellom kraften oppover på undersiden og kraften nedover på oversiden kalles for oppdriften. Erstatter legemet med et væske-element med samme volum som legemet Legeme nedsenket i en væske F 1 = p 1 A h Oppdriften uavhengig av legemets tetthet h G = m. Vg = VVg G = mg F 2 = p 2 A Archimedes lov: Oppdriften er lik tyngden av fortrengt væskemengde F 2 = p 2 A

Del-operator Hydrodynamikk - Archimedes’ lov: Når et legeme senkes ned i en væske, vil oppdriften som virker på legemet (kraften fra væsken på legemet) være lik tyngden av fortrengt væskemengde. Vi tenker oss et kar med væske. Vi plasserer en z-akse vertikalt oppover med origo i bunnen av karet. La p 0 være trykket på toppen av væsken, dvs p 0 er lik lufttrykket over væsken. og la z 0 være posisjonen (høyden til toppen av væsken), dvs høyden opp til væskeoverflaten. z Trykket p i en høyde z i væsken er da gitt ved: p 0 z 0 p z hvor er tettheten av væsken ( betraktes som konstant i hele væsken) og g er tyngdeakselerasjonen. a) Bestem gradienten til den skalare funksjonen p. b) Benytt Gauss’ divergensteorem til å bestemme Archimedes’ lov. 0

Del-operator Hydrodynamikk - Archimedes’ lov a) Gradienten til trykket p:

Del-operator Hydrodynamikk - Archimedes’ lov b) Archimedes’ lov: Vi lar n 1 -vektor være enhetsnormalvektor inn mot en infinitesimal flate d. S av legemet. Kraften fra væsken inn mot denne infinitesimale flaten vil da ha en størrelse pd. S og ha retning langs n 1 -vektor. La n-vektor være enhetsnormalvektoren på den infinitesimale flaten d. S med retning ut fra flaten d. S. n-vektor er da den vektoren som inngår i Gauss’ teorem (både original og alternativ form). Oppdriften B-vektor vil nå være lik vektorsummen av alle slike infinitesimale krefter (med størrelse pd. S og retning normalt inn mot legemet), dvs dobbeltintegrlatet over hele overflaten av legemet av pd. S multiplisert med n 1 -vektor. Til beregning av dette dobbeltintegralet benytter vi den nevnte alternative formen av Gauss’ teorem. B n

END