GASES Unit 2 Ch 4 Pg 146 180

GASES ¬ ¬ ¬ Unit 2 Ch. 4 Pg. 146 -180

Chapter 4 Gases and the Kinetic Molecular Theory A. Properties of Gases ¬we use many technologies that were designed with the knowledge of the properties of gases eg) SCUBA equipment, hot air balloons, jackhammers

¬gases have several distinct macroscopic (visible) properties: Ø gases are compressible ie) pressure = volume Ø gases expand as temperature increases ie) temperature = volume (not confined) temperature = pressure (confined) Ø gases have low resistance to flow (viscosity) …allows them to escape quickly through small openings

Ø gases have low densities Ø gases mix evenly and completely, they all are miscible Ø gases have no shape or volume, they fill the shape of the container they are in

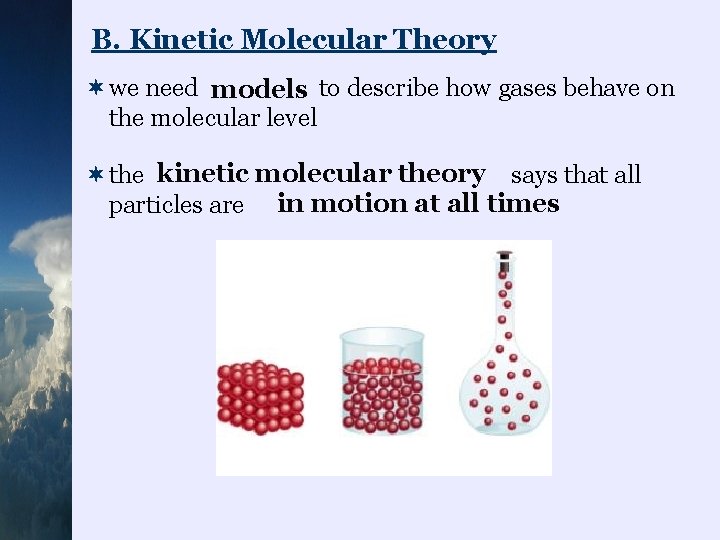
B. Kinetic Molecular Theory ¬we need models to describe how gases behave on the molecular level ¬the kinetic molecular theory says that all particles are in motion at all times

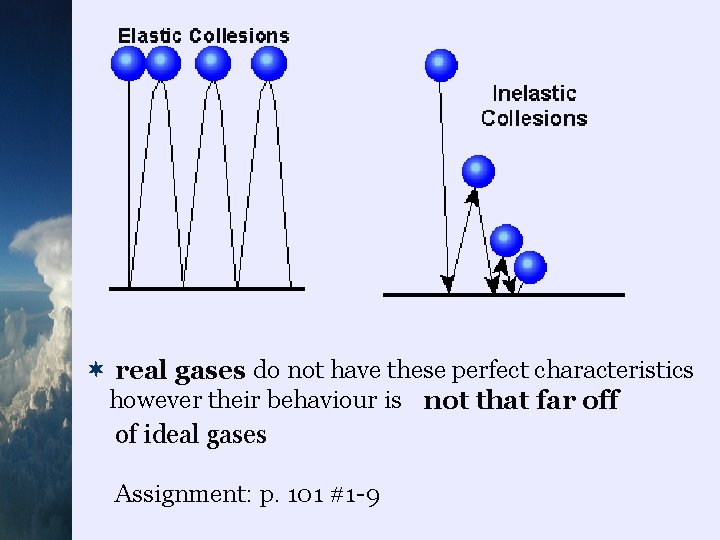
¬an ideal gas (which is hypothetical) is defined by the following characteristics: 1. the gas molecules are in constant random motion where they move in a straight line until they collide with a particle or wall of the container 2. the gas molecules are “point masses” (they have mass but no volume ) 3. the only interaction between molecules of the gas and container are elastic collisions… collisions where kinetic energy is conserved

¬ real gases do not have these perfect characteristics however their behaviour is not that far off of ideal gases Assignment: p. 101 #1 -9

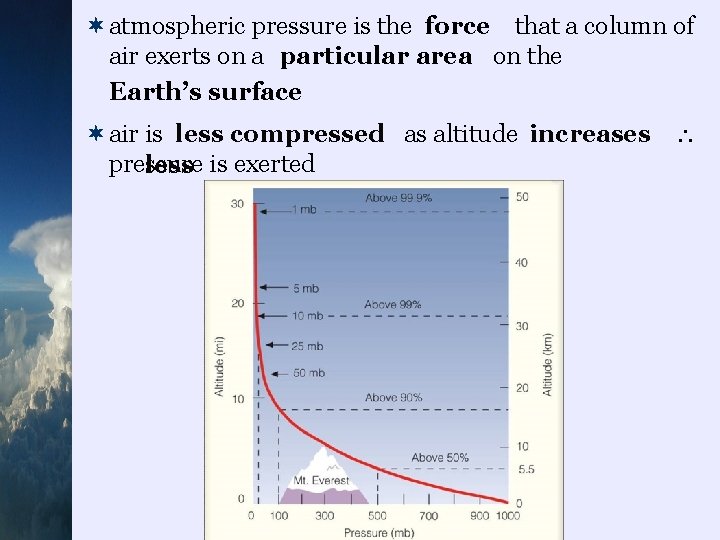
3. 2 Gases and Pressure A. Atmospheric Pressure ¬although gas molecules have very little mass , the Earth’s gravitational pull keeps them near the surface of the planet which creates our atmosphere ¬ pressure = force per unit area ¬pressure is exerted in all directions to the same extent

¬atmospheric pressure is the force that a column of air exerts on a particular area on the Earth’s surface ¬air is less compressed as altitude increases pressure less is exerted

B. Measuring Pressure ¬Pascal and Perier used Hg(l)to prove that atmospheric pressure decreases with altitude ¬the work of Pascal, Perier and Torricelli all led to the development of the mercury barometer

¬there are several different units used to measure pressure: Ø millimetres of mercury (mm. Hg) Øthe Pascal (Pa) Øthe kilopascal (k. Pa) Øthe atmosphere (atm) Øthe bar

¬you will be using the standard unit of k. Pa in gas law calculations and therefore you must be able to convert mm. Hg and atm to k. Pa ¬memorize the following standard atmospheric pressures: 760 mm. Hg = 1 atm = 101. 325 k. Pa ¬another conversion: 1 bar = 100 k. Pa ¬to convert other units of pressure to k. Pa, set up a ratio

Example 1 Convert 650 mm. Hg to k. Pa. 101. 325 k. Pa 760 mm. Hg = x 650 mm. Hg x = 86. 6… k. Pa

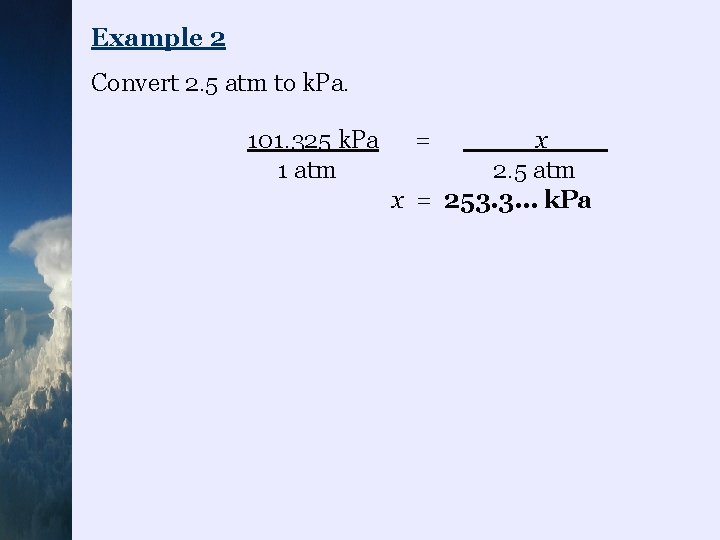
Example 2 Convert 2. 5 atm to k. Pa. 101. 325 k. Pa 1 atm = x 2. 5 atm x = 253. 3… k. Pa

Try These: Convert the following pressures to k. Pa (unrounded): 1. 4. 0 atm 405. 3 k. Pa 2. 855 mm. Hg 113. 9…k. Pa 3. 0. 625 atm 63. 3…k. Pa 4. 150 mm. Hg 19. 9…k. Pa

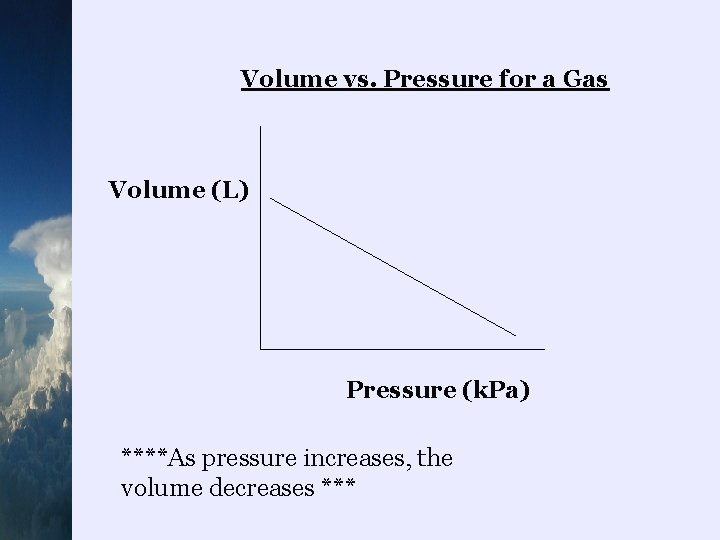
Boyle’s Law ¬Irish scientist Robert Boyle studied the relationship between the pressure and volume of gases at constant temperatures ¬pressure on the walls of a container is caused by the collisions of the gas molecules with the walls ¬as you reduce the volume of a contained gas, there is less room for the gas particles so they collide more ¬ more collisions = higher pressure http: //michele. usc. edu/java/gassim. html

Volume vs. Pressure for a Gas Volume (L) Pressure (k. Pa) ****As pressure increases, the volume decreases ***

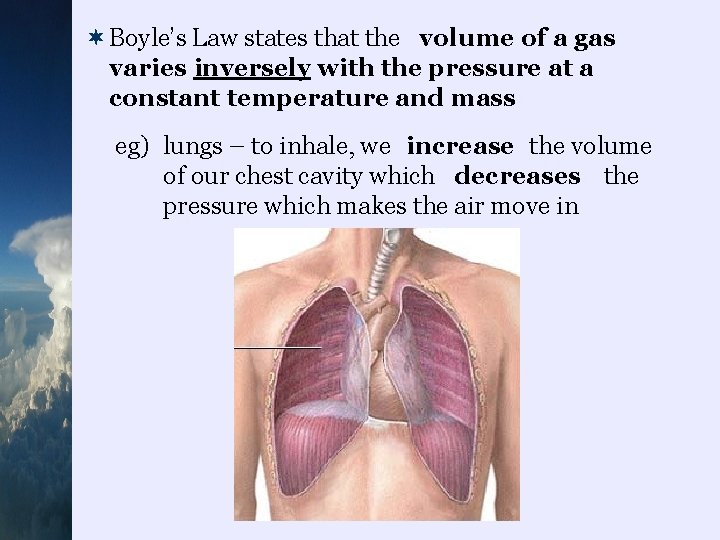
¬Boyle’s Law states that the volume of a gas varies inversely with the pressure at a constant temperature and mass eg) lungs – to inhale, we increase the volume of our chest cavity which decreases the pressure which makes the air move in

eg) breath-hold diving – all air containing spaces in body shrink as pressure increases with depth…this doesn’t happen with SCUBA gear

P 1 V 1 = P 2 V 2 where: P 1, P 2 = pressures in k. Pa V 1, V 2 = volumes in L

Example 1 A balloon is filled with 30. 0 L of helium gas at 100 k. Pa. What is the volume when the balloon rises to an altitude where the pressure is only 25. 0 k. Pa? (assume constant temperature) P 1 = 100 k. Pa P 2 = 25. 0 k. Pa V 1 = 30. 0 L P 1 V 1 = P 2 V 2 (100 k. Pa)(30. 0 L) = (25. 0 k. Pa) V 2 = 120 L

Example 2 The pressure on 2. 50 L of anesthetic gas is 100 k. Pa. If 6. 25 L of gas is the required volume, what pressure must it be under assuming constant temperature? P 1 = 100 k. Pa V 1 = 2. 50 L V 2 = 6. 25 L P 1 V 1 = P 2 V 2 (100 k. Pa)(2. 50 L) = P 2 (6. 25 L) P 2 = 40. 0 k. Pa

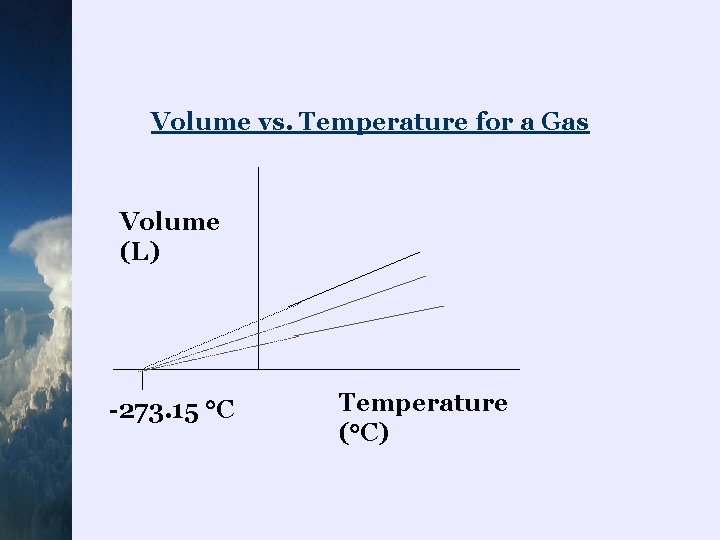
Volume vs. Temperature ¬when volume vs. temperature of a gas are graphed, the plot is linear (as long as amount of gas and pressure were constant) ¬it was also noticed that when these linear plots were extrapolated down to zero volume, all the lines converged at one point

Volume vs. Temperature for a Gas Volume (L) -273. 15 C Temperature ( C)

¬the temperature when the volume of a gas is zero is 273. 15 C ¬ Lord Kelvin , in 1848, suggested that this is the lowest possible temperature or absolute zero ¬he established a new temperature scale which is called the Kelvin scale in his honour

¬ t is used for temperature in C ¬ T is used for temperature in K ¬ -273. 15 C = absolute zero = zero Kelvin ¬to go from C to K… you add 273. 15 eg) 0 C = 273. 15 K 25 C = 298. 15 K -30 C = 243. 15 K -273. 15 C = 0 K

Charles’ Law ¬ Jacques Charles (and Joseph Louis Gay-Lussac) noticed that there was a relationship between the temperature and volume of a gas ¬as temperature increases , so does the kinetic energy of the gas molecules ¬as the molecules move faster , they exert higher pressure ¬the volume of the gas will expand under this pressure until it reaches atmospheric pressure

¬Charles’ Law states that the volume of a gas varies directly with the temperature at a constant pressure and mass V 1 = V 2 T 1 T 2 where: T 1, T 2 = temperatures in K V 1, V 2 = volumes in L

Example 1 A balloon was inflated at 27 C and has a volume of 4. 0 L. If it is heated to 57 C, what is the new volume? (assume constant pressure) T 1 = 27 C = 300. 15 K V 1 = 4. 0 L T 2 = 57 C = 330. 15 K V 1 = V 2 T 1 T 2 (4. 0 L) = V 2 (300. 15 K) 330. 15 K V 2 = 4. 39… L V 2 = 4. 4 L

Example 2 A sample of gas occupies 6. 8 L at 110 C. What will the final temperature be in C when the volume is decreased to 5. 6 L? T 1 = 110 C = 383. 15 K V 1 = V 2 V 1 = 6. 8 L T 1 T 2 V 2 = 5. 6 L (6. 8 L) = 5. 6 L (383. 15 K) T 2 = 315. 5… K – 273. 15 T 2 = 42 C

Remember when doing formulas ¬ ¬ ¬ Volume is in liters- so if m. L convert to L Pressure is in k. Pa so if in atm or mm. Hg convert Temperature is in K- so if in °C convert to K ***for pressure questionconversions wont change your answer BUT it is good practice as upcoming formulas it will matter a LOT Include units (L, k. Pa, K etc) Answers in sig digs

Chapter 4 - pg. 156 Combined Gas Law Calculations ¬ STP = standard temperature and pressure = 273. 15 K (0 C) and 101. 325 k. Pa ¬ SATP = standard ambient temperature and pressure = 298. 15 K (25 C) and 100. 000 k. Pa ¬now we’ll combine Boyle’s Law and Charles’ Law P 1 V 1 = P 2 V 2 T 1 T 2 where: V 1, V 2 = volumes in L T 1, T 2 = temperatures in K P 1, P 2 = pressures in k. Pa

Example 1 A weather balloon is filled with H 2(g) at 20 C and 100 k. Pa. It has a volume of 7. 50 L. It rises to an altitude where the air temperature is -36 C and the pressure is 28 k. Pa. What is the new volume of the balloon? T 1 = 20 C = 293. 15 K V 1 = 7. 50 L P 1 = 100 k. Pa P 2 = 28 k. Pa T 2 = -36 C = 237. 15 K P 1 V 1 = P 2 V 2 T 1 T 2 (100 k. Pa)(7. 50 L) = (28 k. Pa)V 2 (293. 15 K) (237. 15 K) V 2 = 21. 6…L V 2 = 22 L

Example 2 A large syringe was filled with 50. 0 m. L of ammonia gas at STP. If the gas was compressed to 25. 0 m. L with a pressure of 210 k. Pa, what was the final temperature in C? T 1 = 0 C = 273. 15 K V 1 = 0. 0500 L P 1 = 101. 325 k. Pa P 2 = 210 k. Pa P 1 V 1 = P 2 V 2 = 0. 0250 L T 1 T 2 (101. 325 k. Pa)(0. 0500 L) = (210 k. Pa)(0. 0250 L) (273. 15 K) T 2 = 283. 0…K – 273. 15 T 2 = 9. 91 C

Your Assignment ¬ ¬ ¬ Practice questions Read pg. 148 -158 Small quiz tomorrow n n n Memorization 1 question of each law Multiple choice theory

B. Combining Volumes of Gases ¬ Gay-Lussac analyzed chemical reactions that involved gases ¬he studied the volumes of the gaseous reactants and products and concluded that the gases combine in very simple proportions

¬the Law of Combining Volumes states that, when gases react, the volumes of the gaseous reactants and products, measured at constant temperature and pressure, are always in whole number ratios eg) 1 N 2(g) + 3 H 2(g) 2 NH 3(g) 1 : 3 : 2 is the volume ratio For every one mole of nitrogen gas and three moles of hydrogen gas, 2 moles of ammonia gas is produced Formula: v 1 = v 2 n 1 = n 2 Balancing coefficients

Avogadro connection ¬ After Gay-Lussac published his work Avogadro developed another theory called: Avogadro’s theory which states: equal volumes of gases at the same temperature & presssure contain equal numbers of moles. ¬ This theory supports Lussac’s gas law. For example, if a reaction occurs between 1 volume of a gas and three volumes of another gas at the same temperature and pressure, theory says that one molecule of the first gas reacts with three molecules of the second gas.

Example What volume of nitrogen is used up if 100 m. L of ammonia is formed in a composition reaction? (Compare ratios of volume: coefficients for what values you know, and what values you are solving for) N 2(g) + 3 H 2(g) x m. L 2 NH 3(g) 100 m. L Formula: v 1 = v 2 n 1 = n 2 x m. L = 100 m. L 1 = 2 x m. L = 50. 0 m. L

Molar Volume of Gases- pg. 169 ¬ ¬ Molar volume is the volume that one mole of a gas occupies at a specified temperature and pressure. Usually use either STP or SATP for experiments SATP molar volume= 24. 8 L/mol STP molar volume= 22. 4 L/mol

Molar Volume ¬ ¬ ¬ Can be used as a conversion factor to convert chemical amount to volume Formula: V= n x Vm Where: V= volume (L) n= moles (mol) Vm = molar volume (L/mol)

¬ ¬ ¬ Sometimes… You may be given the mass (m) of a substance in your question and will need to first determine the moles Formula: M=m/n Where: M= molar mass (g/mol) m=mass (g) n= moles (mol)

Example #1 ¬ Calculate the volume by 0. 024 mol of carbon dioxide at SATP

Example #2 ¬ Calculate the volume of 6. 2 g of hydrogen gas at STP

Ideal Gas Law ¬ ¬ ¬ An ideal gas is a hypothetical gas that obeys all the gas laws perfectly under all conditions; that is, it does not condense into a liquid when cooled, and graphs of V vs. T are perfectly straight lines Ideal gases are non-existent but we use them as a reference to guide our understanding of real gases The kinetic molecular theory provides a good explanation of gas pressure, temperature, and the gas laws for an ideal gas We can use this explanation to develop interpretations of real gases

KMT assumption for ideal gases Gas molecules are far apart Molecule size is negligible Gas molecules are in constant, random straight line motion (translational) Gas molecules undergo perfect collisions in which no energy is lost; rebound occurs very quickly

Interpretation of real gases For high pressures the molecules are forced close together and the gas is more dense, therefore, the molecule size becomes significant As temperature decreases molecules slow down At some point the intermolecular attractions cause molecules to stick together becoming a liquid Real gas molecules are more like ‘ soft ’ spheres causing longer rebound during collision

¬ There is considerable experimental evidence to suggest that, for relatively low pressures and high temperatures such as STP and SATP conditions, real gases behave very nearly like ideal gases ¬ In this course, all gases are dealt with as if they are ideal in order to simplify our understanding and work with mathematical equations.

¬ ¬ An ideal gas equation describes the interrelationship of pressure, temperature, volume, and chemical amount of matter- the four variables that define a gaseous system. It is derived from the following relationship: n. V = (a constant) × 1/P × T × n

Ideal Gas Law A. Ideal Gas Law Calculations ¬this law combines all four variables (P, V, n and T) into one equation: PV = n. RT where: V = volume in L T = temperature in K P = pressure in k. Pa n = number of moles in mol R = universal gas constant = 8. 314 k. Pa L/mol K

Example 1 What is the volume of 10. 8 mol of oxygen gas at 100. 00 k. Pa and 15. 5 C? n = 10. 8 mol T = 15. 5 C = 288. 65 K P = 100. 00 k. Pa R = 8. 314 k. Pa L/mol K PV = n. RT (100. 00 k. Pa)V = (10. 8 mol)(8. 314 k. Pa L/mol K)(288. 65 K) V = 259. 1…L = 259 L

Example 2 A rigid steel vessel with a volume of 20. 0 L is filled with nitrogen gas to a pressure of 20 000 k. Pa at 27. 0 C. What is the number of moles of nitrogen? T = 27 C = 300. 15 K V = 20. 0 L P = 20 000 k. Pa R = 8. 314 k. Pa L/mol K PV = n. RT (20 000 k. Pa)(20. 0 L) = n(8. 314 k. Pa L/mol K)(300. 15 K) n = 160. 2…mol = 160 mol

Example 3 What is the pressure exerted by 15. 5 g of methane, CH 4(g), if it occupies a volume of 10. 0 L at 25 C? T = 25 C = 298. 15 K V = 10. 0 L R = 8. 314 k. Pa L/mol K m = 15. 5 g M = 16. 05 g/mol n=m M = 15. 5 g 16. 05 g/mol = 0. 965…mol PV = n. RT P(10. 0 L) = (0. 965…mol)(8. 314 k. Pa L/mol K)(298. 15 K) P = 239. 3…k. Pa = 2. 4 102 k. Pa OR PV = m. RT M

Example 4 What is the mass of hydrogen gas contained in a 4. 5 L weather balloon at 25 C and 102. 0 k. Pa? T = 25 C = 248. 15 K V = 4. 5 L P = 102. 0 k. Pa R = 8. 314 k. Pa L/mol K M = 2. 02 g/mol PV = m. RT M (102. 0 k. Pa)(4. 5 L) =m(8. 314 k. Pa L/mol K)(248. 15 K) 2. 02 g/mol (102. 0)(4. 5)= m(1021. 346…. ) (102. 0)(4. 5) = m (1021. 346. . ) = 0. 449…g = 0. 45 g

B. Dalton’s Law of Partial Pressures ¬Dalton’s law of partial pressures states that in a mixture of gases that do not react chemically, the sum of the partial is thetotal pressures of each individual gas Ptotal = P 1 + P 2 + P 3

Example Two gases are pumped into a 32. 0 L reaction vessel at 25. 0 C one after another. 6. 20 mol of O 2(g) is pumped in first, then 8. 30 mol of H 2(g) is pumped in. What would the pressure gauge reading be after each gas is pumped in? O 2(g) n = 6. 20 mol T = 25. 0 C = 298. 15 K V = 32. 0 L R = 8. 314 k. Pa L/mol K PV = n. RT P(32. 0 L) = (6. 20 mol)(8. 314 k. Pa L/mol K)(298. 15 K) P = 480. 2…k. Pa 1 st reading = 480 k. Pa

O 2(g) + H 2(g) n =6. 20 mol + 8. 30 mol = 14. 5 mol T = 25. 0 C = 298. 15 K V = 32. 0 L R = 8. 314 k. Pa L/mol K PV = n. RT P(32. 0 L) = (14. 5 mol)(8. 314 k. Pa L/mol K)(298. 15 K) P = 1123. 2…k. Pa 2 nd reading = 1. 12 x 103 k. Pa

Or you can calculate the pressure of oxygen, then the pressure of hydrogen separately and add the pressure’s together to get the same answer. This follows Dalton’s Law of Partial Pressures. Give it a try:

C. Ideal Gases and Real Gases ¬for ideal gases we assume that there are no between the intermolecular attractions molecules of the gas ¬in real gases, however, there attractions between the molecules ¬we don’t have to worry about considering this in our calculations because at standard P and T conditions, the molecules are very far apart and are moving very quickly they don’t interact much with each other

¬real gases behave like ideal gases at high temperatures and low pressures ¬real gases deviate from ideal gas behaviour at very low temperatures (moving very slowly) and very high pressures (molecules close together)

Review assignment p. 156 #1 -25 (omit 12, 21, 24)