Gases Part II General Properties of Gases 1






















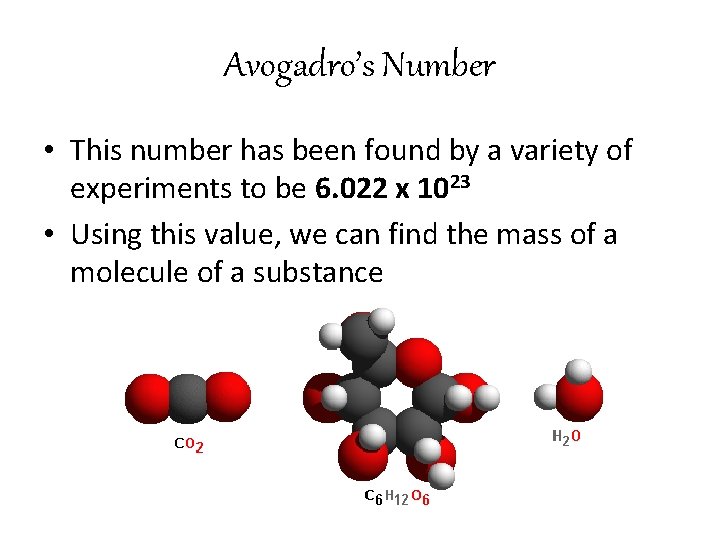
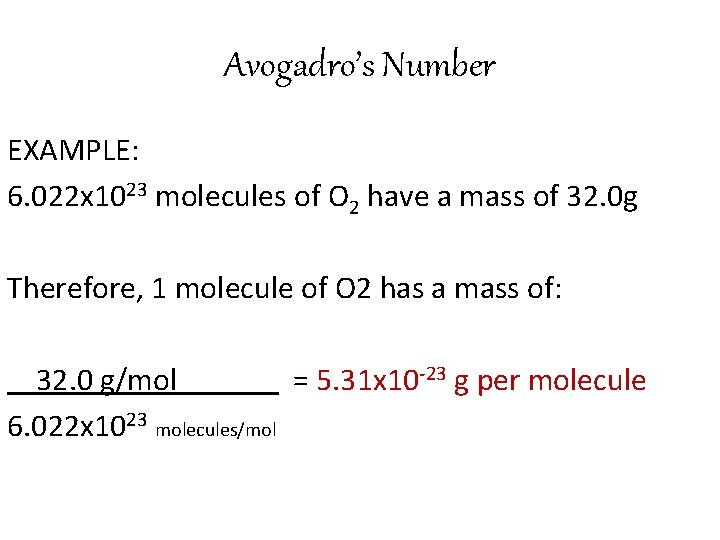














- Slides: 44

Gases Part II

General Properties of Gases 1) Gases are compressible 2) Gases fill any container 3) Different gases mix completely 4) Gases expand on heating 5) Gases do not settle in their container

Kinetic-Molecular Theory • According to this theory, gases consist of individual molecules that are relatively far apart with a lot of empty space between them.

1) Gases are compressable • The particles are very small, so that the volume occupied by the gas molecules can be ignored because it is insignificant when compared with the volume of the container the gas is contained in • This explains the ease with which gases can be compressed

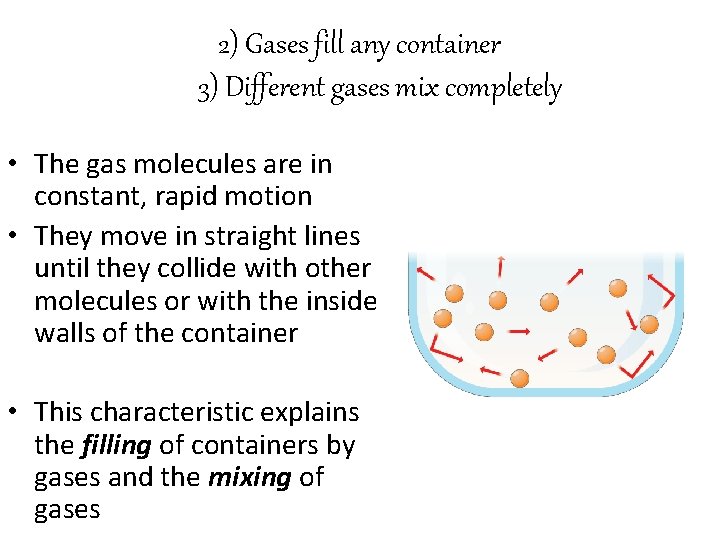
2) Gases fill any container 3) Different gases mix completely • The gas molecules are in constant, rapid motion • They move in straight lines until they collide with other molecules or with the inside walls of the container • This characteristic explains the filling of containers by gases and the mixing of gases

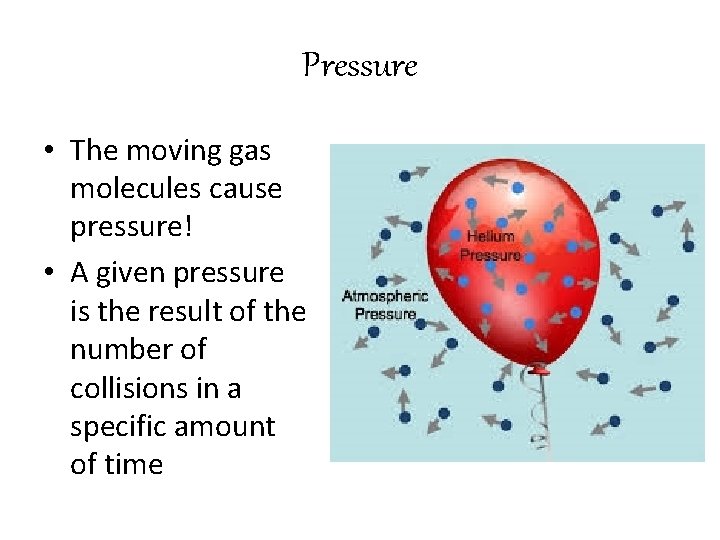
Pressure • The moving gas molecules cause pressure! • A given pressure is the result of the number of collisions in a specific amount of time

Gas Pressure is Increased by: • Forcing more gas into a container – Thus, increasing the number of collisions per unit time • Decreasing the volume of the gas by decreasing the size of the container – Thus, shortening the average distance between the molecules and therefore the number of collisions • Heating the gas in a closed container – Thus increasing the speed of the molecules and therefore the number of collisions

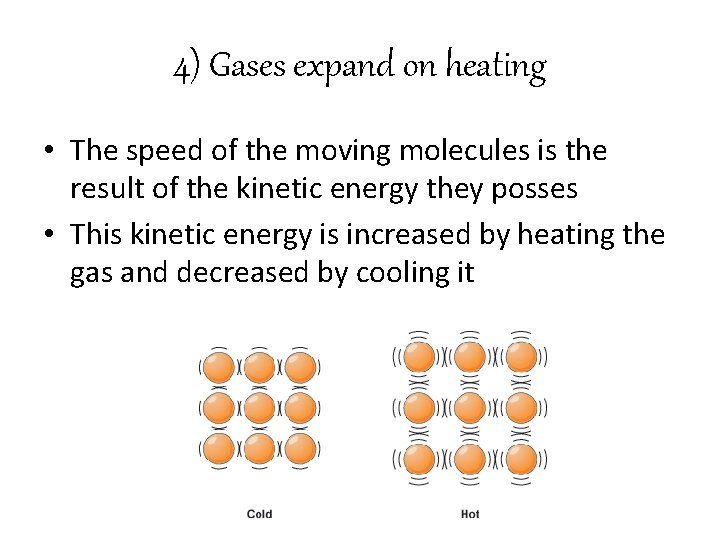
4) Gases expand on heating • The speed of the moving molecules is the result of the kinetic energy they posses • This kinetic energy is increased by heating the gas and decreased by cooling it

Kinetic-Molecular Theory • The kinetic-molecular theory suggest that the collisions of the gas molecules with other molecules or with the walls of the container are perfectly elastic - they take place without loss of energy

5) Gases do not settle in their container • If there were energy loses in these collisions, a loss of kinetic energy would result and the gas would settle in its container • Elastic collisions explains the fact that gases do not settle

Ideal Gases • Student Notes from pg. 69 -70

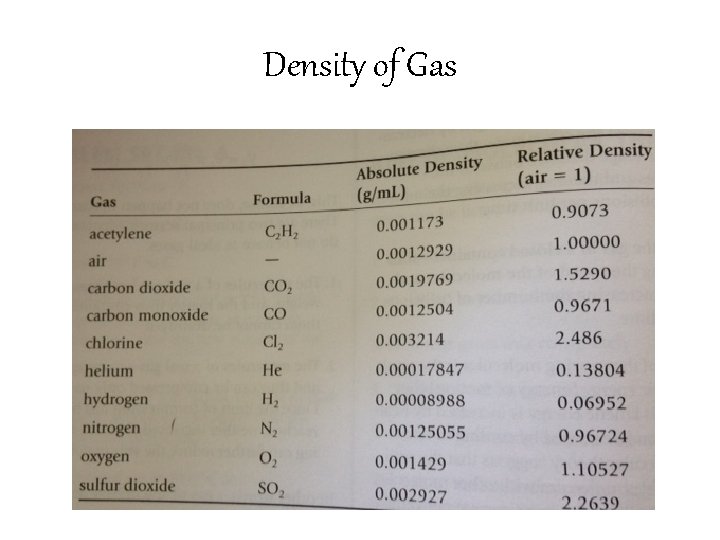
Density of Gases • The absolute density of a gas is the mass in grams of 1 m. L of the gas at standard conditions • Gases have a very low density (molecules are not close together because of all of the empty space!)

Density of Gases • The density of a gas can be calculated by finding the actual mass of a known volume of gas at a known temperature and pressure.

Density of Gases EXAMPLE: a 564. 3 m. L volume of chlorine gas at 27*C and 740 Torr has a mass of 1. 607 g. Find the density of chlorine. First, the volume must be reduced to standard conditions: V 1= 564. 3 m. L P 1= 740 Torr V 2= 500 m. L P 2= 760 Torr T 1= 300 K T 2= 273 K 740(564. 3)(273) = V 2(760)(300) = 500 m. L

EXAMPLE: a 564. 3 m. L volume of chlorine gas at 27*C and 740 Torr has a mass of 1. 607 g. Find the density of chlorine V 1= 564. 3 m. L V 2= 500 m. L P 1= 740 Torr P 2= 760 Torr T 1= 300 K T 2= 273 K • Density is the mass of 1 m. L of the gas at standard conditions. • Because 500 m. L of chlorine at standard conditions has a mass of 1. 607 g we can find the mass of 1 m. L with a simple proportion: x = 1. 607 g 1 m. L 500 m. L x= 0. 003214 g/m. L The density of chlorine!

0. 003214 g/m. L The density of chlorine!

Density of Gas • Because the absolute densities of gases involve such small numbers, they are often compared with the density of air. • Relative density is the comparison indicating the number of times a gas is more dense than air

Density of Gas

What is a Mole? • SI unit which measures the number of particles in a specific substance • Abbreviated as mol

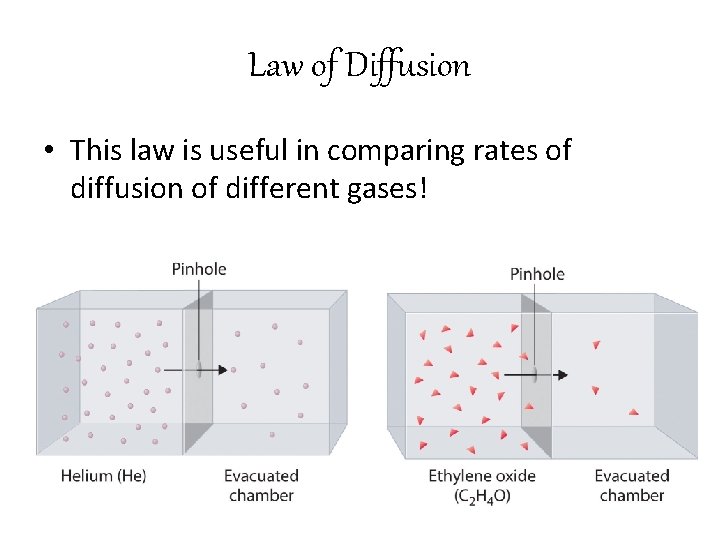
Law of Diffusion • Gas molecules are small enough to diffuse through many materials • In 1846 Thomas Graham discovered that: – rates of diffusion of gases are inversely proportional to the square root of their molar mass when the gases are at the same temperature and pressure

Law of Diffusion • This law is useful in comparing rates of diffusion of different gases!

Law of Diffusion EXAMPLE: How much faster will hydrogen diffuse than helium? (H 2 and He) From the periodic table we find the molar mass of each gas: Helium: 4 u Hydrogen: 2 u Hydrogen rate = sqrt(4/2) = 1. 41 Helium rate Thus, hydrogen diffuses about 1. 4 times as fast as helium

Law of Diffusion • Graham’s Law of Diffusion was put to use in creating the original atomic bomb. • Molecules of gas containing the uranium isotope U 235 diffused faster than U 238. • Why?

Gram Molecular Volume • From the density of a gas, we can find what volume a mole of the gas will occupy at standard conditions.

Gram Molecular Volume Example: Hydrogen Density of hydrogen = 0. 00008988 g/m. L Gram molecular mass: 2. 016 g (mass of 1 mol of H 2 = 2 x 1. 00 g/mol) 0. 00008988 g = 2. 016 g 1 m. L x X= 22, 400 m. L

Gram Molecular Volume • Calculations of other gases yield the same results. • Thus, for any gas, the volume occupied at standard conditions by 1 mol of the gas is 22. 4 L • This is significant! Now we can see that when we talk about a mole of gas, we are referring to both a definite mass of a gas (molecular mass) and a definite volume (22. 4 L) at standard conditions!

Avogadro’s Number • Avogadro’s Law states that equal volumes of gases contain equal numbers of molecules. • This is because at standard conditions 1 mol of any gas occupies the same gram molecular volume, 1 mol of every molecular substance must contain the same number of molecules
Avogadro’s Number • This number has been found by a variety of experiments to be 6. 022 x 1023 • Using this value, we can find the mass of a molecule of a substance
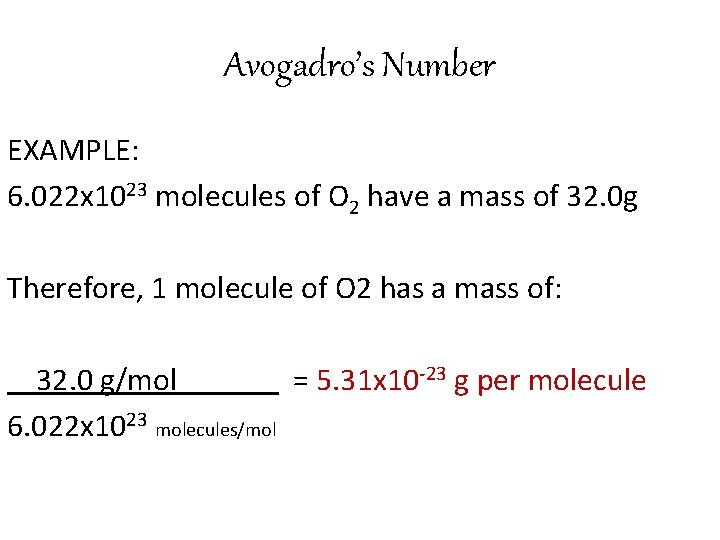
Avogadro’s Number EXAMPLE: 6. 022 x 1023 molecules of O 2 have a mass of 32. 0 g Therefore, 1 molecule of O 2 has a mass of: 32. 0 g/mol = 5. 31 x 10 -23 g per molecule 6. 022 x 1023 molecules/mol

Scientific Notation 5. 31 x 10 -23 g per molecule is 0. 00000000000531 g per molecule of O 2 So a single molecule of O 2 would be 2. 65 x 10 -23 grams

Finding Molecular Masses We must: • Find the weight of a substance – At a known volume – in the gaseous state – at known temp and pressure • Reduce the volume to standard conditions • Calculate the weight of 22. 4 L at STP using a proportion

Finding Molecular Masses • The direct weighing of gases is difficult • So we actually use a solid or liquid substance that will decompose to produced the desired gas is weighed before and after decomposition • The loss in weight is then the weight of the gas.

Finding Molecular Masses • EXAMPLE: A 7. 00 g portion of KCl. O 3 is heated and produces 1. 55 L of oxygen gas at 27*C and 756 Torr. The residue from the heating has a mass of 5. 00 g. Find the molecular mass of oxygen. Mass of oxygen: 7. 00 – 5. 00 = 2. 00 g Volume of oxygen at standard conditions: P 1 = 756 Torr P 2 = 760 Torr V 1 = 1. 55 L V 2 = ? ? ? T 1 = 300 K T 2 = 273 K

Finding Molecular Masses • EXAMPLE: A 7. 00 g portion of KCl. O 3 is heated and produces 1. 55 L of oxygen gas at 27*C and 756 Torr. The residue from the heating has a mass of 5. 00 g. Find the molecular mass of oxygen. Mass of oxygen: 7. 00 – 5. 00 = 2. 00 g Volume of oxygen at standard conditions: 1. 40 L P 1 = 756 Torr P 2 = 760 Torr V 1 = 1. 55 L V 2 = ? ? ? T 1 = 300 K T 2 = 273 K 756(1. 55)(273) = 760(V 2)300 = 1. 40 L But remember, we need The molecular mass!

Finding Molecular Masses • EXAMPLE: A 7. 00 g portion of KCl. O 3 is heated and produces 1. 55 L of oxygen gas at 27*C and 756 Torr. The residue from the heating has a mass of 5. 00 g. Find the molecular mass of oxygen. Mass of oxygen: 7. 00 – 5. 00 = 2. 00 g Volume of oxygen at standard conditions: 1. 40 L By proportion, the molecular weight of oxygen is: 1. 40 L = 22. 4 L 2. 00 g x x= 32. 0 g

Practice A 9 g sample of Na. OH is heated and produces 1. 67 L of oxygen gas at 27*C and 745 Torr. The residue from the heating has a mass of 4 g. Find the molecular mass of oxygen. 75. 15 g

Practice A 4. 32 g sample of SO 4 is heated and produces 4. 20 L of oxygen gas at 24*C and 732 Torr. The residue from the heating has a mass of 3. 23 g. Find the molecular mass of oxygen. 0. 69 g

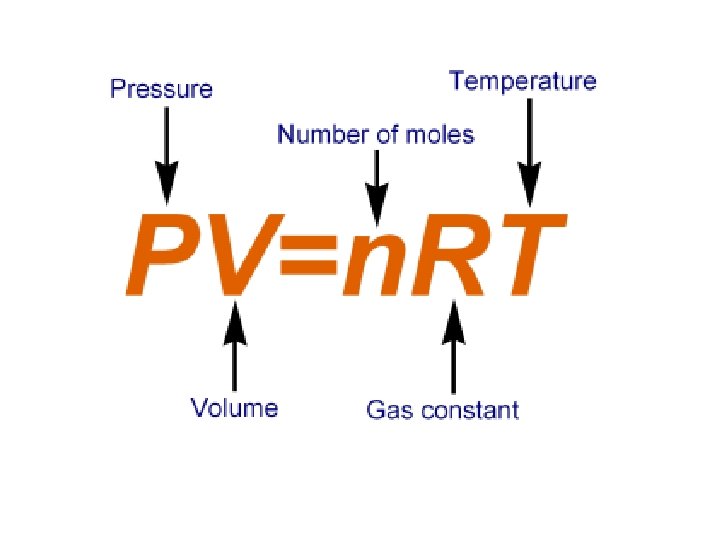
The Ideal-Gas Equation • The gas laws (Boyle’s, Charles’s, Combined, Avagadros) all assume a fixed amount of gas • But often, the number of moles of gas changes! • Thus, we must use the ideal-gas equation.


Ideal Gas Constant • Any units may be chosen for pressure and volume, but the value of the idea constant will depend on the units chosen • Most commonly, the pressure is expressed in atmospheres (atm) and volume in liters. • In this case the idea-gas constant is: R= 0. 0821 L x atm K x mol

Ideal Gas Equation Example An 88 g sample of CO 2 would occupy what volume at a pressure of 2. 5 atm and a temperature of 27*C? First we convert the grams of CO 2 to moles: 88 g x 1 mol = 2. 0 mol 1 44. 0 g Next, we convert the temp to Kelvin: 27*C + 273 = 300 K

Example An 88 g sample of CO 2 would occupy what volume at a pressure of 2. 5 atm and a temperature of 27*C? P= 2. 5 atm V= ? n = 2. 0 mol R = 0. 0821 L x atm / K x mol (constant) T = 300 K 19. 7 L

On Your Own • Given the following sets of values, calculate the unknown quantity P= 1. 01 atm V= ? N = 0. 00831 mol T = 25*C 0. 20 L

On Your Own • At what temperature would 2. 10 moles of N 2 gas have a pressure of 1. 24 atm and in a 25. 0 L tank? 181 K