Gases Chapter 5 Things to know about gases

Gases Chapter 5

Things to know about gases n n n Have no specific volume-volume of the gas is the volume of the container Temperature must be in Kelvin Barometers measure atmospheric pressure q q q n 760 mm Hg 1 atm 101. 3 k. Pa STP

Charles’ Law n Volume is directly proportional to absolute temperature

Boyle’s Law n n Volume is inversely proportional to pressure P 1 V 1 = P 2 V 2 http: //www. grc. nasa. gov/WWW/K-12/airplane/Animation/frglab 2. html

Gay-Lussac’s Law n Pressure is directly proportional to absolute temperature

Ideal Gas Law n n n P = pressure (atm) V = volume (L) n = moles R = 0. 0821 T =temperature (K) PV = n. RT

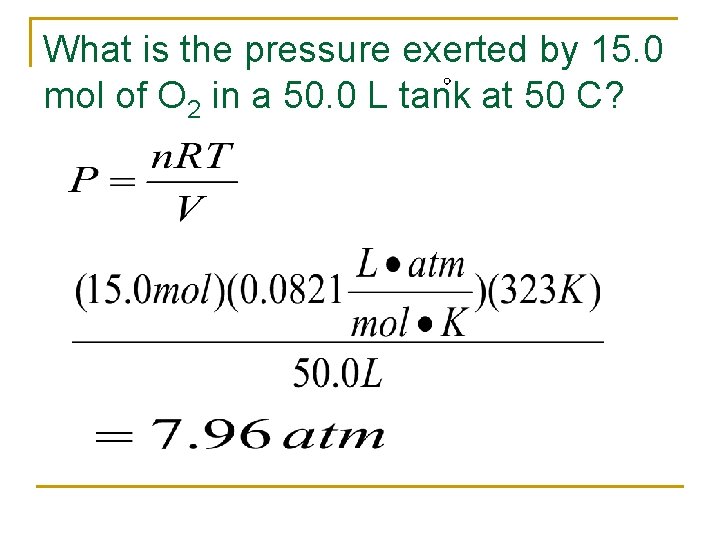
What is the pressure exerted by 15. 0 mol of O 2 in a 50. 0 L tank at 50 C?

n GMM = molar mass d = density = mass/volume (g/L) R = 0. 0821 n T = temperature (K) n n

Determine the density of O 2 at 27 C and 735 mm Hg

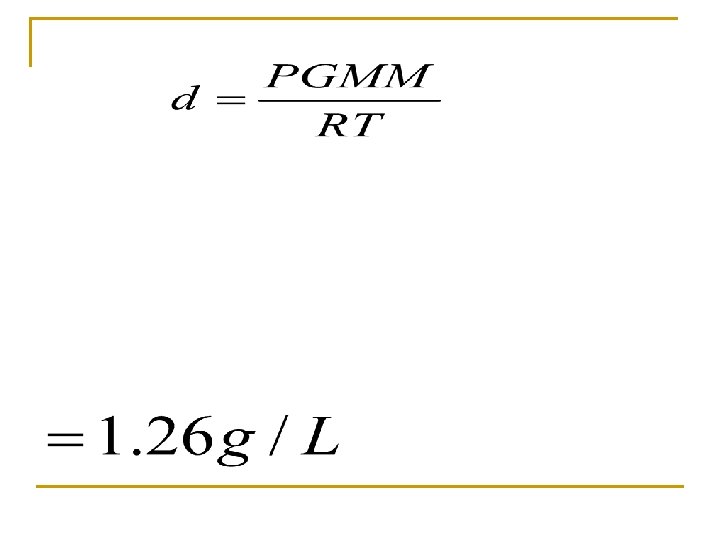
Density of a gas n n n Compressing a gas increases its density Increasing temperature decreases density-hot air rises Hydrogen is the least dense gas of all because it has the lowest GMM--greatest lifting power

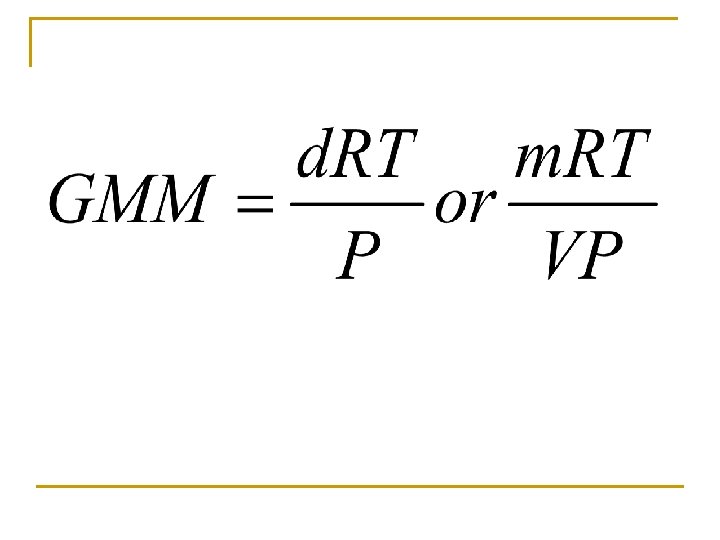
A flask weighs 52. 693 g empty and 53. 117 g when filled with acetone vapor at 100 C and 752 mm Hg. Taking the volume of the flask to be 226. 2 m. L calculate the molar mass of acetone.

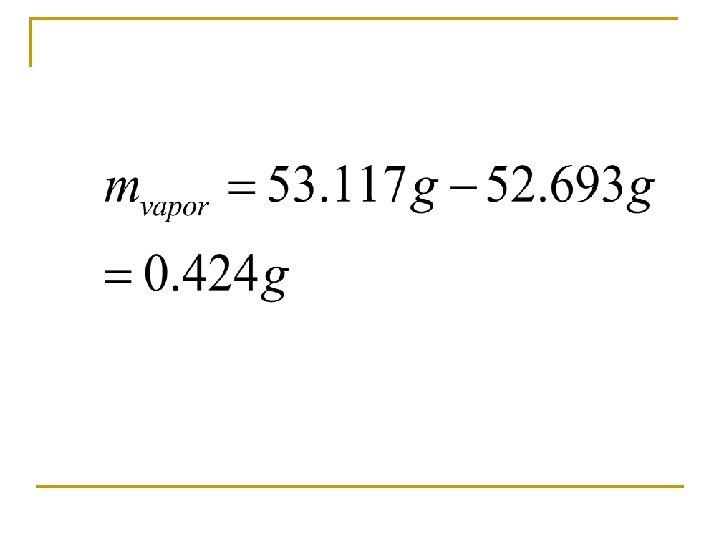
Gases in reactions n First law of Gases. . . Gas Laws only work for Gases!

Determine the mass of zinc metal required to react with HCl to form 16. 0 L H 2 (g) at 20 C and 735 mm Hg

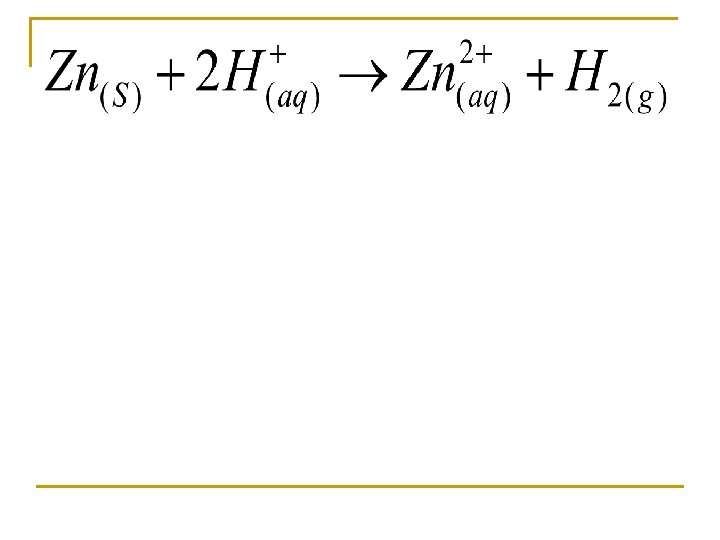
Dalton’s Law of Partial Pressures n The total pressure of a gas mixture is the sum of partial pressures of the components of the mixture. q n Ptotal = P 1 + P 2 +. . . Used when gases are collected over water q Pgas =Ptotal - Pwater vapor n Pwater vapor is the vapor pressure of water at the specified temperature.

A student prepares a sample of hydrogen gas by electrolyzing water at 25 C. She collects 152 ml of hydrogen over water at a pressure of 758 mm Hg, calculate the moles of hydrogen collected. Look up the vapor pressure of water at 25 C from appendix 1. Pwater = 23. 76 mm Hg. 758 mm Hg – 23. 76 mm. Hg = 734 mm Hg

Now solve for moles of hydrogen with the ideal gas law.

Partial pressure and mole fractions n Mole fraction = X q n Xa = na/ntotal Partial pressure of a gas in a mixture is equal to its mole fraction multiplied by the total pressure q Pa = Xa. Ptotal

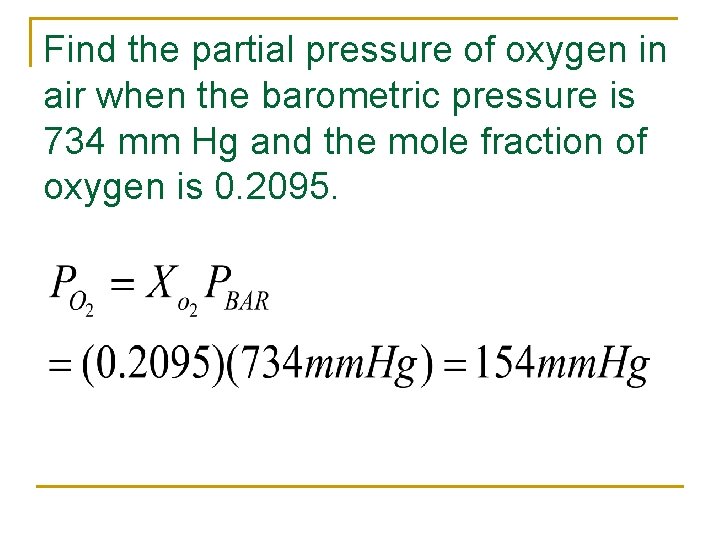
Find the partial pressure of oxygen in air when the barometric pressure is 734 mm Hg and the mole fraction of oxygen is 0. 2095.

Kinetic theory of Gases n n Gases are mostly empty space Gas molecules are in constant random motion q q n They collide with each other and the sides of the container Collisions are elastic Gas pressure is caused by the collisions with the walls of the container q Increase P increases the number of collisions

Expression for pressure n n The ratio N/V is the concentration of gas mc in the container. The more mc, the more collisions, the more P. mu 2 is the measure of the energy of the collisions.

Average kinetic energy of translational motion Et n At a given T molecules of different gases must all have the same Et n Et of a molecule is directly proportional to the T in Kelvin T is the only variable! n q q R = 0. 0821 NA = 6. 022 X 1023

Average speed, u

Constant GMM aka the same gas

At constant temperature

Graham’s Law n Effusion q n The flow of gas molecules at low pressures through tiny pores or pinholes. At a given temperature the rate of effusion of a gas is inversely proportional to the square root of its molar mass

What does this mean? n n A lighter gas will have a faster rate. Can be used to separate isotopes

Real gases n The closer a gas is to the liquid state (high P low T) the more it will deviate from the ideal gas law because q Of the attractive forces between gas molecules n n q Gives a smaller molar volume (<22. 4 L/mol) than predicted The larger the attractive forces the bigger the deviation The finite volume of gas particles n Gives a larger molar volume (>22. 4 L/mol) predicted because gases can only get so close