Gases Chapter 12 Properties of Gases Compressibility Mass

Gases Chapter 12

Properties of Gases Compressibility Mass Volume (fill container) Exert Pressure Diffuse through other gases Low Density

Kinetic Molecular Theory (KMT) 1. 2. 3. 4. 5. 6. All gases are matter (have mass and take up space). These particles are in constant, rapid and random motion. All collisions are perfectly elastic. (no energy is lost in the collision) The force of gas particle collisions on the walls of the container creates pressure; however, gas particles do not exert force on each other. At a given temperature, all gas particles have the same amount of kinetic energy (temperature). The distance between gas particles is very large.

Gas Pressure Gas pressure results from the force of colliding particles on a given area. The metric unit of force is the newton (similar to the ounce in the English system). A newton of force acting on a square meter is called a pascal. Normal atmospheric pressure at sea level is 101. 3 k. Pa.

Measuring Gases In order to describe a gas, we use four variables to make predictions about the behavior of the particles. 1. Amount of a gas (n) expressed in moles 2. Amount of space the gas takes up, volume (V), as measured in liters. *note: this is the volume of the container 3. Measure of kinetic energy, temperature (T), in degrees Kelvin 1. *note: K = C + 273 4. Measure of the force exerted by the gas particles on the walls of the container, pressure (P)

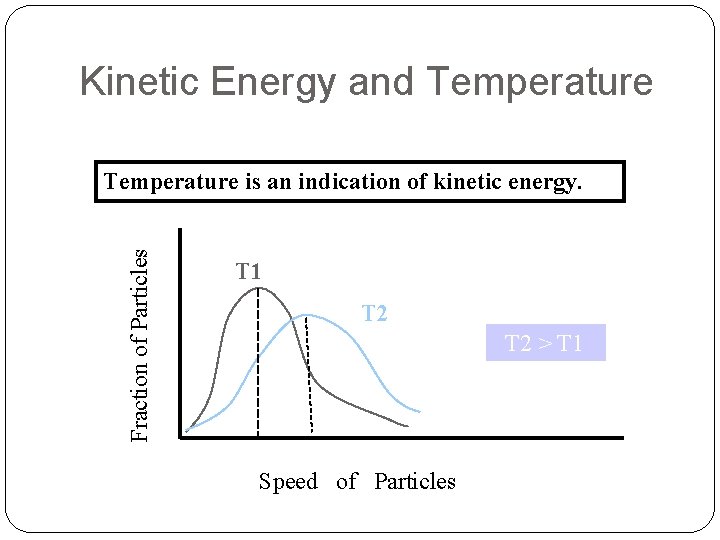
Kinetic Energy and Temperature Fraction of Particles Temperature is an indication of kinetic energy. T 1 T 2 > T 1 Speed of Particles

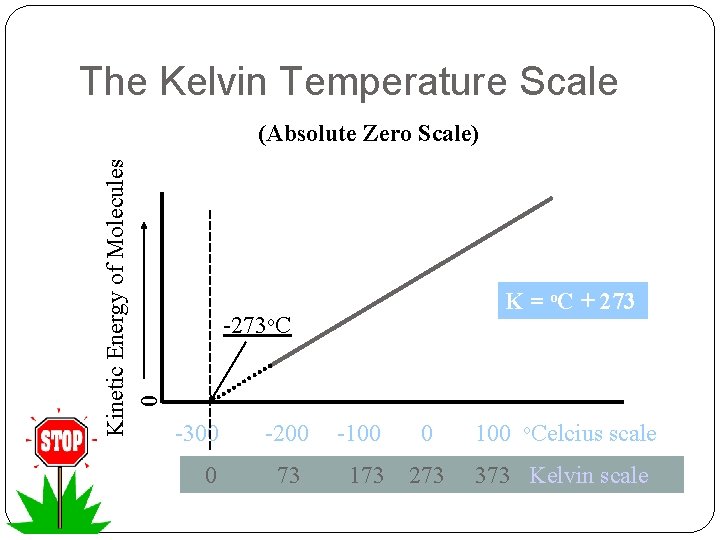
The Kelvin Temperature Scale Kinetic Energy of Molecules 0 (Absolute Zero Scale) K = o. C + 273 -273 o. C -300 0 -200 73 -100 173 0 100 o. Celcius scale 273 373 Kelvin scale

Pressure is the measure of the amount of force of an object per unit area. Newton / m 2 = Pascal Atmospheric Pressure is the amount of pressure exerted by the entire atmosphere on the surface of the Earth. A barometer is an instrument that measures atmospheric pressure A manometer is an instrument that measures the pressure of an enclosed gas

Mercury Barometer

Manometer

STP Pressure and temperature changes affect gas volume. To compare experimental results, scientist convert their results to standard temperature and pressure (STP) Standard Conditions: Standard Temperature = 0 o. C (273 K) Standard Pressure = 101. 3 k. Pa (1 atm) {760 torr}

Pressure Units Kilopascals (k. Pa) Atmospheres (atm) 1 atm = 101. 3 k. Pa Torricellis (torr) 1 torr = 1 mm Hg 760 torr = 101. 3 k. Pa (other units are listed on page 420)

Pressure Units Atmosphere (atm) Millimeter Hg (mm. Hg) Pascal (Pa) Pounds per square inch (psi) Kilopascal (k. Pa) 1 atm = Standard Pressure 1 atm = 760 mm. Hg 1 atm = 101, 325 Pa 1 atm = 14. 7 psi 1 atm = 101. 3 k. Pa

Conversions Covert using Dimensional Analysis Information you have x conversion factor (unknown/known) Convert 665 mm. Hg to k. Pa 665 mm. Hg x 101. 3 k. Pa = 88. 6 k. Pa 760 mm. Hg Classwork: page 421 #1 -4 Homework: page 422 #1 -12

Boyle’s Law Pressure and Volume are inversely proportional at a given temperature and number of molecules. VP = k (a constant value)

Pressure Effects on Volume V 1/P

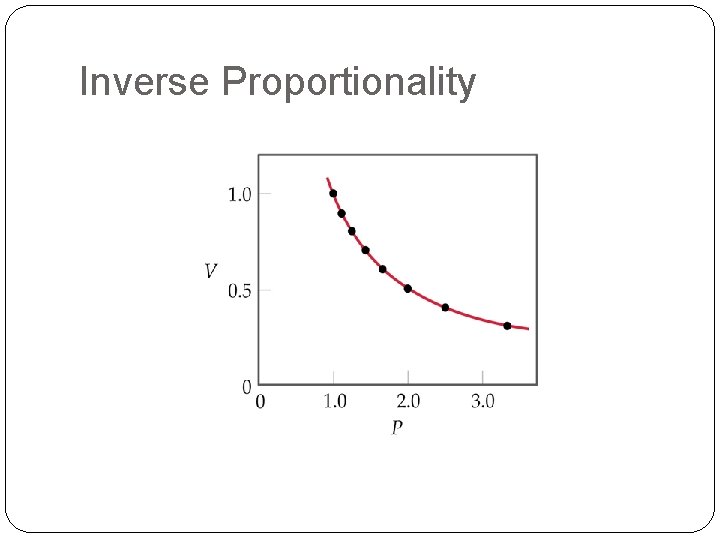
Inverse Proportionality

Boyle’s Law continued V 1 P 1 = k 1 and V 2 P 2 = k 2 since k 1 = k 2 (that’s why its called a constant) V 1 P 1 = V 2 P 2 This is the mathematical expression for Boyle’s Law

A Boyle’s Law Problem A gas in a 242 cm 3 container exerts a pressure of 87. 6 k. Pa. What volume would the gas occupy at standard atmospheric pressure? Identify Variables V 1 = 242 cm 3 V 2 = ? P 1 = 87. 6 k. Pa P 2 = 101. 3 k. Pa

Two Methods of Solving 1. Algebraic: V 1 P 1 = V 2 P 2 V 2 = V 1 P 1 P 2 V 2 = 242 cm 3 x 87. 6 k. Pa 101. 3 k. Pa V 2 = 209 cm 3

Another Method 2. Logic and reason: The new volume (V 2) depends upon the old volume (V 1) multiplied by a pressure change. 87. 6 V 2 = 242 cm 3 x _______ 101. 3 Since the pressure is increasing, the volume should decrease. Multiply by a fraction less than 1.

Charles’s Law At a given pressure and number of molecules, Volume and Temperature are directly proportional. V = k T

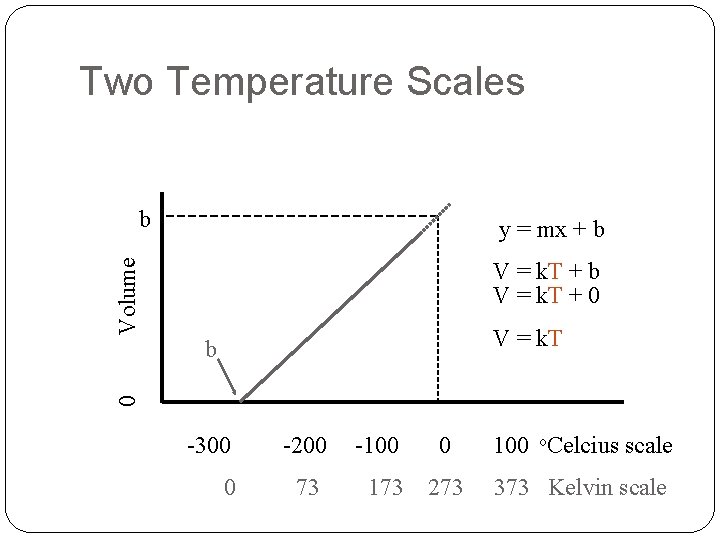
Two Temperature Scales b y = mx + b Volume V = k. T + b V = k. T + 0 V = k. T 0 b -300 0 -200 73 -100 173 0 100 o. Celcius scale 273 373 Kelvin scale

Charles’s Law Continued V 1 = k 1 T 1 V 2 = k 2 T 2 V 1 = V 2 T 1 T 2 and since k 1 = k 2 This is the mathematical expression for Charles’s Law

A Charles’s Law Problem A 225 cm 3 volume of gas is collected at 58 o. C. What volume would the gas occupy at standard temperature? Identify Variables V 1 = V 2 = 225 cm 3 ? T 1 = 58 o. C + 273 = 331 K T 2 = 0 o. C + 273 = 273 K

Two Methods of Solving 1. Algebraic: V 1 / T 1 = V 2 / T 2 V 2 = V 1 T 2 T 1 V 2 = 225 cm 3 x 273 K 331 K V 2 = 186 cm 3

The Other Method 2. Logic and reason: The new volume (V 2) depends upon the old volume (V 1) multiplied by a temperature change. 273 V 2 = 225 cm 3 x _______ 331 Since the temperature is decreasing, the volume should decrease. Multiply by a fraction less than 1.

Gay-Lussac’s Law P 1 = k 1 T 1 and P 2 = k 2 T 2 P 1 = P 2 T 1 T 2 since k 1 = k 2 This is the mathematical expression for Gay-Lussac’s Law

The Combined Gas Law In most laboratory situations, both temperature and pressure change. The Combined Gas Law is used to calculate the affects of these changes.

A Combination of Gas Laws Boyle’s Law: V 1/P Charles’s Law: V T Gay-Lussac’s Law: P T V T/P To change a proportionality to an equality… multiply by a proportionality constant. V = k. T P V 1 P 1 = V 2 P 2 VP = k T 1 T 2 T

V 1 P 1 = V 2 P 2 T 1 T 2 Solve for each variable V 2 = V 1 P 1 T 2 / T 1 P 2 T 2 = V 2 P 2 T 1 / V 1 P 1 P 2 = V 1 P 1 T 2 / T 1 V 2

Sample Problem What volume would 955 cm 3 of a gas measured at 58 o. C and 108. 0 k. Pa occupy at 76 o. C and 123. 0 k. Pa? 955 cm 3 V 1 = ? V 2 = 331 K T 1 = 349 K T 2 = 108. 0 k. Pa P 1 = P 2 = 123. 0 k. Pa

Method #1 V 1 P 1 / T 1 = V 2 P 2 / T 2 V 2 = V 1 P 1 T 2 / (T 1 P 2) V 2 = (955 cm 3) (108. 0 k. Pa) (349 K) (331 K) (123. 0 k. Pa) V 2 = 884 cm 3

Method #2 108 349 x ----V 2 = 955 cm 3 x ----331 temperature increases volume increases pressure increases volume decreases V 2 = 884 cm 3 123

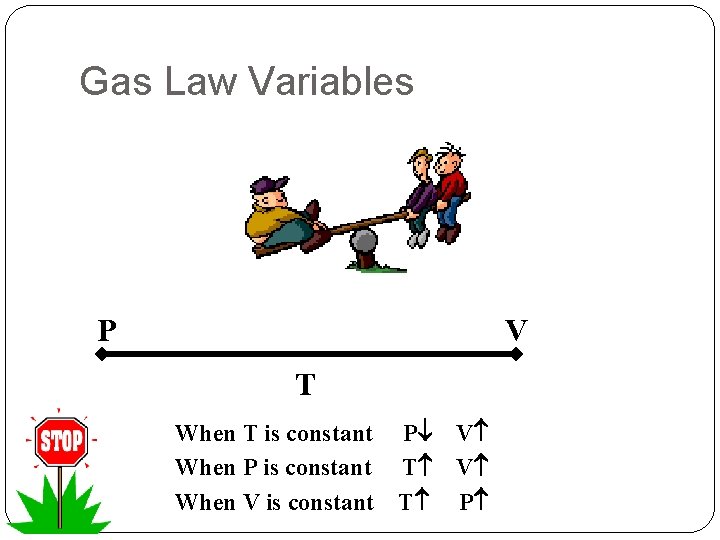
Gas Law Variables P V T When T is constant When P is constant When V is constant P T T V V P

Dalton’s Law of Partial Pressures Gases are often collected by water displacement. These gases contain water vapor. To find the pressure of the dry gas alone, Dalton’s Law of Partial Pressures is used. The total pressure exerted by a mixture of gases is equal to the sum of the partial pressures of each gas in the mixture.

Dalton’s Law of Partial Pressures Gases are often collected by water displacement. These gases contain water vapor. To find the pressure of the dry gas alone, Dalton’s Law of Partial Pressures is used. The total pressure exerted by a mixture of gases is equal to the sum of the partial pressures of each gas in the mixture.

The Mathematical Expression of Dalton’s Law PT = P 1 + P 2 + …. Pn Example: Gas A = 1. 0 atm Gas B = 1. 5 atm Gas C = 0. 5 atm PT = 3. 0 atm

The Pressure of a “Dry” Gas When a gas is collected over water, the total pressure is the result of the dry gas plus the water vapor pressure. PT = Pgas + Pvapor To determine the pressure of the dry gas alone, subtract the water vapor pressure from the total pressure. ( P. 401 ) Pgas = PT - Pvapor

Diffusion If a bottle of ammonia were opened at the front of the room, the odor could soon be detected at the back of the room. Diffusion is the random movement of particles through another substance. Effusion is gas under pressure escaping through a small opening.

Diffusion

Kinetic Energy The equation for finding the kinetic energy of a particle: K. E. = ½ mv 2 m = mass of the particle v = velocity (speed) of the particle

Kinetic Energy K. E. = ½ mv 2 #@*~!!* ~##~@!&

Graham’s Law If gases A and B are at the same temperature…. . ____ K. E. A = K. E. B ½ m. Av 2 A = ½ m. Bv 2 B m A v 2 A = m B v 2 B Collecting terms… v 2 A = m B v 2 B m. A v. A = v. B m. A This is the mathematical expression for Graham’s Law

The Meaning of Graham’s Law “The ratio of the velocities of two gases is equal to the square root of the inverse ratios of their masses. ” m. Av 2 A = m. Bv 2 B if: m. A > m. B then: v. B > v. A (The lightest gas always travels faster) See practice problems on page 438

A Graham’s Law Experiment HCl(g) + NH 3(g) NH 4 Cl(s) HCl v = d/t v. A = d. A/t. A v. B = d. B/t. B t. A = t. B v A / v B = d. A / d B (experimental) v. A / v. B = √m. B / m. A (accepted) % error: | exp. – accepted | x 100 accepted NH 3

Ideal Gases The gas laws we have studied only apply to ideal gases. There are no ideal gases.

Properties of Ideal Gases Ideal gases have: 1. Point mass (Particles have mass but occupy no volume) 2. No mutual attractions (No matter how close or how slow the particles are, they do not attract each other)

Ideal Gas Laws Work Real gas particles occupy negligible volume compared to the total volume occupied by the gas… (unless under very high pressures)

Real Gases

Ideal Gas Laws Work • Real gas particles occupy negligible volume compared to the total volume occupied by the gas… (unless under very high pressures) • Real gas particles have such weak intermolecular attraction forces that they do not affectively attract each other… (unless at very low temperatures)

Real Gas Laws Ideal gas laws work for real gases except at very high pressures or at very low temperatures. Why not use real gas laws that work all the time? Ideal gas law: PV = KT Solve for V Real gas law: [(P + n 2 a)/V 2] [V – nb] = KT Solve for V

The Real Gas Law Solution V = -(P + n 2 a) (P + n 2 a)2 – 4(KT)(P +n 2 a)(nb) 2 KT

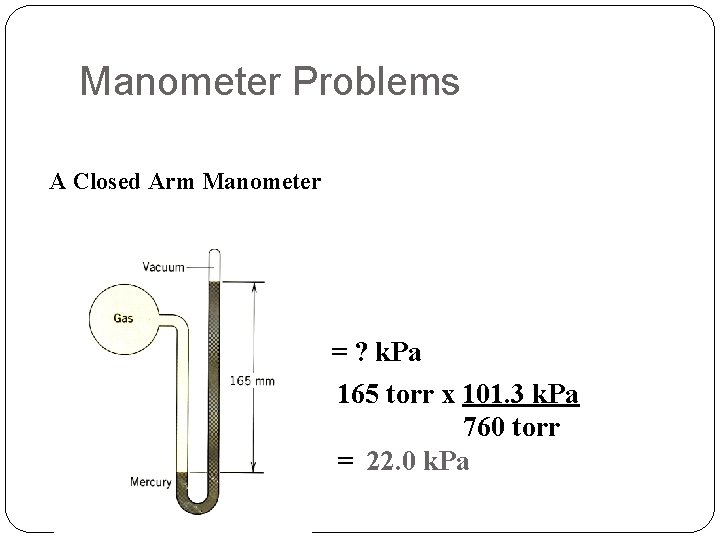
Manometer Problems A Closed Arm Manometer = ? k. Pa 165 torr x 101. 3 k. Pa 760 torr = 22. 0 k. Pa

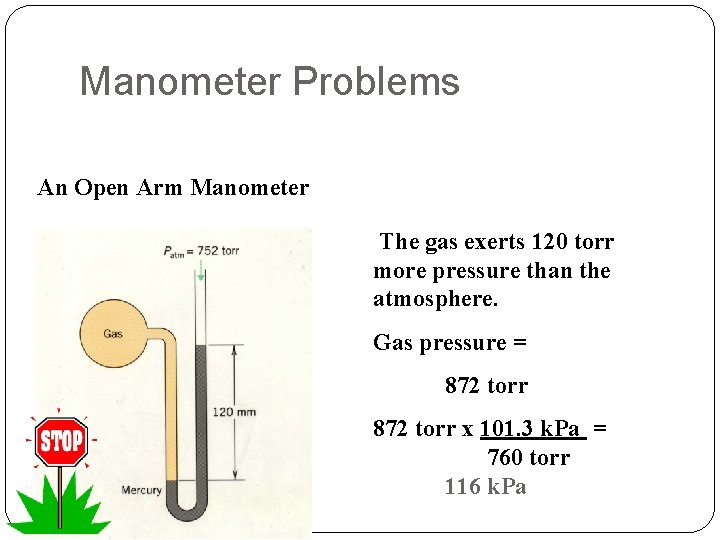
Manometer Problems An Open Arm Manometer The gas exerts 120 torr more pressure than the atmosphere. Gas pressure = 872 torr x 101. 3 k. Pa = 760 torr 116 k. Pa