Gas Pressure Gases exert pressure on any surface


![Units for Pressure • The SI-unit of pressure is Pascal [Pa] Atmospheres (atm) Millimeters Units for Pressure • The SI-unit of pressure is Pascal [Pa] Atmospheres (atm) Millimeters](https://slidetodoc.com/presentation_image_h/0629aa5bde19e9f44cae7c7ca5fe48bb/image-6.jpg)




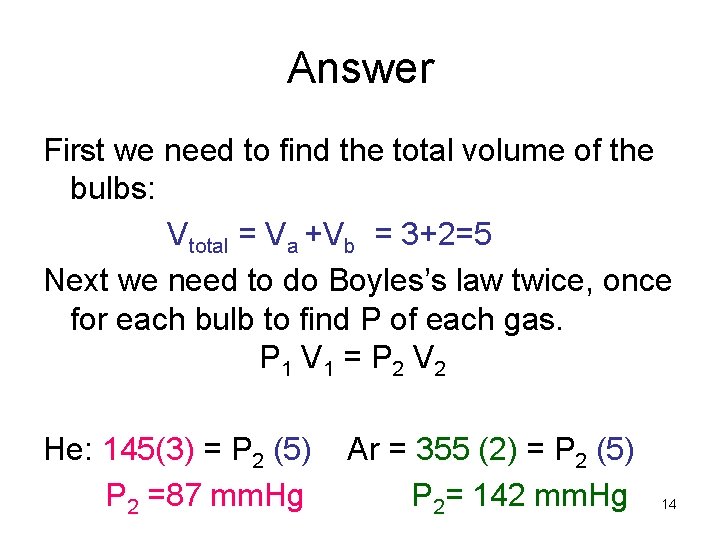






















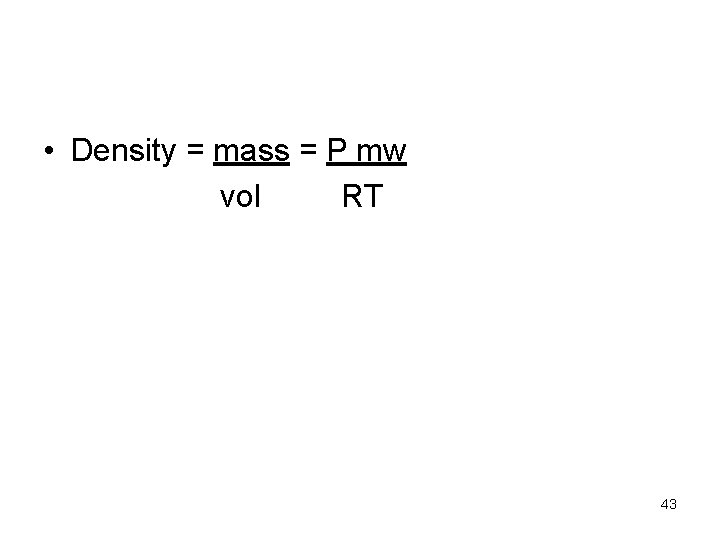





- Slides: 48

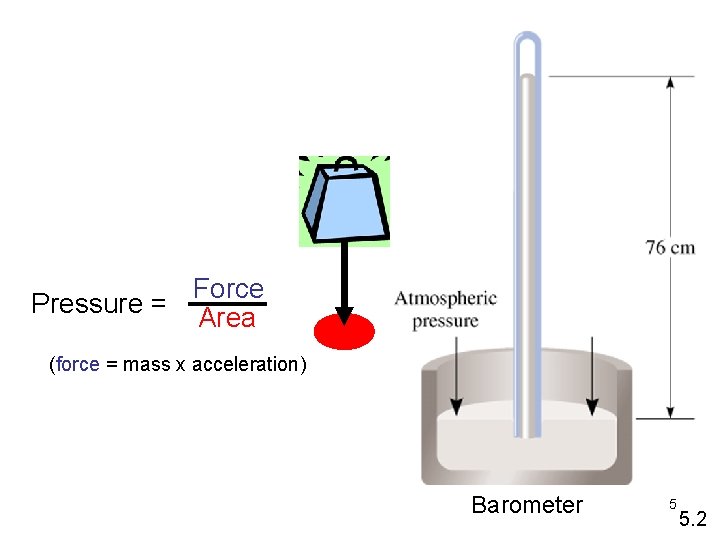
Gas Pressure • Gases exert pressure on any surface they come in contact with. • Pressure is related to the number of collisions the gas molecules have with wall of a container per unit of area per unit of time. • Pressure = Force / Area 1

Elements that exist as gases at 250 C and 1 atmosphere 2 5. 1

Physical Characteristics of Gases • Gases assume the volume and shape of their containers. • Gases are the most compressible state of matter. • Gases will mix evenly and completely when confined to the same container. • Gases have much lower densities than liquids and solids. 3 5. 1

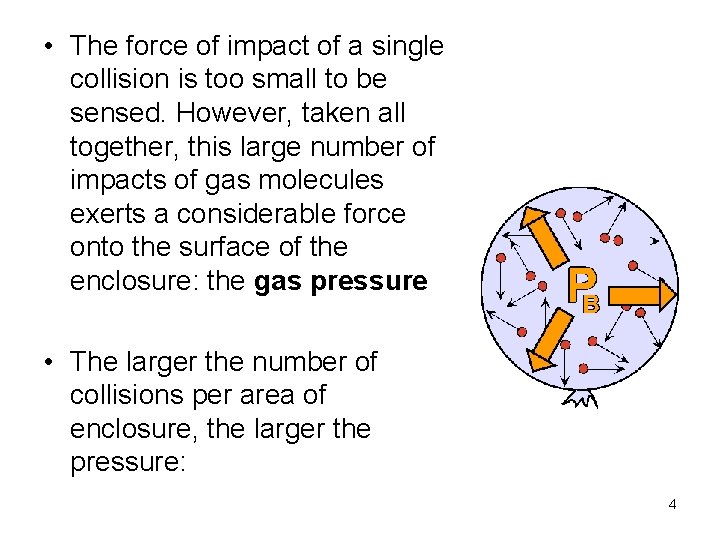
• The force of impact of a single collision is too small to be sensed. However, taken all together, this large number of impacts of gas molecules exerts a considerable force onto the surface of the enclosure: the gas pressure • The larger the number of collisions per area of enclosure, the larger the pressure: 4

Force Pressure = Area (force = mass x acceleration) Barometer 5 5. 2
![Units for Pressure The SIunit of pressure is Pascal Pa Atmospheres atm Millimeters Units for Pressure • The SI-unit of pressure is Pascal [Pa] Atmospheres (atm) Millimeters](https://slidetodoc.com/presentation_image_h/0629aa5bde19e9f44cae7c7ca5fe48bb/image-6.jpg)
Units for Pressure • The SI-unit of pressure is Pascal [Pa] Atmospheres (atm) Millimeters of Mercury (mm. Hg) Torr (torr) Pressure per square inch (Psi) = lbs/in 2 1 atm = 760 mm. Hg = 760 torr 1 atm = 1. 013 x 105 Pa 1 atm = 14. 69 psi 6

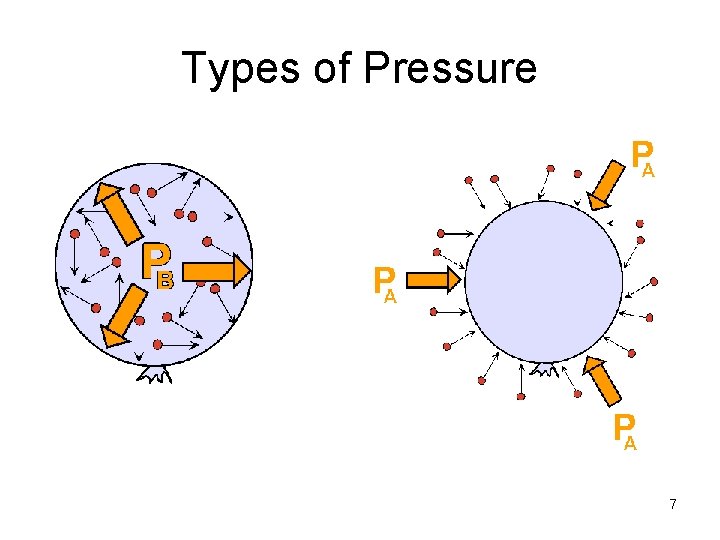
Types of Pressure 7

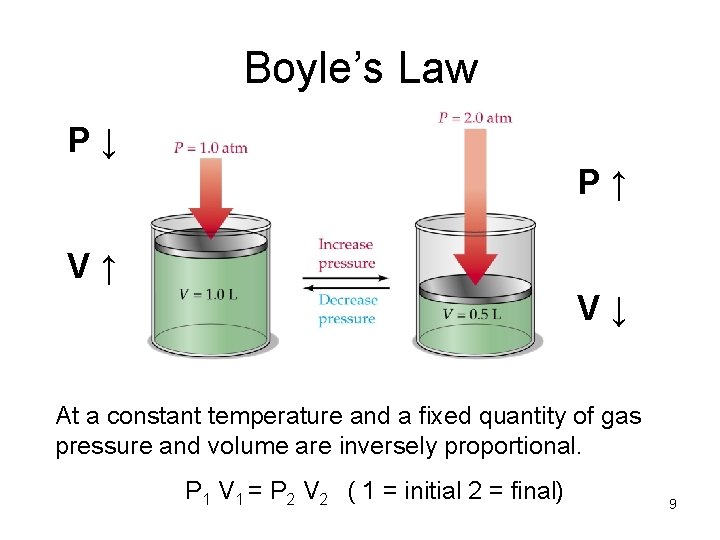
Boyles Law Demo lets assume that the balloon is tight, so that the amount or mass of air in it stays the same • Density = mass/ volume, • the gas density of the balloon thus varies only with its volume (when mass is held constant). • If we squeeze the balloon, we compress the air and two things will happen: – the air pressure in the balloon will increase. – the density of the air in the balloon will increase. • Since density is mass over volume, and the mass stays constant, the rise in density means that the volume of the balloon decreases: pressure goes up (↑); volume goes down (↓) • Pressure and volume are inversely proportional 8

Boyle’s Law P↓ P↑ V↑ V↓ At a constant temperature and a fixed quantity of gas pressure and volume are inversely proportional. P 1 V 1 = P 2 V 2 ( 1 = initial 2 = final) 9

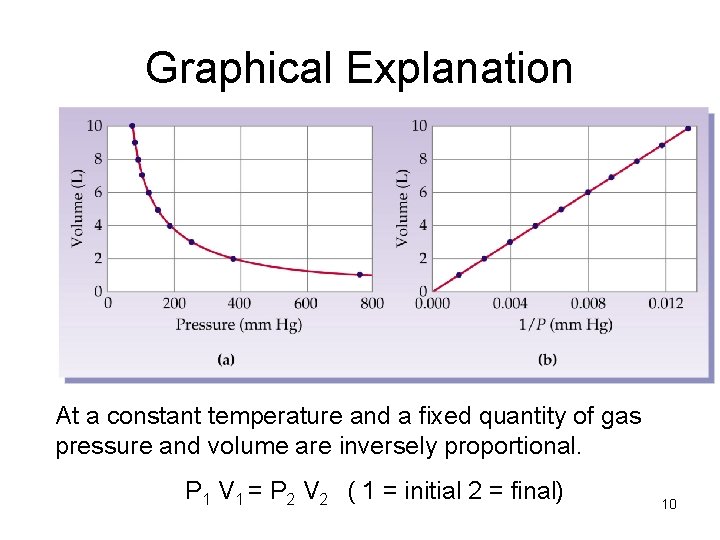
Graphical Explanation At a constant temperature and a fixed quantity of gas pressure and volume are inversely proportional. P 1 V 1 = P 2 V 2 ( 1 = initial 2 = final) 10

Boyle’s Example Mini Lab 11

Chemistry in Action: Scuba Diving and the Gas Laws P Depth (ft) Pressure (atm) 0 1 33 2 66 3 V 12 5. 6

Example • A 3. 0 L bulb containing He at 145 mm. Hg is connected by a value to a 2. 0 L bulb containing Ar at 355 mm. Hg. Calculate the partial pressure of each gas and the total pressure after the valve between the flasks is opened. 3. 0 L 2. 0 L Ar He 145 mm. Hg 355 mm. Hg 13
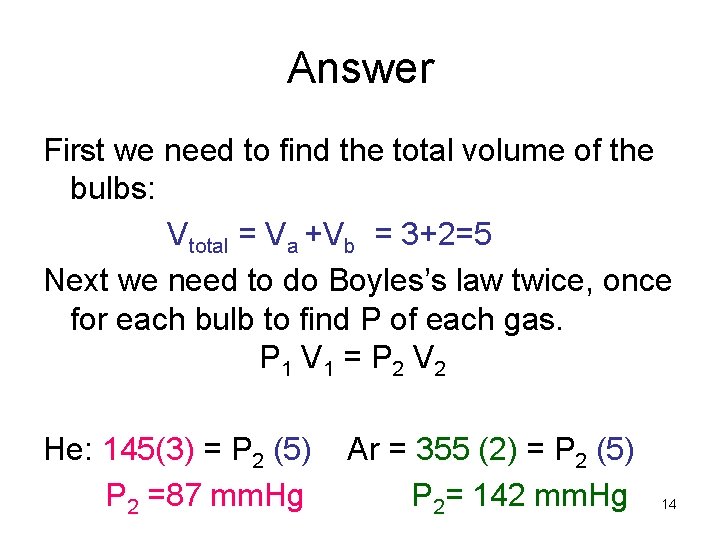
Answer First we need to find the total volume of the bulbs: Vtotal = Va +Vb = 3+2=5 Next we need to do Boyles’s law twice, once for each bulb to find P of each gas. P 1 V 1 = P 2 V 2 He: 145(3) = P 2 (5) P 2 =87 mm. Hg Ar = 355 (2) = P 2 (5) P 2= 142 mm. Hg 14

Answer Cont. He: 145(3) = P 2 (5) P 2 =87 mm. Hg Ar: 355 (2) = P 2 (5) P 2= 142 mm. Hg Now we need to find the after the valve between the two flasks is opened. Ptotal= P 2 He +P 2 Ar = 87 + 142 = 229 mm. Hg 15

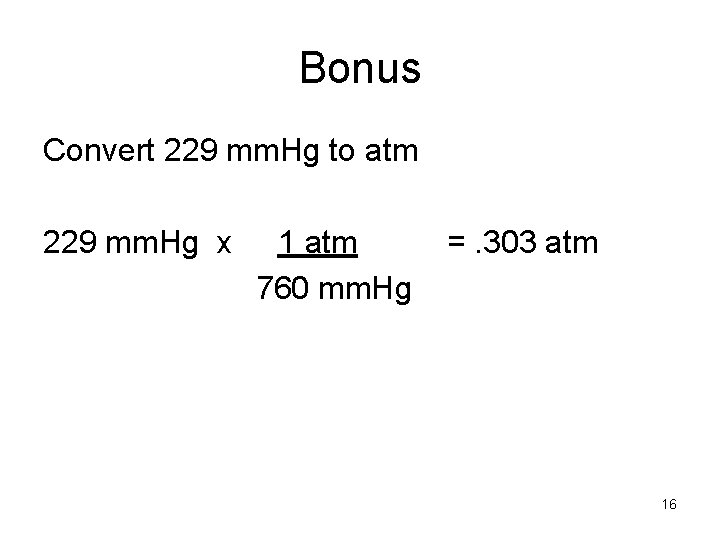
Bonus Convert 229 mm. Hg to atm 229 mm. Hg x 1 atm 760 mm. Hg =. 303 atm 16

Charlies' Law Demo • By warming the balloon up, we increase the speed of the moving gas molecules inside it. • This increases the rate at which the gas molecules hit the wall of the balloon. • Because the balloon’s skin is elastic, it expands upon this increased pushing from inside, and the volume taken up by the same mass of gas increases with temperature. 17

Charlie’s Law • At constant pressure the volume of gas is direct proportional to its temperature. Note: Temp is ALWAYS in V 1 = V 2 Kelvin!!!! T 1 T 2 T↓ T↑ V↓ V↑ 18

Charles's Law Mini Lab 19

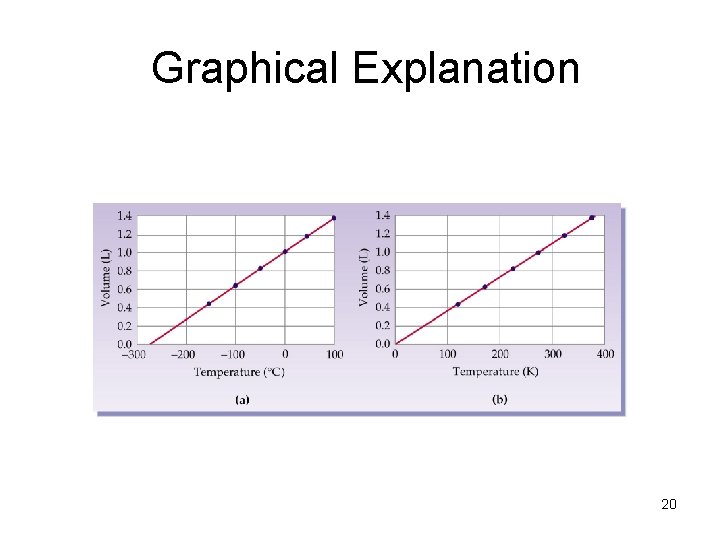
Graphical Explanation 20

Charles's Law Example A balloon is filled to a volume of 7. 00 x 102 ml at a temperature of 20. ◦C. The balloon is then cooled at a constant pressure to a temperature of 1. 0 x 102 K. What is the final volume of the balloon? 21

Answer 20 C + 273 = 293 K 7. 00 x 102 ml = V 2 293 K 1. 0 x 102 K. V 2= 238. 9 ml 22

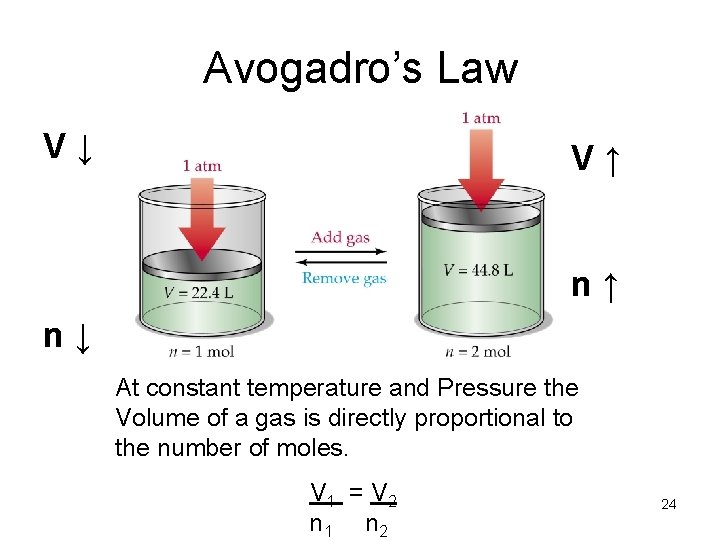
Avogadro’s Law • Equal volumes of gas at the same temperature and pressure contain equal numbers of moles. • If temperature and Pressure are constant Volume of a gas is directly proportional to the number of moles. 23

Avogadro’s Law V↓ V↑ n↑ n↓ At constant temperature and Pressure the Volume of a gas is directly proportional to the number of moles. V 1 = V 2 n 1 n 2 24

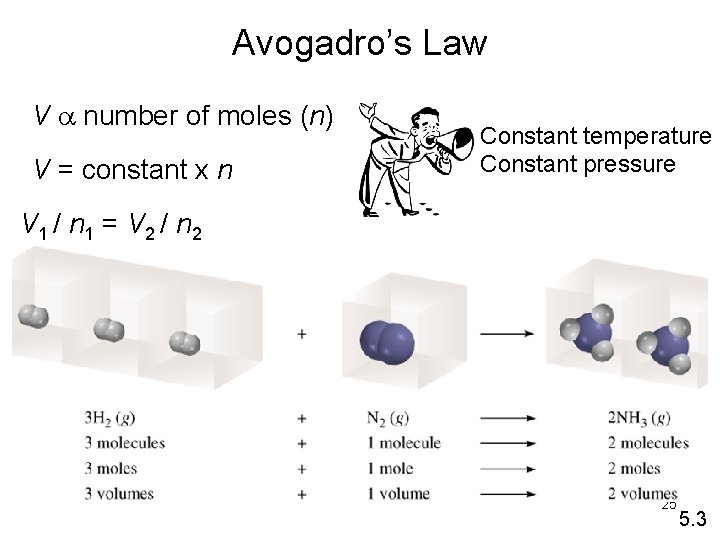
Avogadro’s Law V a number of moles (n) V = constant x n Constant temperature Constant pressure V 1 / n 1 = V 2 / n 2 25 5. 3

Example • How many liters of O 2 gas are required to prepare 100 L of CO 2 gas by the following reaction. 2 CO (g) + O 2 (g) 2 CO 2 (g) 26

Answer V 1 = V 2 n 1 n 2 100 = V 2 2 1 V 2= 50 L 27

Homework Chang: pg 210 -211 #”S : 13, 15, 18, 19, 21, 23 BL 3, 17, 19, 20, 21 28

Combined Gas Law • This is used when nothing is constant in an experiment. P 1 V 1 T 1 = P 2 V 2 T 2 29

Example A gas is contained in a cylinder with a temperature of 281 K and a volume of 2. 1 ml at a pressure of 6. 4 atm. The gas is heated to a new temperature of 298 K and the pressure decreases to 1 atm. What is the new volume of the gas. 30

Answer P 1 V 1 T 1 P 1= 6. 4 atm V 1 = 2. 1 ml T 1 = 281 k P 2= 1 atm V 2= ? T 2 = 298 K = P 2 V 2 T 2 6. 4 (2. 1) = 1 (V 2) 281 298 V 2 = 14 ml 31

Ideal Gas Law 10. 4 Ideal gas: a hypothetical gas whose pressure (atm), volume (L), and temperature (K) behave as predicted every time. (Perfect like each and everyone of you!) One can visualize it as a collection of perfectly hard spheres which collide but which otherwise do not interact with each other. Ideal Gas Law: PV = n. RT gas constant: R= 0. 0821 L x Atm/mol x K 32

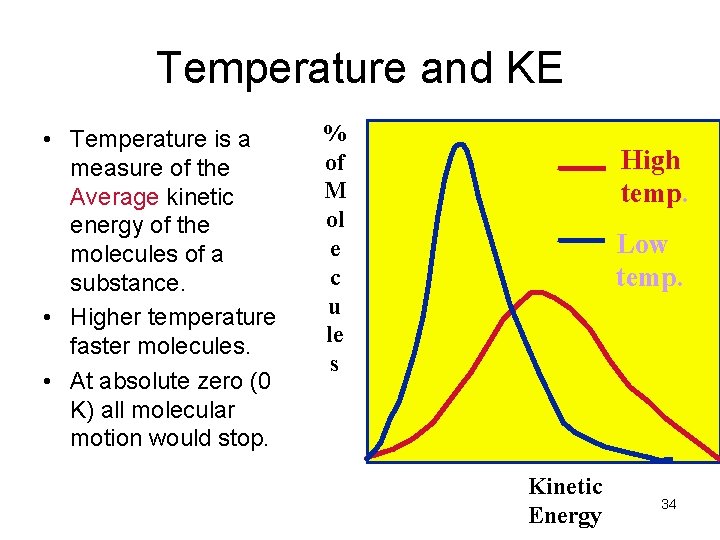
Temperature and KE • Temperature is a measure of the Average kinetic energy of the molecules of a substance. • Higher temperature faster molecules. • At absolute zero (0 K) all molecular motion would stop. % of M ol e c u le s High temp. Low temp. Kinetic Energy 34

Kinetic Molecular Theory • The Kinetic Molecular Theory explains the forces between molecules and the energy that they possess. This theory has 3 basic assumptions. 35

KMT 1. Matter is composed of small particles (molecules). The measure of space that the molecules occupy (volume) is derived from the space in between the molecules and not the space the molecules contain themselves. 36

• The molecules are in constant motion. This motion is different for the 3 states of matter. Solid - Molecules are held close to each other by their attractions of charge. They will bend and/or vibrate, but will stay in close proximity. Liquid - Molecules will flow or glide over one another, but stay toward the bottom of the container. Motion is a bit more random than that of a solid. Gas - Molecules are in continual straightline motion. The kinetic energy of the molecule is greater than the attractive force between them, thus they are much farther apart and move freely of each other. 37

KMT 3 • When the molecules collide with each other, or with the walls of a container, there is no loss of energy. • Random Fact: The Average speed of an oxygen molecule is 1656 km/hr at 20ºC 38

Example • A 50. 0 L cylinder of acetylene C 2 H 2 has a pressure of 17. 1 atm at 21 C. What is the mass of acetylene in the cylinder. 39

Answer PV = n. RT 21 + 273 = 294 K 17. 1 (50. 0) = n (0. 0821) (294) n = 35. 4 mol Need answer in grams • 35. 4 C 2 H 2 x 26 g C 2 H 2 = 920 g C 2 H 2 1 mol C 2 H 2 40

A short Way to do that • mw = m. RT = d. RT PV P An unknown gas weighs 34 g and occupies 6. 7 L at a pressure of 2 atm at temperature of 245 K. What is its average molecular weight. 41

Answer • 51 g/mol 42
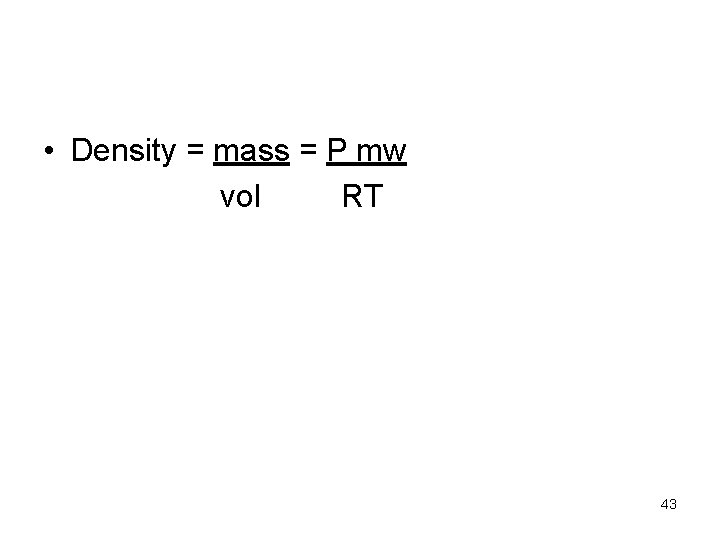
• Density = mass = P mw vol RT 43

STP • Standard Temperature and Pressure • P = 1 atm = 760 torr • T = 273 K • Molar volume of ideal gas at STP = 22. 42 L 44

What is the volume (in liters) occupied by 49. 8 g of HCl at STP? 0 C = 273. 15 K T = 0 Given: PV = n. RT V= P P = 1 atm n = 49. 8 g x 1. 37 mol x 0. 0821 V= L • atm mol • K 1 mol HCl = 1. 37 mol 36. 45 g HCl x 273. 15 K 1 atm V = 30. 6 L 45 5. 4

Argon is an inert gas used in lightbulbs to retard the vaporization of the filament. A certain lightbulb containing argon at 1. 20 atm and 18 0 C is heated to 85 0 C at constant volume. What is the final pressure of argon in the lightbulb (in atm)? PV = n. RT n, V and R are constant n. R = P = constant T V P 1 P 2 = T 1 T 2 P 1 = 1. 20 atm T 1 = 291 K P 2 = ? T 2 = 358 K T 2 = 1. 20 atm x 358 K = 1. 48 atm P 2 = P 1 x 291 K T 1 46 5. 4

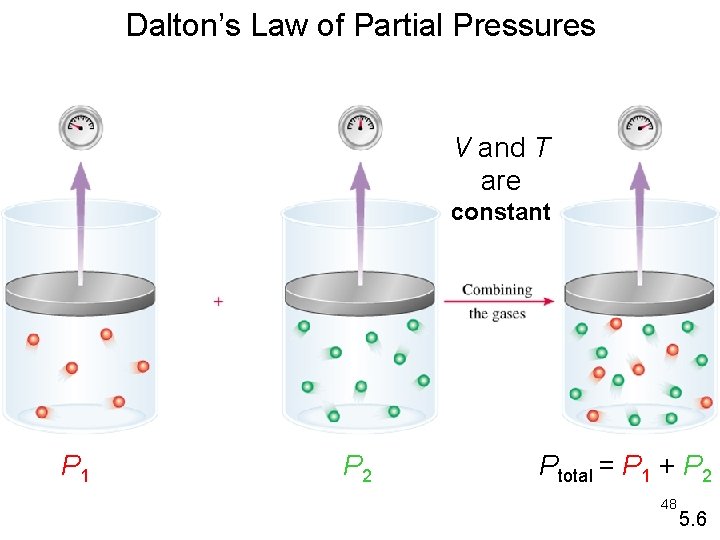
Dalton’s Law of Partial Pressure • The sum of the partial pressures of the system is equal to the total pressure of the system. • Ptotal = P 1 + P 2 + P 3 47

Dalton’s Law of Partial Pressures V and T are constant P 1 P 2 Ptotal = P 1 + P 2 48 5. 6

Homework Chang pg 211 DAY 1 #’s 27, 29, 31, 33 Day 2 #’s 38, 41, 49, 51 -53, 62, 66, 71 Write out the combined gas law and ideal gas law formula 5 times each and then do problems 23, 27, 28, 38 49