Gas Dynamics ESA 341 Chapter 2 Dr Kamarul

Isentropic Flow n n n Introduction Derivation Stagnation properties IF in a converging and

Introduction Consider a gas in horizontal sealed cylinder with a piston at one end.

Introduction Examples of isentropic flows: Jet or rocket nozzles, diffusers. Airfoils. Isentropic core flow

Derivation For isentropic flow: And: So: Applying energy eqn to get relation between T

Derivation To find relation between A & M: Using relation -M and T-M Where:

Stagnation Properties Stagnation condition is a condition that would exist if the flow at

Stagnation Properties Examples 2 0 1 Stagnation point is point 0. Stagnation point is

Isentropic Relations in Tabular Form – Appendix B: Example: M T 0/T 0. 50

Pitot Probe Measurement for Compressible Flow: V=0 P Incompressible flow (Bernoulli eqn): Compressible flow:

Critical Conditions: Critical condition is a condition that would exist if the flow was

Group exercises 2 1. Calculate the Mach number of two aircraft both travelling with

Slides: 13

Download presentation

Gas Dynamics ESA 341 Chapter 2 Dr Kamarul Arifin B. Ahmad PPK Aeroangkasa

Isentropic Flow n n n Introduction Derivation Stagnation properties IF in a converging and converging-diverging nozzle Application

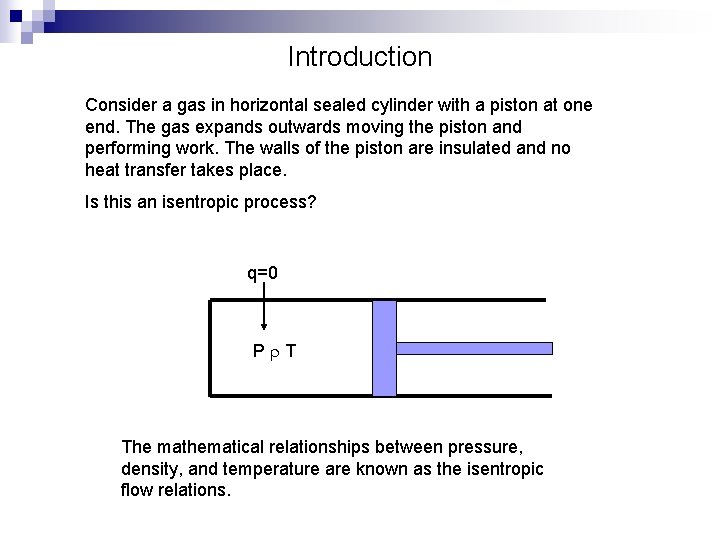
Introduction Consider a gas in horizontal sealed cylinder with a piston at one end. The gas expands outwards moving the piston and performing work. The walls of the piston are insulated and no heat transfer takes place. Is this an isentropic process? q=0 P T The mathematical relationships between pressure, density, and temperature are known as the isentropic flow relations.

Introduction Examples of isentropic flows: Jet or rocket nozzles, diffusers. Airfoils. Isentropic core flow But in reality there is no real flow is entirely isentropic!!

Derivation For isentropic flow: And: So: Applying energy eqn to get relation between T & M:

Derivation But: And: So: cont.

Derivation To find relation between A & M: Using relation -M and T-M Where: cont.

Stagnation Properties Stagnation condition is a condition that would exist if the flow at any point was isentropically brought to or come from rest (V =M= 0). Stagnation values:

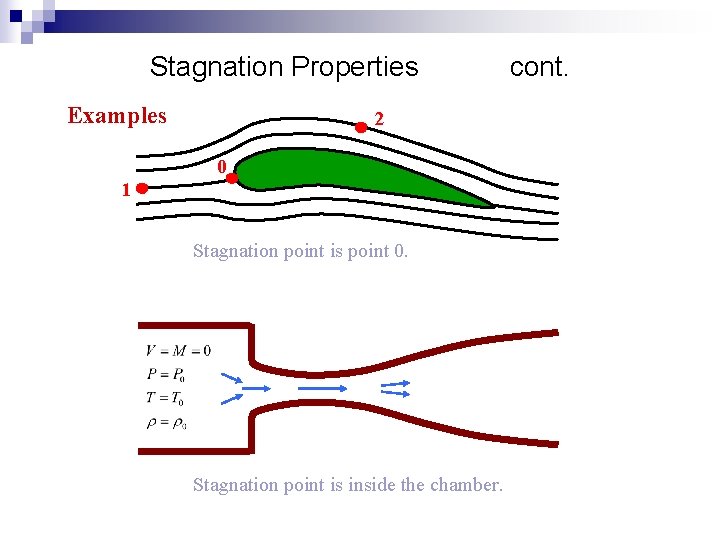
Stagnation Properties Examples 2 0 1 Stagnation point is point 0. Stagnation point is inside the chamber. cont.

Isentropic Relations in Tabular Form – Appendix B: Example: M T 0/T 0. 50 P 0/P 0/ a 0/a A/A* q 1. 05000 1. 18621 1. 12973 1. 02470 1. 33984 2. 15200 17. 08589 7. 59373 1. 50000 2. 63671 2. 40 36. 74650

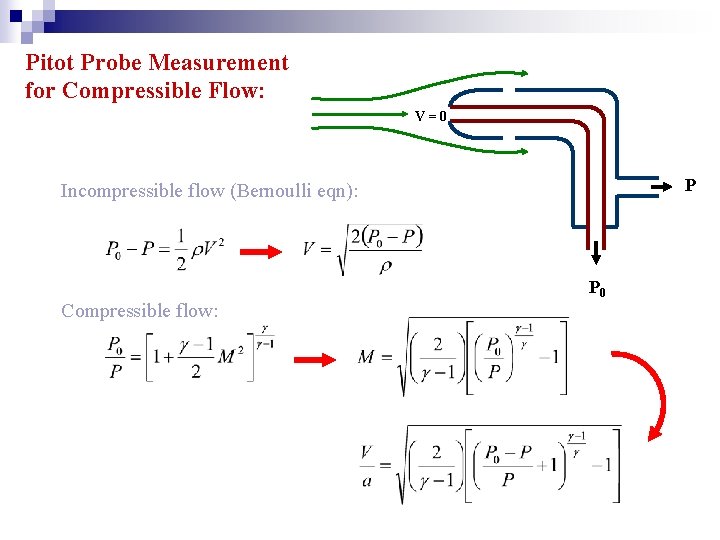
Pitot Probe Measurement for Compressible Flow: V=0 P Incompressible flow (Bernoulli eqn): Compressible flow: P 0

Critical Conditions: Critical condition is a condition that would exist if the flow was isentropically accelerated or decelerated until M = 1. M*=1 T*, P*, r*, A*, a* = 5 A/A* 1 Mach number 2 3 4 M<1 M>1 A=A* M=1

Group exercises 2 1. Calculate the Mach number of two aircraft both travelling with an airspeed of 300 m/s. One is traveling at sea level (T=250 C); the other at an altitude of 11 km (T=-160 C. ) 2. A perfect gas with is traveling at Mach 3 with a static temperature of 250 K, a static pressure of 101 k. Pa, and a static density of 1. 4077 kg/m 3. Determine the stagnation temperature, pressure, and density values. 3. An aircraft is flying at 80 m/s at sea level where the temperature is 200 C, density is 1. 225 kg/m 3 and pressure is 1030. 1 mbar. Assuming R=287 J/kg. K what Mach number is the aircraft flying? Air stagnates near the leading edge. Assuming isentropic compressible flow calculate the stagnation pressure. Assuming incompressible flow, use Bernoulli’s equation to calculate the stagnation pressure. What is the error in assuming incompressible flow at this Mach number?