Gap Rounding and Integer Decomposition I general Andrs

Gap, Rounding and Integer Decomposition I general András Sebő, CNRS (G-SCOP) Grenoble

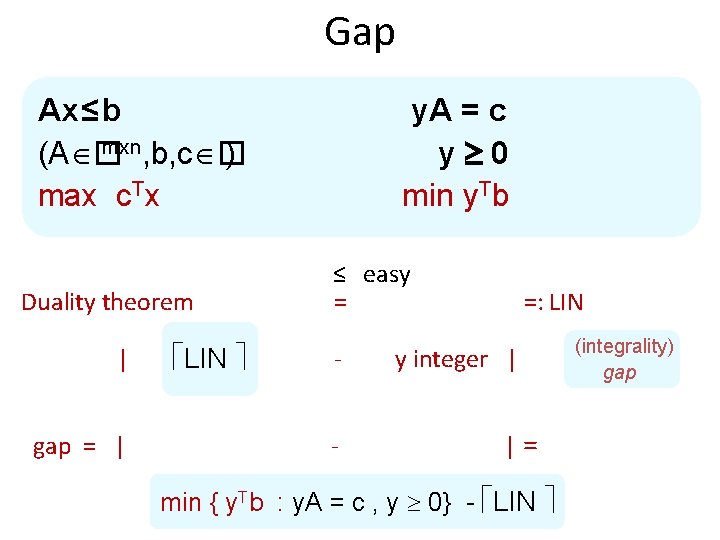
Gap Ax ≤ b mxn, b, c � (A � ) max c. Tx y. A = c y 0 min y. Tb ≤ easy Duality theorem =: LIN duality (integrality) | x integer - y integer | LIN gapgap gap = | - | = min { y. Tb : y. A = c , y 0} - LIN

Your future Gap=0: illustrated definitions, related notions Examples: TU and generalizations, matroids, … cyclic interval matrices general stable sets in special graphs special stable sets in general graphs bin packing Properties: adding columns, projection, applications Gap=1: bins, matchings, common indep. of 2 matroids Algorithmic and other uses

gap = 0 : Integer Rounding (IR) Ax ≤ b mxn, b, c � n) (A � max c. Tx y. A = c y 0 min y. Tb ≤ easy Duality theorem =: LIN(c) The system Ax ≤ b – or (A, b) – integer rounding, if c : {min y. Tb, y. A = c, y 0, y integer } = LIN(c)

Nothing to round : TDI The system Ax ≤ b – or (A, b) – integer rounding, if n : {min y. Tb, y. A = c, y 0, y integer}= LIN(c) c � The system Ax ≤ b totally dual integral (TDI), if n : {min y. Tb, y. A = c, y 0, y integer} = LIN(c) c � So: integer rounding & LIN(c) is integer c = TDI system = IR system & integer polyhedron

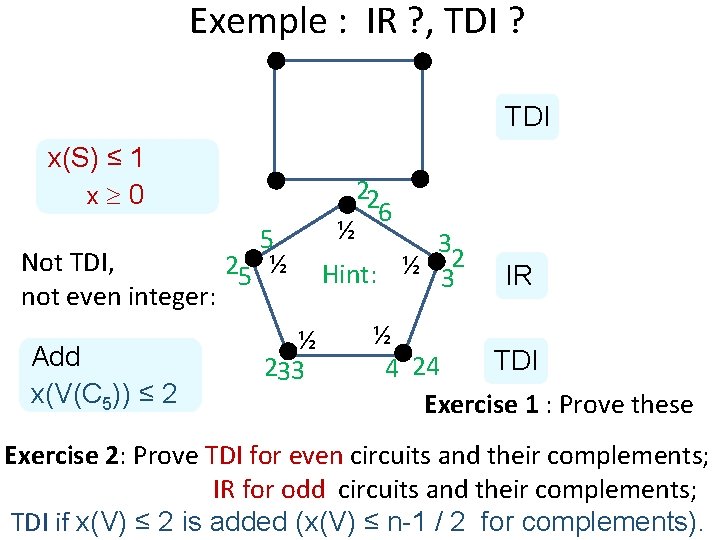
Exemple : IR ? , TDI ? TDI x(S) ≤ 1 x 0 Not TDI, not even integer: Add x(V(C 5)) ≤ 2 5 25 ½ ½ 22 6 3 2 ½ Hint: 3 IR ½ TDI 4 24 Exercise 1 : Prove these Exercise 2: Prove TDI for even circuits and their complements; IR for odd circuits and their complements; TDI if x(V) ≤ 2 is added (x(V) ≤ n-1 / 2 for complements). ½ 233

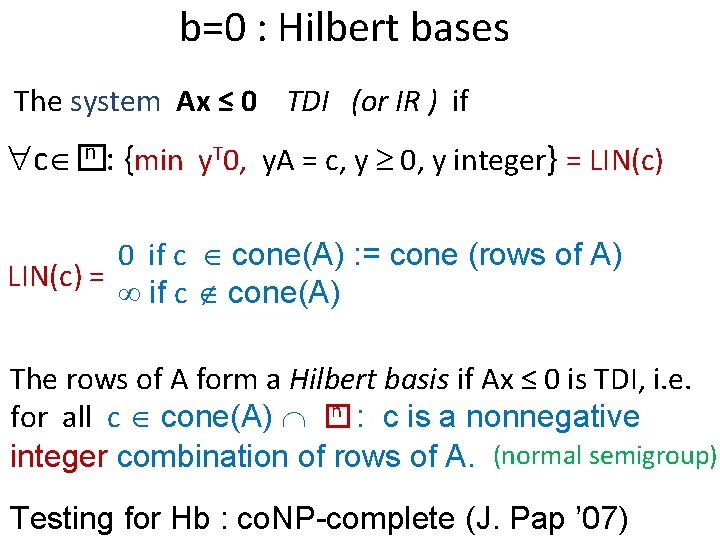
b=0 : Hilbert bases The system Ax ≤ 0 TDI (or IR ) if n : {min y. T 0, y. A = c, y 0, y integer} = LIN(c) c � 0 if c cone(A) : = cone (rows of A) LIN(c) = if c cone(A) The rows of A form a Hilbert basis if Ax ≤ 0 is TDI, i. e. n : c is a nonnegative for all c cone(A) � integer combination of rows of A. (normal semigroup) Testing for Hb : co. NP-complete (J. Pap ’ 07)

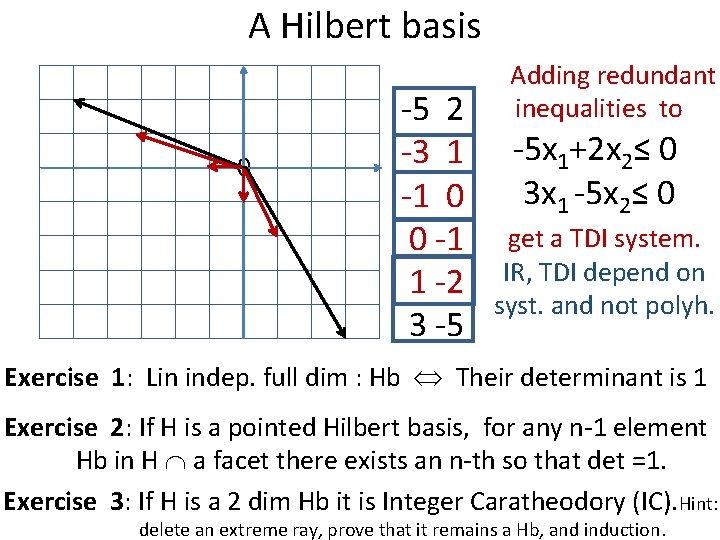
A Hilbert basis Adding redundant inequalities to 0 -5 2 -5 x 1+2 x 2≤ 0 -3 1 3 x 1 -5 x 2≤ 0 -1 0 0 -1 get a TDI system. 1 -2 IR, TDI depend on syst. and not polyh. 3 -5 Exercise 1: Lin indep. full dim : Hb Their determinant is 1 Exercise 2: If H is a pointed Hilbert basis, for any n-1 element Hb in H a facet there exists an n-th so that det =1. Exercise 3: If H is a 2 dim Hb it is Integer Caratheodory (IC). Hint: delete an extreme ray, prove that it remains a Hb, and induction.

Results & problems on Integer Caratheodory Thm: (S. ‘ 90) If n=3, Integer Caratheodory property is true Thm: (Bruns, Gubeladze ‘ 98) Not true in 6 dim Problem: Integer Caratheodory number of Hilbert cones Thm: (Gijswijt 2010) True for matroid bases. Problem: For rooted arborescences ? Exercise: (CFS‘ 86) True for optimal w-coloring in perfect graphs in particular maximum stable-sets form a `Caratheodory Hb’. Thms: (Eisenbrand, Shmonin 2005) Caratheodory bounds without the Hilbert (or ID) property, for integer cones

IR & Hb The system Ax ≤ b – or (A, b) – IR, if c : {min y. Tb, y. A = c, y 0, y integer } = LIN(c) n Hb if h cone(H) � n : H � h is a nonnegative integer combination of rows of A. A, b Thm: (Giles, Orlin 1981) IR rows of form a Hb. 0, 1

Integer Decomposition (ID) n has the ID property, if Set of integer vectors P � n & k � v k conv(P) � v= v 1 + … + vk , v 1 , … , vn P Matrix A is ID if the row-set of A is so. Fact: P=set of all integer points of the convex hull P of integer points ; if P is a polyhedron, it is integer. n is ID Def: A polyhedron P is ID iff P is integer and P � n & k � n v k. P � v= v 1 + … + vk, v 1 , …, vn P �

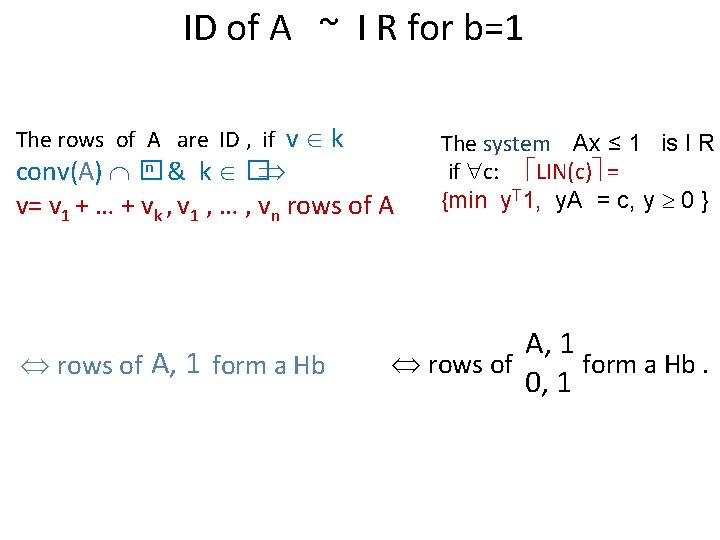
ID of A ~ I R for b=1 The rows of A are ID , if v k n & k � conv(A) � v= v 1 + … + vk , v 1 , … , vn rows of A A, 1 rows of form a Hb The system Ax ≤ 1 is I R if c: LIN(c) = {min y. T 1, y. A = c, y 0 } A, 1 rows of form a Hb. 0, 1

I R for b=1 or 0 ~ ID of extended A The system Ax ≤ 1, Bx ≤ 0 integer rounding, if c: {min y. T 1, y. A+z. B = c, y, z 0, y, z integer } = LIN(c) A, 1 rows of form a Hb. B, 0 (if (0, 1) is in the intcone of the rest) 0, 1 Useful example : B = -Id, and A has a non-neg row. Then (0, 1) is in the integer cone of the other rows.

mxn , x 0, b=1 : IR ID A � + mxn, c �n ) Ax ≤ 1 (A � + + x 0 max c. Tx y. A c y 0 min y. T 1 Assume: rows of A contain every integer vector in the ‘downhull’ of their convex (inessential if 0 -1) hull. min y. T 1, y. A c, y integer = LIN(c) n can be written as c=a + … + a c k conv (A) � 1 k

mxn , x 0, b=-1 : IR ID A � mxn, c �n ) Ax ≥ 1 (A � + + x 0 min c. Tx y. A ≤ c y 0 max y. T 1 Imagine: rows of A contain every integer vector in the ‘uphull’ of their convex (inessential if 0 -1) hull. max y. T 1, y. A ≤ c, y integer = LIN(c) n can be written as c=a + … + a c k conv (A) � 1 k

The assumption always holds for us Ax ≤ 1 x 0 Assume: rows of A contain every integer vector in the ‘downhull’ of their convex (inessential if 0 -1) hull. Ax ≥ 1 x 0 Imagine: rows of A contain every integer vector in the ‘uphull’ of their convex (inessential if 0 -1) hull. +k +1 Integer Rounding of the systems = MIR MID Integer Decomposition of the rows of A. +1 +k Direct check in a glance: MID = MIR (enough to check IR for LIN � )

Examples : not ID and ID not ID: Loose examples for ID: matchings in bipartite graphs, consec 1 polyhedra , stable sets in perfect graphs, (uphull of) rooted arborescences in digraphs, … TDI Relevant examples for ID: matchings in special graphs, (common) indep in (spec) matroids, TU polyhedra, IR circular intervals, cyclic stable sets, bin patterns, …

Gap, Rounding and Integer Decomposition II. nonnegative matrices, nonnegativity constraints András Sebő, CNRS (G-SCOP) Grenoble

IR , ID The system Ax ≤ b is IR, if c: {min y. Tb, y. A = c, y 0, y integer } = LIN(c) Def: A polyhedron P is ID, if k � , n v= v + … + v , …, v P � n v k. P � 1 k We will also say that the integer points of P have ID. n A � + Ax ≤ 1 Ax ≥ 1 x 0 If A itself is the set of integer points of a hereditary integer polyhedron P , the two are the same.

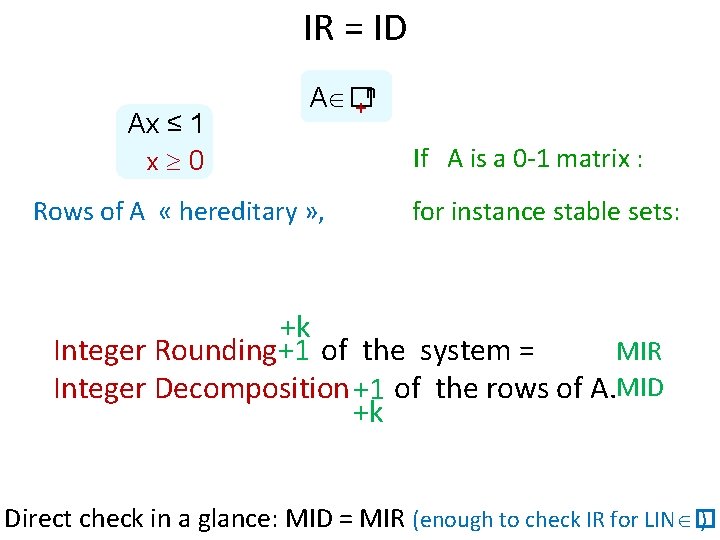
IR = ID Ax ≤ 1 x 0 n A � + Rows of A « hereditary » , If A is a 0 -1 matrix : for instance stable sets: +k +1 Integer Rounding of the system = MIR MID Integer Decomposition of the rows of A. +1 +k Direct check in a glance: MID = MIR (enough to check IR for LIN � )

Examples : not ID and ID not ID: Loose examples for ID: matchings in bipartite graphs, consec 1 polyhedra , stable sets in perfect graphs, (uphull of) rooted arborescences in digraphs, … TDI Relevant examples for ID: matchings in special graphs, (common) indep in (spec) matroids, TU polyhedra, IR circular intervals, cyclic stable sets, bin patterns, …

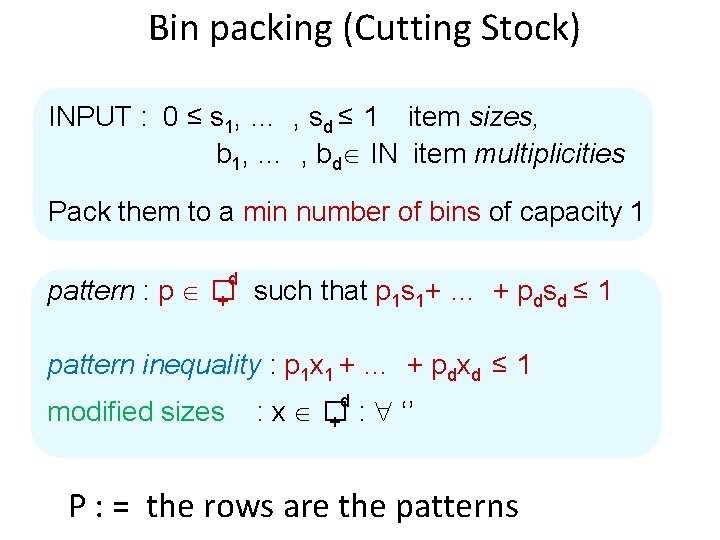
Bin packing (Cutting Stock) INPUT : 0 ≤ s 1, … , sd ≤ 1 item sizes, b 1, … , bd IN item multiplicities Pack them to a min number of bins of capacity 1 d pattern : p � + such that p 1 s 1+ … + pdsd ≤ 1 pattern inequality : p 1 x 1 + … + pdxd ≤ 1 d modified sizes : x � + : ‘’ P : = the rows are the patterns

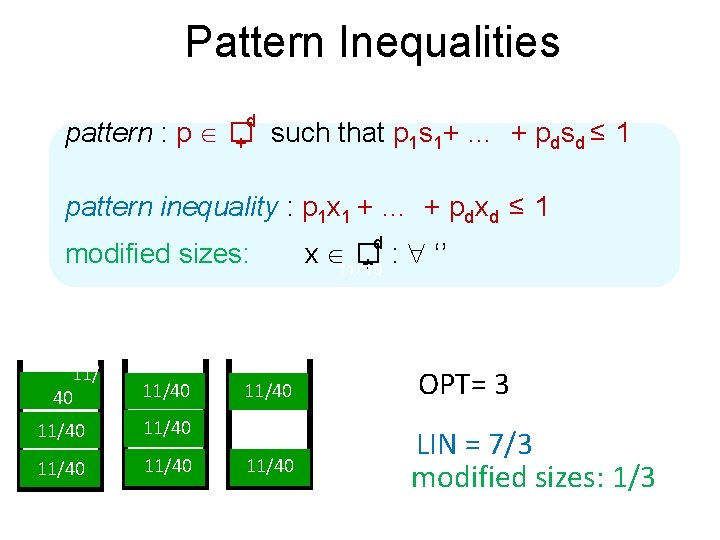
Pattern Inequalities 1/3 d pattern : p � + such that p 1 s 1+ … + pdsd ≤ 1 pattern inequality : p 1 x 1 + … + pdxd ≤ 1 d modified sizes: x � + : ‘’ 11/40 11/40 11/40 11/40 OPT= 3 LIN = 7/3 modified sizes: 1/3

Pattern Inequalities d pattern : p � 1/3 + such that p 1 s 1+ … + pdsd ≤ 1 pattern inequality : p 1 x 1 + … + pdxd ≤ 1 d modified sizes : x � + : ‘’ Gilmore-Gomory LP of all « pattern inequalities » : big x d Px ≤ 1 (P � ) + x 0 d T max b x (b � + ) Max of total modified size y. P b y 0 = min y. T 1 Bin packing

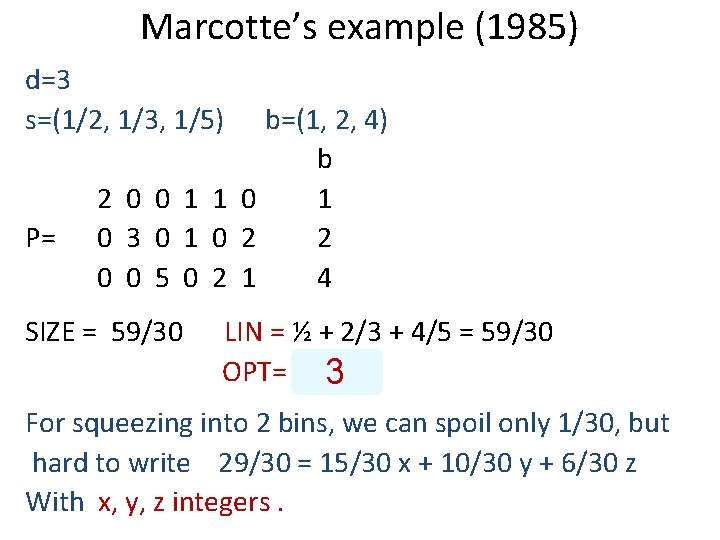
Marcotte’s example (1985) d=3 s=(1/2, 1/3, 1/5) b=(1, 2, 4) b 2 0 0 1 1 0 1 P= 0 3 0 1 0 2 2 0 0 5 0 2 1 4 SIZE = 59/30 LIN = ½ + 2/3 + 4/5 = 59/30 OPT= 2 or 3 ? 3 For squeezing into 2 bins, we can spoil only 1/30, but hard to write 29/30 = 15/30 x + 10/30 y + 6/30 z With x, y, z integers.

d=2 : Mc. Cormick, Smallwood, Spieksma big x 2 P � + 2 : b � + y. P = b y 0 min y. T 1 d pattern : p � + such that p 1 s 1+ … + pdsd ≤ 1 Thm: {(p, 1): p P} is a Hb Proof: Any 3 lin indep forming a lifted simplex is a Hb (i. e. is unimodular). Cor: P is ID ; pol. alg.

Stable sets I : matchings M (G): =conv(matchings of G) PM(G): =conv (perfect m. ). Thm (König ) G bipartite : they are ID. Conjecture (Lovász ) : G without Petersen minor : they are ID Conjecture (Goldberg, Seymour ) : MID = ID +1 x k M (G) x = M 1 + … + Mk+1 Exercise : Determine cone (M(G), 1). Prove the ‘fractional Vizing theorem’. (Odd sets disappear, why ? )

Stable sets that are ID Problem : Characterize graphs whose stable sets are ID Difficult, but : Are h-perfect (t-perfect) graphs among them ?

Independent sets of matroids (Edmonds) mxn, c �n) Ax ≤ 1 (A � + + x 0 max c. Tx y. A c y 0 min y. T 1 M= (S, F ) matroid, rows of A: { I {0, 1}S: I independent} A is integer rounding so integer decomposition, and : S : k conv( A ) = {x � x(U) ≤ k r(U) U S} box-TDI that is, has an integer solution adding upper bounds

ID + k box TDI M= (S , F ) matroid x(U) ≤ k r(U) U S xi ≤ 1 i S Theorem (variant of Edmonds’ matroid partition) max union of k independent sets = min {|X| + k r(S X) : X S } Conjecture (Aharoni) : Matroid intersection is MID

List coloring Theorems Theorem (Galvin): G bipartite. If it can be k-edge-colored, Then it can also be list-edge-colored if the lists are ≥ k. Exercise: M=(S, F) matroid. If it is the union of k indep sets then it can be also list-independent colored if the lists are ≥ k. (Seymour) Hint: Define matroid M 1, … , Mk on the sets Si : = {e S: e has colour i in its list}. Check the condition of the matroid partition theorem using that S can be covered by k independent sets of M.

TU polyhedra are ID Theorem (Baum and Trotter 1977) n : Ax b} is ID A is TU Q: ={x � Proof : Let xk k. Q. We are looking for x � : (i) x Q , (ii) xk - x (k-1) Q Exercise : Check that for fixed xk both (i) and (ii) are linear systems with matrix A, and altogether x has a unimodular coeff matrix. Note that (i), (ii) is feasible : xk/k is a feasible solution. So, since x has a unimod coeff matrix an integer solution exists and can be computed.

The projection project Is the projection of ID polyhedra ID ? If YES, then new examples ! If NO, then is it true for TU ? Applications ?

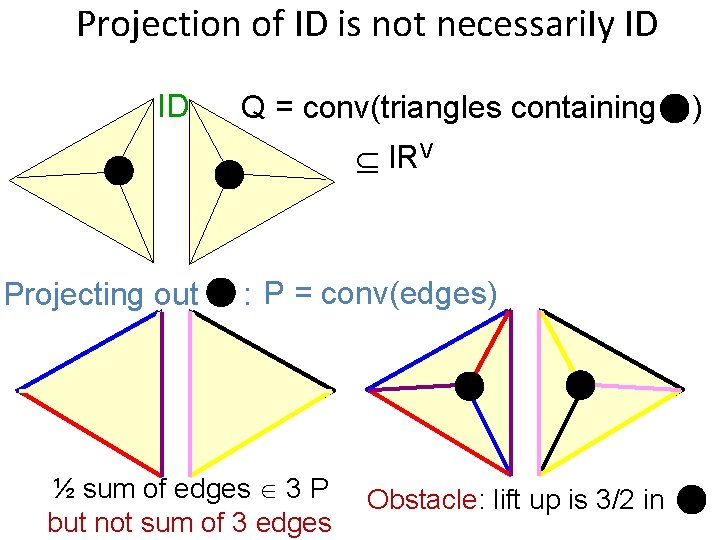
Projection of ID is not necessari. Iy ID ID Q = conv(triangles containing ) IRV Projecting out : P = conv(edges) ½ sum of edges 3 P but not sum of 3 edges Obstacle: lift up is 3/2 in

Projection Proposition : If A is TU, then projections of Q: = {x : Ax b} are ID. (S. 2008) Proof : Q Zn’, let n < n’ and P: = {(y 1, … , yn ) : y Q } Let z k. P , z integer. z/k P , so z’: (z/k, z’) Q , i. e. (z, kz’) k. Q kz’ is a solution of A’x’ b’ (= kb – z. A(. ; 1, . . . , n)) So kz’ can be chosen to be integer. DONE

Chains, antichains in posets Dilworth theorem (1950): max stable set (antichain) = min { |P| : P partition into paths } Greene-Kleitman theorem (1976): max union of k stable sets (antichain), =min {|X| + k|P| : X V, P set of disj paths (chains) X = vertices uncovered by P}

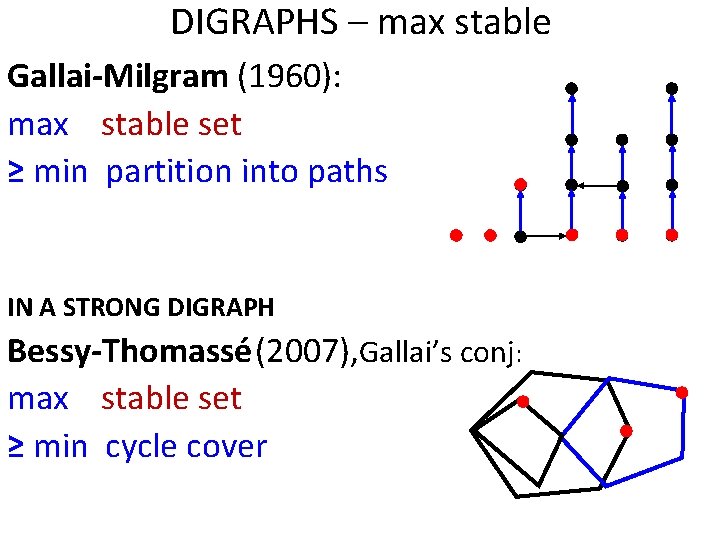
DIGRAPHS – max stable Gallai-Milgram (1960): max stable set ≥ min partition into paths IN A STRONG DIGRAPH Bessy-Thomassé (2007), Gallai’s conj: max stable set ≥ min cycle cover

DIGRAPHS – max k- colored subgraphs Berge-Linial conjecture (1981): Schrijver, Prob 5 max union of k stable sets ≥ min {|X| + k|P| : X V, P set of disj paths, X uncovered } Strongly connected version: max union of k stable sets ≥ min {|X| + k|C| : X V, C set of circuits, X uncovered} (Whose conjecture ? )

Stable sets in graphs II : cyclic stable sets From ID + k box TDI for cyclic stable sets : Theorem (S. 2007) G strongly connected max union of k stable sets ≥ min {|X| + k|C| : C set of circuits X = vertices uncovered by C }

Connexions ? : IR of cyclic sets Applications of the projection : minmax – IR property- for particular (cyclic) stable sets (S: JCT/B 2007) and their relation to path partitions in arbitrary or to cyclecovers in strongly connected graphs. (S: Survey Ref 4. ) Nearly unimodular: add a row of a unimodular matrix to the others. Application cyclic interval constraints. (Gijswijt 2005: Ref 3. ) Maximum stable sets in (fuzzy) circular interval graphs (3 organizers and a would-be participant) Multiflows in rings (Cedric Bentz thesis, 2006)

Nearly unimodular matrices U unimodular, U � mxn, u � n. M= U + C, where the rows Def : u. T of C are integer multiples of u : nearly unimodular (NU) n: Mx≤b} is ID. Thm(Gijswijt) Let M NU: PM, b: = {x � Proof: PM, b, s : = PM, b {x : u. Tx = s} is ID ( Baum, Trotter) Claim: PM, b {q ≤ u. Tx ≤ q+1} is ID q � . q+1 q x n. u. T(kx)=qk + r, 0 < r < q Let x ’’, kx � Then x= y + (1 - )z , y PM, b, q+1 , z PM, b, q kx= k y + (k- k )z , y PM, b, q+1 , z PM, b, q k =r

kx= ry + (k- r)z , y PM, b, q+1 , z PM, b, q n fixed, y’ , z’ CBC � n : x’ y’ z’ : x’ � y’ r PM, b, q+1 , x’ - y’ (k-r) PM, b, q+1 unimodular system for y’. Q. E. D. Problem: Other operations getting to new ID systems ?

Conclusion IR (with integral vetices: TDI) the same as ID for nonneg matrices, nonnegativity constraints : ID Classical examples, operations, « Cyclic combinatorial objects » Pol alg : direct comb algs or ellipsoids if A explicitly given MID (ID +1): Matching, matroid intersection and Bin packing (comb approach, general Lemmas, consequence for 7 sizes)

BONUS : BACK TO BINS m: =LIN = integer (ID=IR)

Critical instances Start of proof: b-lexicographically minimal counterexample to what ? We call an instance I critical , if for any pattern P : LIN (I P) > LIN (P) – 1 Another kind of minimality : If we decrease b lexicographically, one less bin is enough. NFD order quite good, but simplest proofs from : m+2 th bin lex min, then m+1 th bin lex min, …:

OPT= m+2 In the last bin: only the smallest item s.

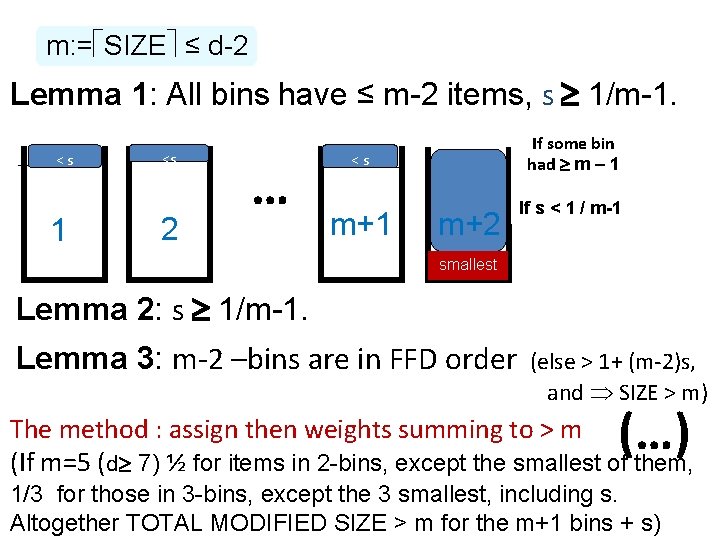
m: = SIZE ≤ d-2 Lemma 1: All bins have ≤ m-2 items, s 1/m-1. < s 1 <s 2 … < s m+1 < s m+2 smallest If some bin had m – 1 If s < 1 / m-1 Lemma 2: s 1/m-1. Lemma 3: m-2 –bins are in FFD order (else > 1+ (m-2)s, and SIZE > m) (…) The method : assign then weights summing to > m (If m=5 (d 7) ½ for items in 2 -bins, except the smallest of them, 1/3 for those in 3 -bins, except the 3 smallest, including s. Altogether TOTAL MODIFIED SIZE > m for the m+1 bins + s)

GAP ≠ 0 for bin packing m x d Px ≤ 1 (P � ) + x 0 d max b. Tx (b � + ) y. P b y 0 = min y. Tb 2 i 2 i + 2 i 2 j Marcotte (1985) , Rizzi (1997) : gap≠ 0 Scheithauer & Terno’s(1997) conjecture : gap=1 ‘MIRUP’ (Modified integer rounding property) , proved for d ≤ 6 Shmonin, S. (2006 - …) Combinatorial properties of critical instances, implies MIRUP for d ≤ 7, simpler for Karmarkar, Karp (’ 82) additive error log 2 d (AFPTAS)

Results on cutting stock LIN : ~ P ellipsoid method; knapsack separation d= 2 : P Mc. Cormick, Smallwood, Spieksma (’ 93) d = fix : OPT +1 P Jansen, Solis-Oba, (‘ 10) d=fix not necessary : If GAP ≤ 1, then OPT ≤ LIN +1 always, and LIN+1 P AFPTAS : Karmarkar, Karp additive error log 2 d (’ 82) These and Marcotte’s examples support ‘MIRUP’’ (Modified integer rounding property) , stated by Scheithauer Terno (1997) : gap=1

Results on MIRUP d=2 & : Mc. Cormick, Smallwood, Spieksma (’ 93) d=3, 4, 5, 6 : MIRUP Scheithauer and Terno (’ 97) Towards a critical combinatorial structure implying : d 7: MIRUP with polynomial algorithm (Shmonin, S. ’ 06) General combinatorial lemmas Structure when all bins are of size at most 3. All sizes > 1/4 (Eisenbrand, Pálvölgyi, Rothvoss 2010: constant gap reduced to (specialized ? Generally false) conjecture of Beck. )

Questions on bin packing For d = 3 P ? For d = 8 GAP = 1 ? 3 – partition ? ~ All sizes > ¼ Relations between GAP=1 problems OPT+1 ? Fix dim P by Jansen, Solis-Oba, (‘ 10)