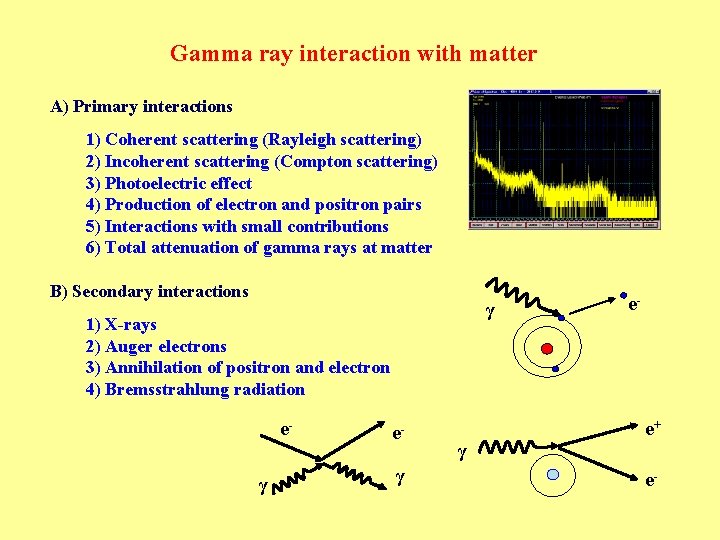
Gamma ray interaction with matter A Primary interactions

Gamma ray interaction with matter A) Primary interactions 1) Coherent scattering (Rayleigh scattering) 2) Incoherent scattering (Compton scattering) 3) Photoelectric effect 4) Production of electron and positron pairs 5) Interactions with small contributions 6) Total attenuation of gamma rays at matter B) Secondary interactions γ 1) X-rays 2) Auger electrons 3) Annihilation of positron and electron 4) Bremsstrahlung radiation eγ eγ e- e+ γ e-

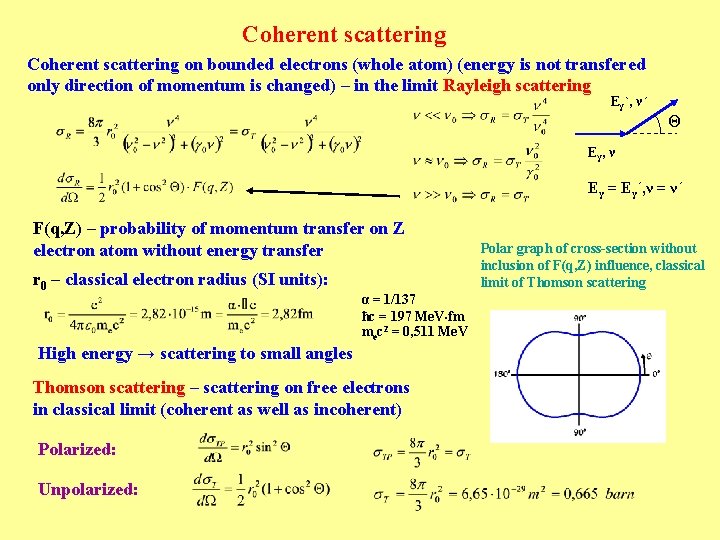
Coherent scattering on bounded electrons (whole atom) (energy is not transfered only direction of momentum is changed) – in the limit Rayleigh scattering Eγ`, ν´ Θ Eγ , ν Eγ = Eγ´, ν = ν´ F(q, Z) – probability of momentum transfer on Z electron atom without energy transfer r 0 – classical electron radius (SI units): α = 1/137 ħc = 197 Me. V fm mec 2 = 0, 511 Me. V High energy → scattering to small angles Thomson scattering – scattering on free electrons in classical limit (coherent as well as incoherent) Polarized: Unpolarized: Polar graph of cross-section without inclusion of F(q, Z) influence, classical limit of Thomson scattering

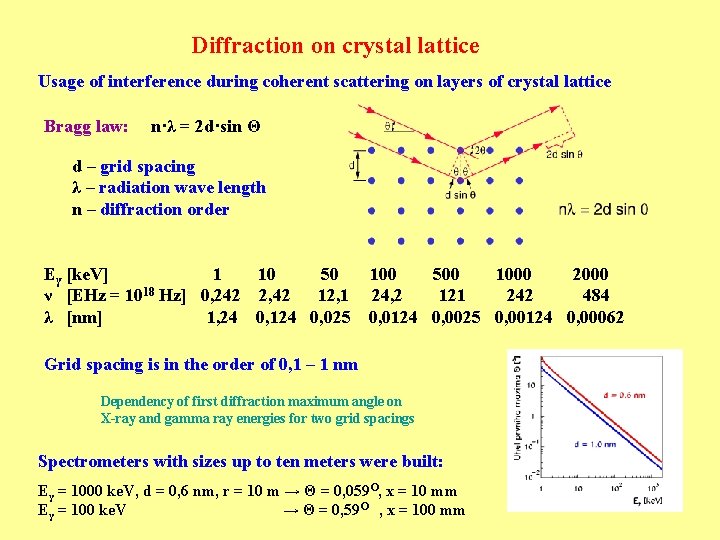
Diffraction on crystal lattice Usage of interference during coherent scattering on layers of crystal lattice Bragg law: n·λ = 2 d·sin Θ d – grid spacing λ – radiation wave length n – diffraction order Eγ [ke. V] 1 10 50 ν [EHz = 1018 Hz] 0, 242 2, 42 12, 1 λ [nm] 1, 24 0, 124 0, 025 100 500 1000 24, 2 121 242 484 0, 0124 0, 0025 0, 00124 0, 00062 Grid spacing is in the order of 0, 1 – 1 nm Dependency of first diffraction maximum angle on X-ray and gamma ray energies for two grid spacings Spectrometers with sizes up to ten meters were built: Eγ = 1000 ke. V, d = 0, 6 nm, r = 10 m → Θ = 0, 059 O, x = 10 mm Eγ = 100 ke. V → Θ = 0, 59 O , x = 100 mm

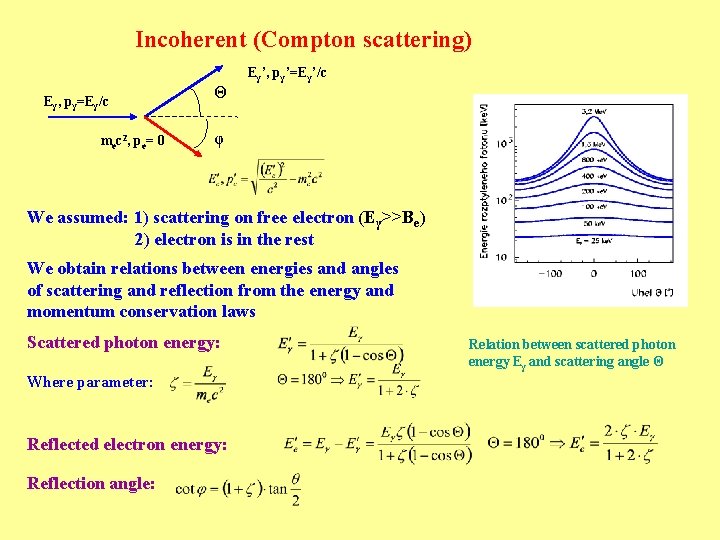
Incoherent (Compton scattering) Eγ, pγ=Eγ/c me c 2 , p e = 0 Θ Eγ’, pγ’=Eγ’/c φ We assumed: 1) scattering on free electron (Eγ>>Be) 2) electron is in the rest We obtain relations between energies and angles of scattering and reflection from the energy and momentum conservation laws Scattered photon energy: Where parameter: Reflected electron energy: Reflection angle: Relation between scattered photon energy Eγ and scattering angle Θ

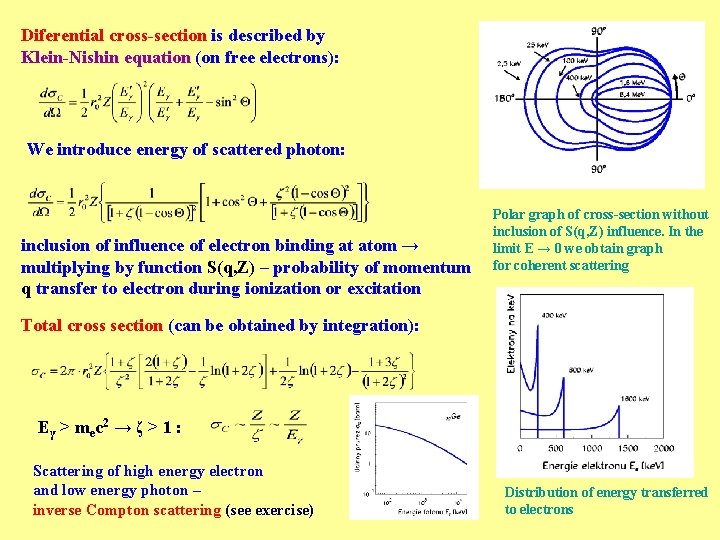
Diferential cross-section is described by Klein-Nishin equation (on free electrons): We introduce energy of scattered photon: inclusion of influence of electron binding at atom → multiplying by function S(q, Z) – probability of momentum q transfer to electron during ionization or excitation Polar graph of cross-section without inclusion of S(q, Z) influence. In the limit E → 0 we obtain graph for coherent scattering Total cross section (can be obtained by integration): Eγ > mec 2 → ζ > 1 : Scattering of high energy electron and low energy photon – inverse Compton scattering (see exercise) Distribution of energy transferred to electrons

Photoelectric effect Can pass only on bounded electron γ e- Total photon energy is transfered Electron energy: Ee = Eγ - Be Accurate calculation of photoeffect process (solution of Dirac equation) is very sophisticated: If it is enough energy (Eγ > Be. K binding energy on K-shell) the photoeffect will pass almost only on these electrons Cross-section (for Eγ << mec 2): where and so is fine structure constant σF = ~ Z 5·Eγ-3, 5 near to K-shell More accurate equation for σF near to K-shell see Leo Dependency of K-shell electron binding energy on proton number Z of atom (Si – 1, 8389 ke. V, Ge – 11. 1031 ke. V, Pb – 88. 0045 ke. V) σF = ~ Z 4, 5·Eγ-3

Production of electron and positron pairs Transformation of photon to electron and positron pair. Energy and momentum conservation laws → only γ In nucleus field (mostly) Eγ > 2 mec 2 = 1022 ke. V eventually electrons Eγ > 4 mec 2 = 2044 ke. V (je 1 -2 Z smaller) e+ e- Description is equivalent to description of bremsstrahlung radiation (necessity to include screening influence: predominance of pair production near nucleus – without screening): There is valid for cross-section in special cases: Without screening: Complete screening: where f(Z) is coulomb correction of order α 2 Production in the electron field („triplet“ production) Dependency of σP on Z and Eγ is: (for „lower energies“ range) σP ~ Z 2 ln(2 Eγ) Eγ>>mec 2 electrons and positrons are peaked forward Θ ≈ 1/ζ Cross-section dependency On photon energy

Interaction with small contribution Nuclear Rayleigh scattering Nuclear Thomson scattering – substitutions e →Ze , me → Mj and then Total cross-sections: Nuclear resonance scattering ( for example giant dipole resonance) Photonuclear reactions – resonance processes with small probability Photonuclear reactions in order of mbarn up to barn in narrow energy range interaction with electrons in order of barns up to 105 barns in broad energy range Photon interaction with coulomb field of nucleus (Delbrück scattering) – we can look on it as on virtual pair production and following annihilation

Secondary processes X-ray Fluorescent efficiency (coefficient): NX – X-ray photons NA – Auger electrons Released energy is transferred during electron transition at atomic cloud on other electron Annihilation of positron and electron Positrons are stopped by ionization losses and they annihilate in the rest → 2 quanta of 511 ke. V (they are not fully in the rest → energy smearing of annihilation quanta) Bremsstrahlung radiation during movement of electrons and positrons Passage of electrons and positrons: 1) Ionization losses 2) Bremsstrahlung radiation elektron záření gama proton Charged particle moves in nuclear field with acceleration → it emits photons

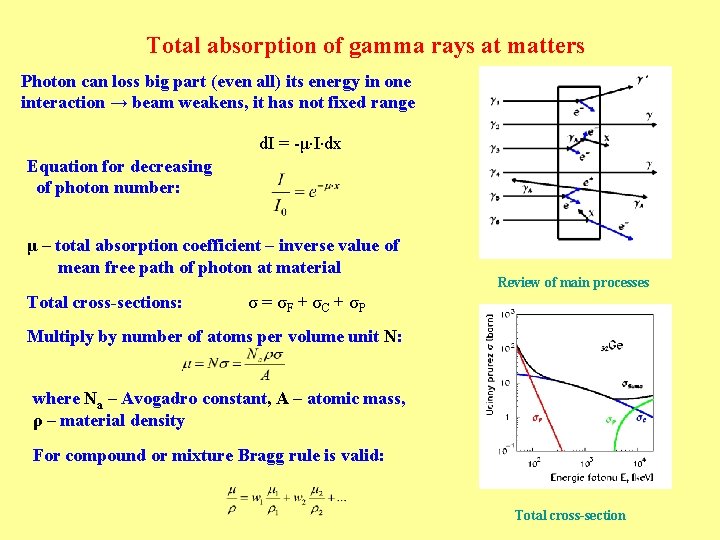
Total absorption of gamma rays at matters Photon can loss big part (even all) its energy in one interaction → beam weakens, it has not fixed range d. I = -μ I dx Equation for decreasing of photon number: μ – total absorption coefficient – inverse value of mean free path of photon at material Total cross-sections: Review of main processes σ = σF + σC + σP Multiply by number of atoms per volume unit N: where Na – Avogadro constant, A – atomic mass, ρ – material density For compound or mixture Bragg rule is valid: Total cross-section