GAMMA CAMERA traitement dimages Prsentation dimages Traitements mathmatiques

















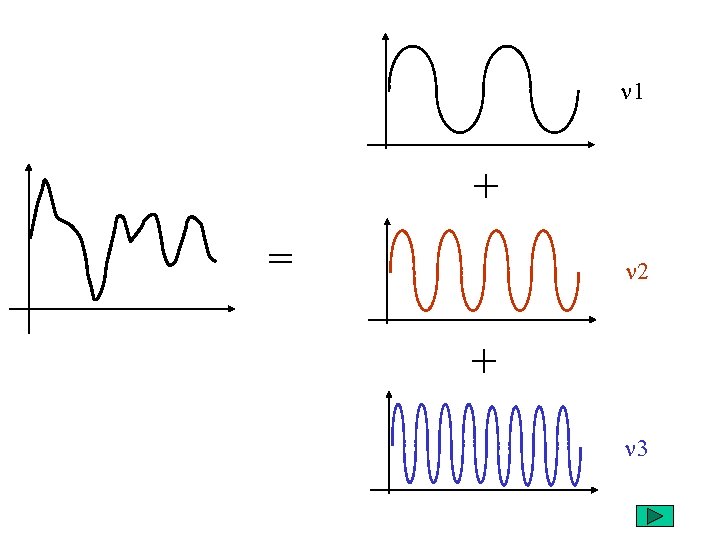















- Slides: 97

GAMMA CAMERA (traitement d’images)

Présentation d’images Traitements mathématiques Filtrage Calculs avec région d’intérêt Synchronisation Série dynamique Reconstruction tomographique

Présentation d’images

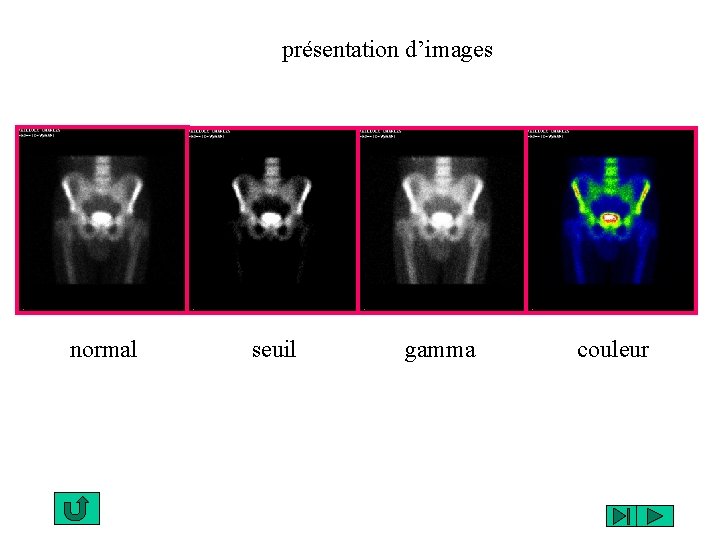
présentation d’images normal seuil gamma couleur

Traitements mathématiques

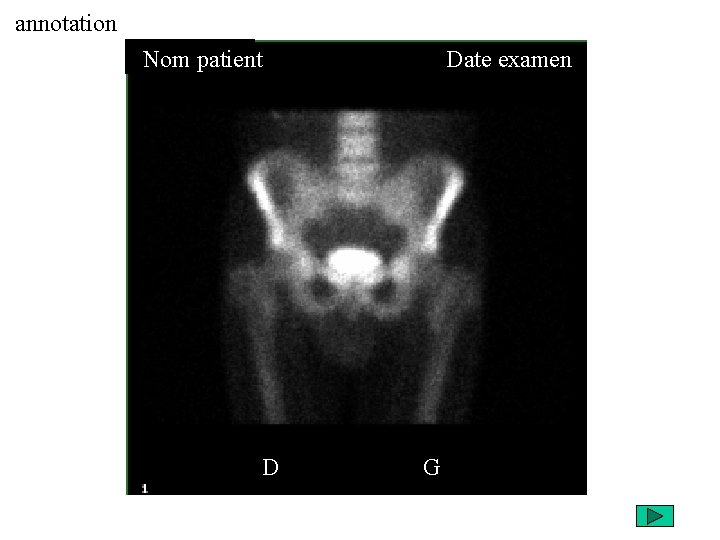
annotation Nom patient D Date examen G

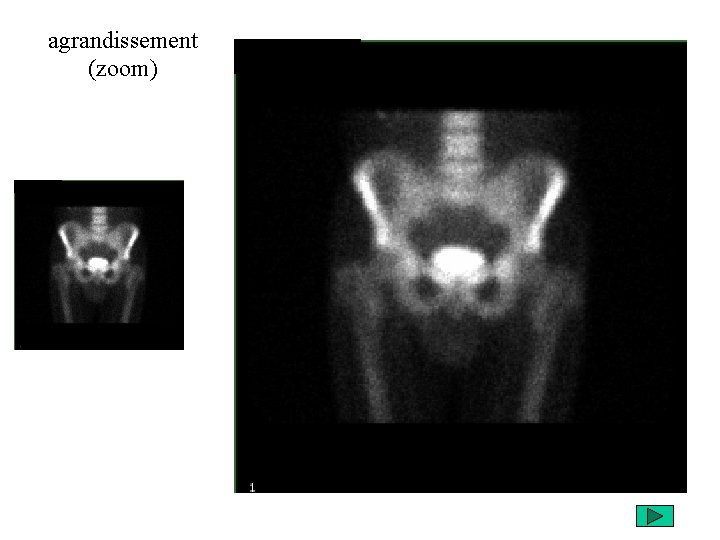
agrandissement (zoom)

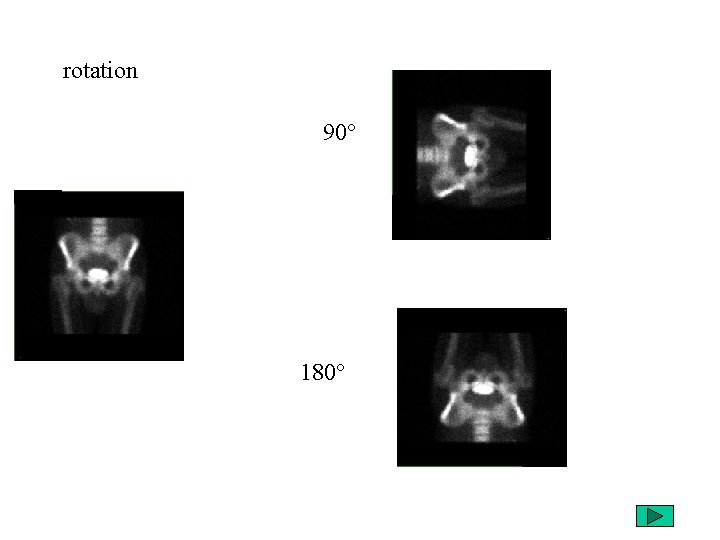
rotation 90° 180°

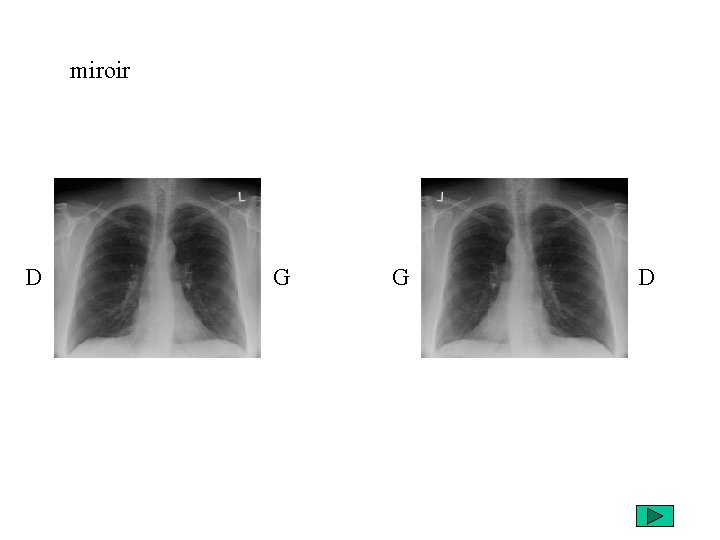
miroir D G G D

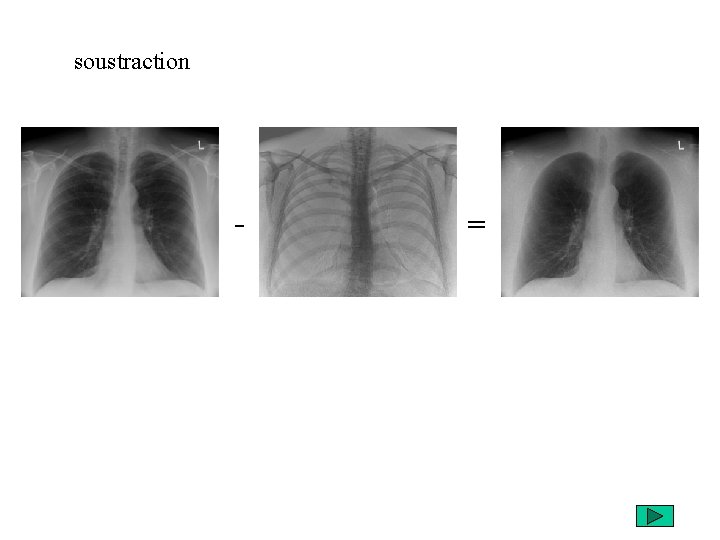
soustraction - =

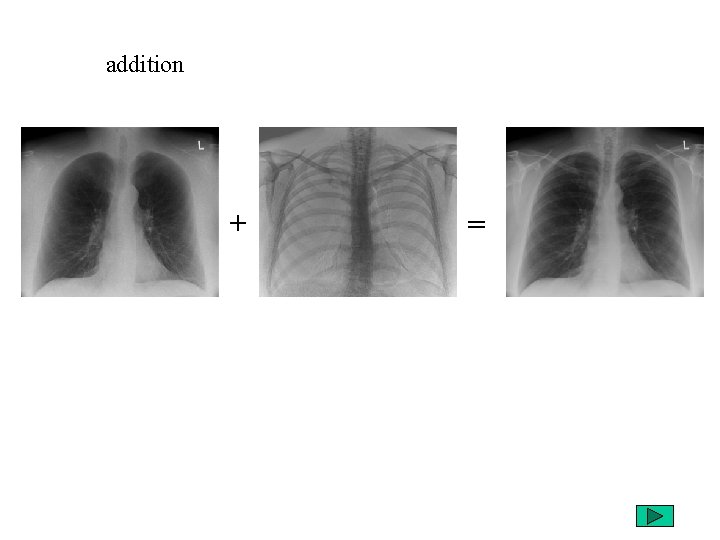
addition + =

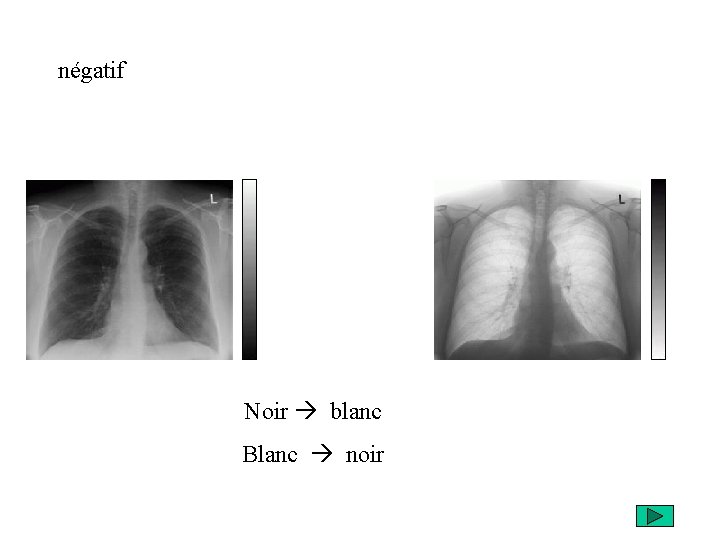
négatif Noir blanc Blanc noir

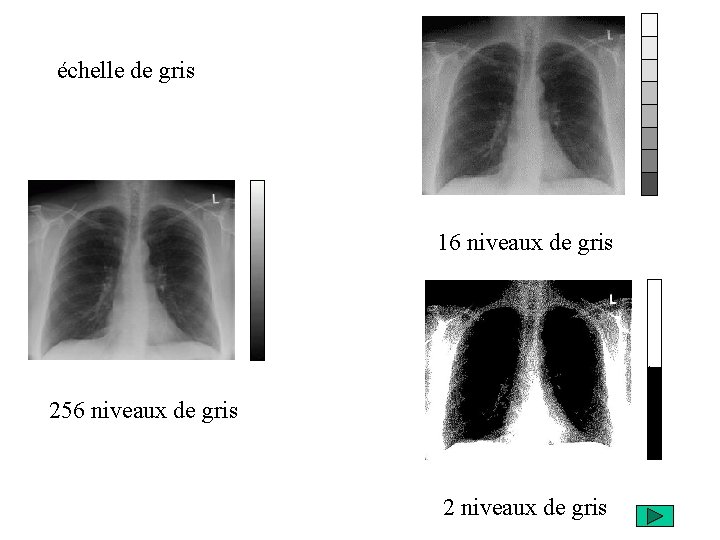
échelle de gris 16 niveaux de gris 256 niveaux de gris 2 niveaux de gris

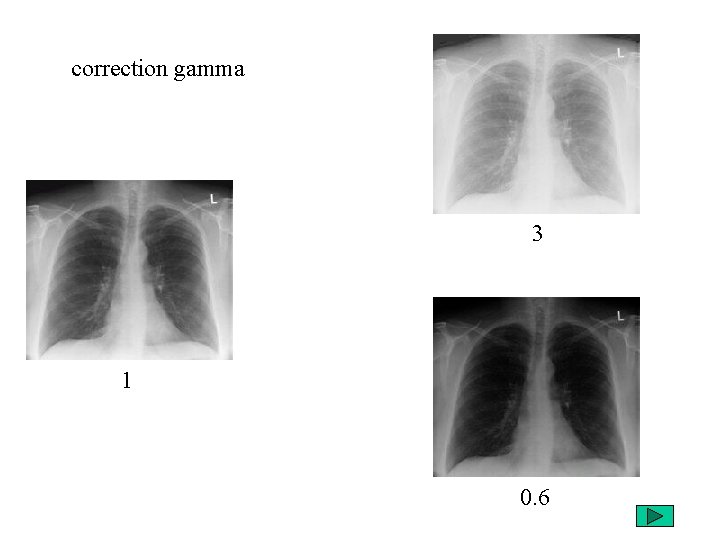
correction gamma 3 1 0. 6

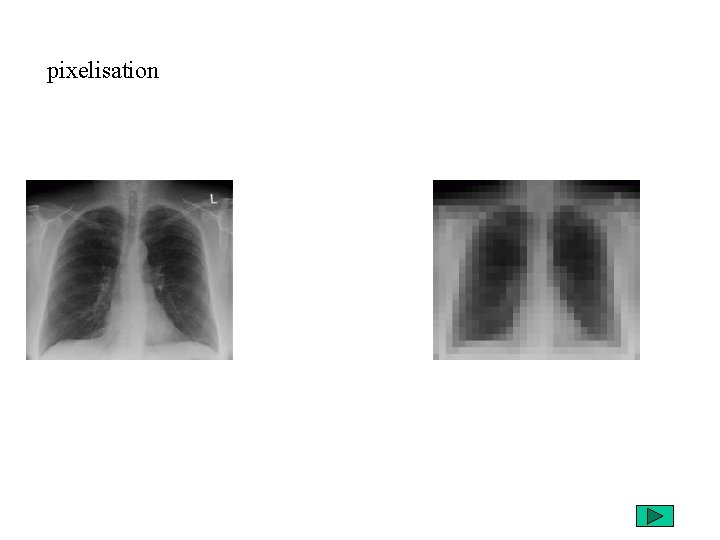
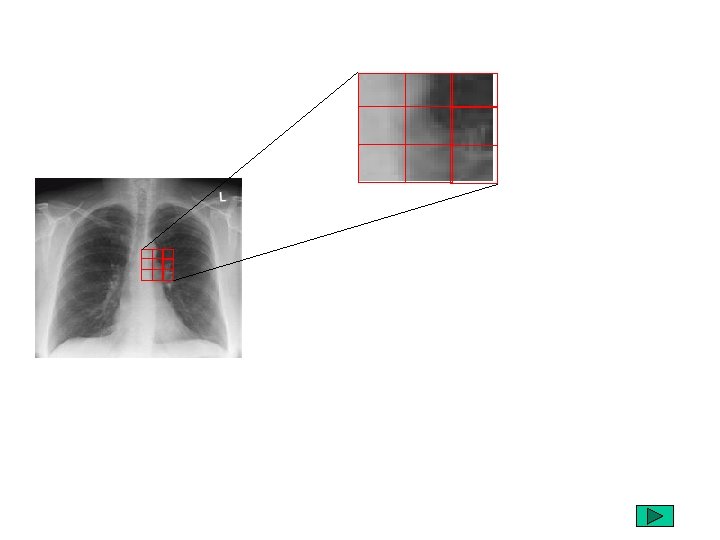
pixelisation

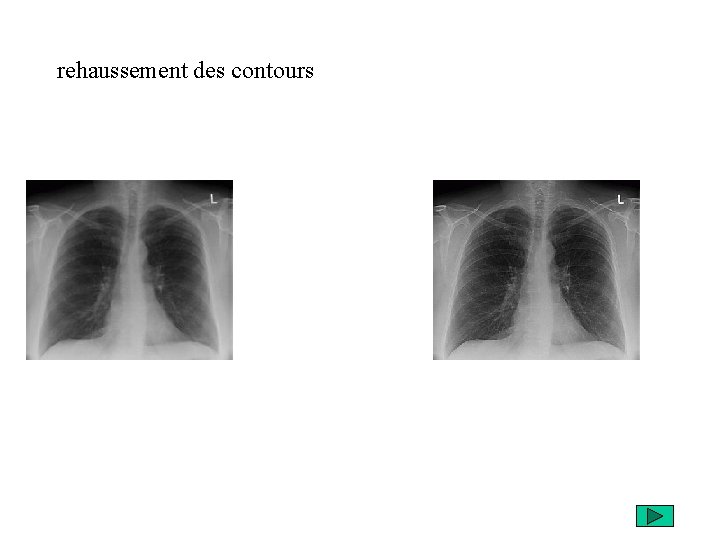
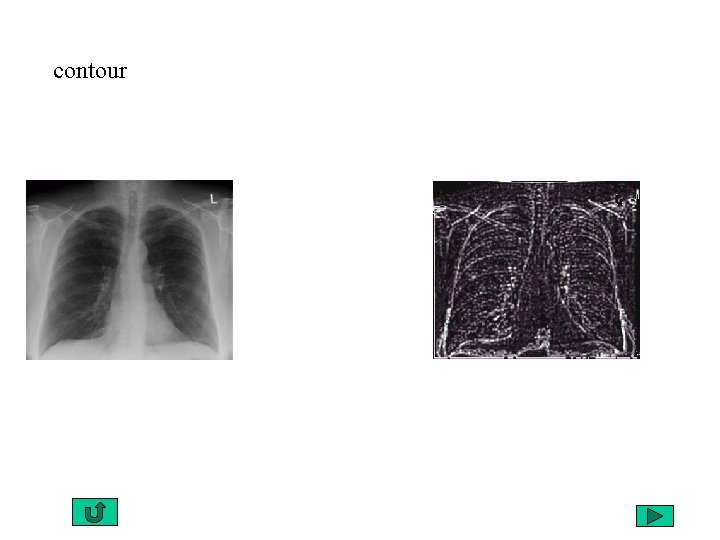
rehaussement des contours

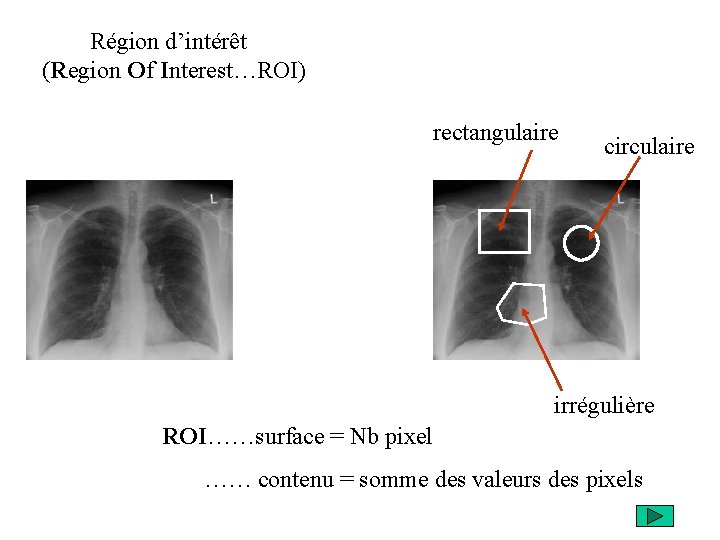
Région d’intérêt (Region Of Interest…ROI) rectangulaire circulaire irrégulière ROI……surface = Nb pixel …… contenu = somme des valeurs des pixels

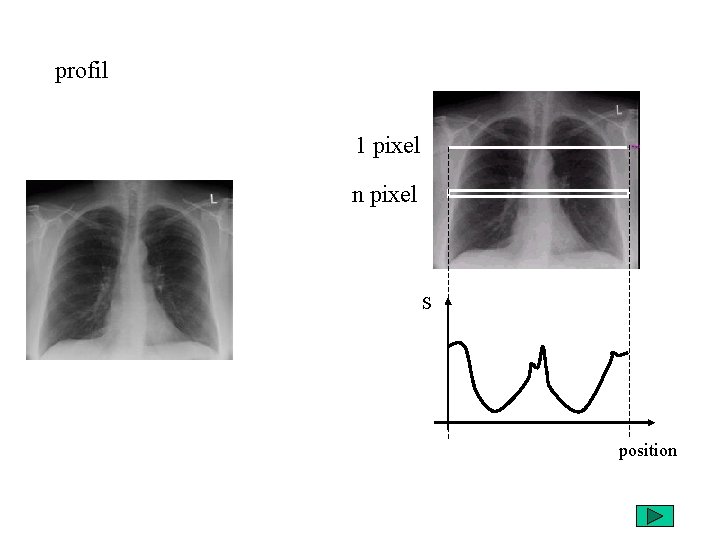
profil 1 pixel n pixel S position

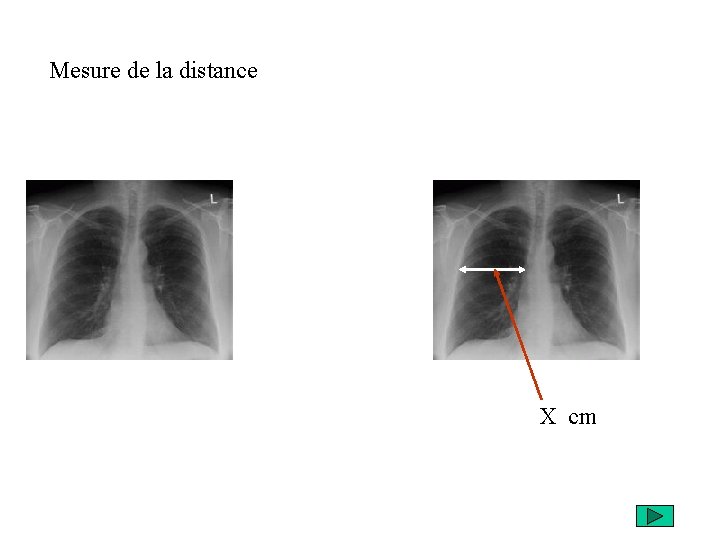
Mesure de la distance X cm

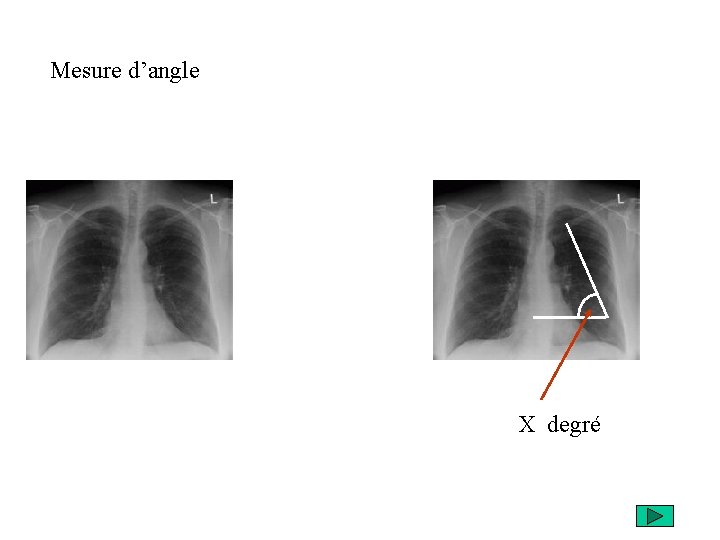
Mesure d’angle X degré

contour

Filtrage

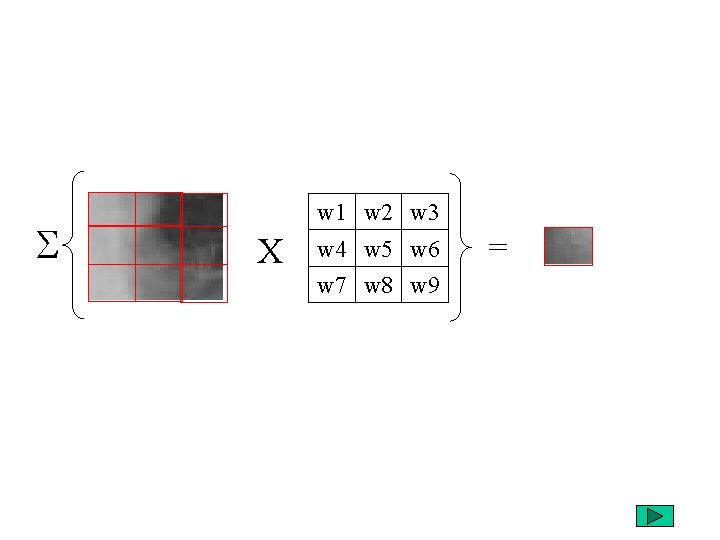
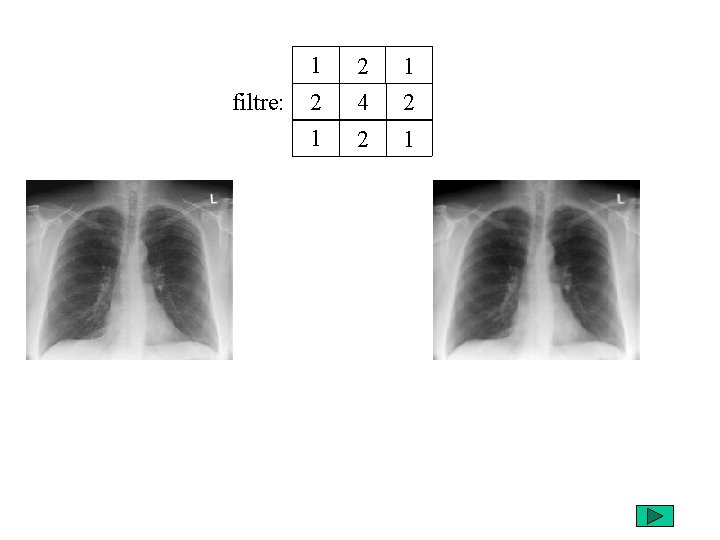
filtrage Dans le cas d’un filtrage spatiale linéaire, pour chaque pixel (i, j) de l’image F on calcule la nouvelle intensité du pixel g(i, j) par : G(i, j) = Sfiltre(m, n) * F(i-m, j-n) m = -1, 0, 1 n = -1, 0, 1

filtre: w 1 w 2 w 3 w 4 w 5 w 6 w 7 w 8 w 9

On peut écrire: G(i, j)= w 1*F(i-1, j-1) + w 2* F(i, j-1) + w 3* F(i+1, j-1) + w 4* F(i-1, j) + w 5* F(i, j) + w 6* F(i+1, j) + w 7* F(i-1, j+1) + w 8* F(i, j+1) + w 9* F(i+1, j+1)


S w 1 w 2 w 3 X w 4 w 5 w 6 w 7 w 8 w 9 =

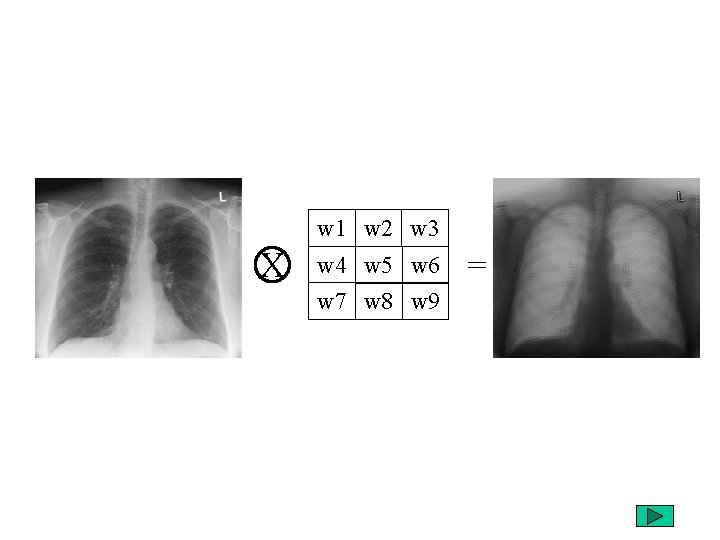
w 1 w 2 w 3 X w 4 w 5 w 6 w 7 w 8 w 9 =

filtre: 1 2 4 2 1

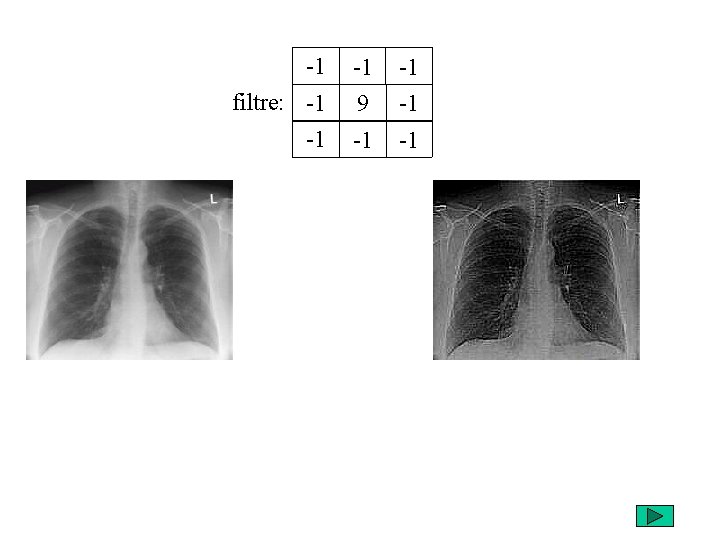
-1 -1 -1 filtre: -1 9 -1 -1

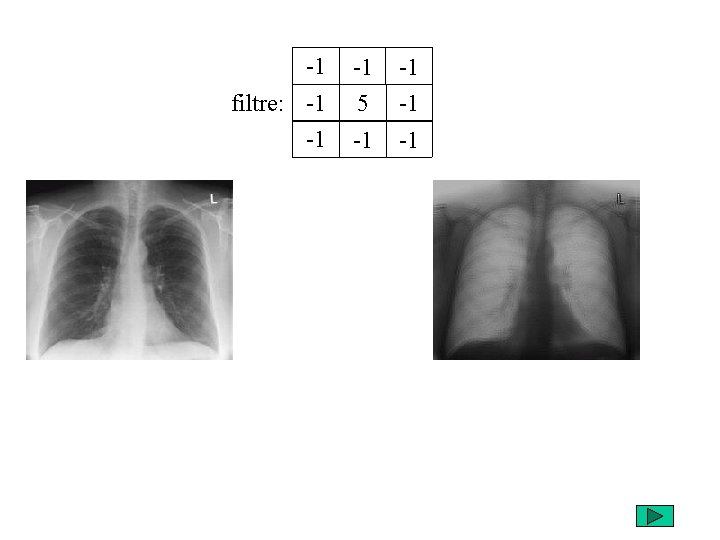
-1 -1 -1 filtre: -1 5 -1 -1

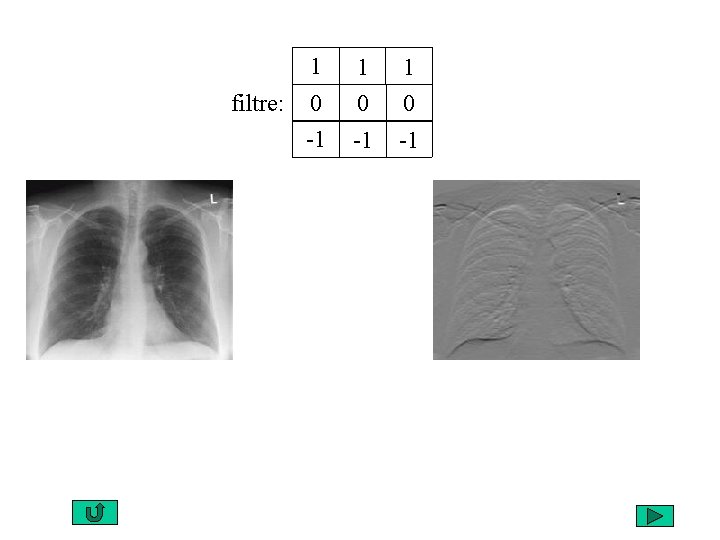
filtre: 1 1 1 0 0 0 -1 -1 -1

Calculs avec région d’intérêt (Region Of Interest)

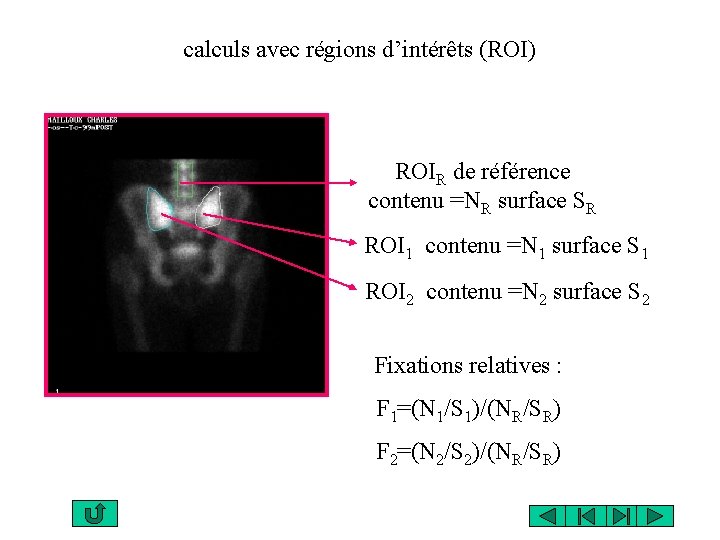
calculs avec régions d’intérêts (ROI) ROIR de référence contenu =NR surface SR ROI 1 contenu =N 1 surface S 1 ROI 2 contenu =N 2 surface S 2 Fixations relatives : F 1=(N 1/S 1)/(NR/SR) F 2=(N 2/S 2)/(NR/SR)

Synchronisation

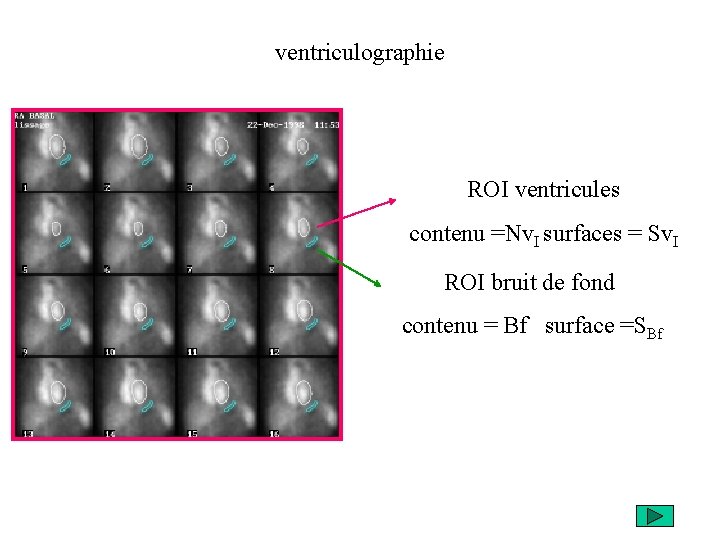
ventriculographie ROI ventricules contenu =Nv. I surfaces = Sv. I ROI bruit de fond contenu = Bf surface =SBf

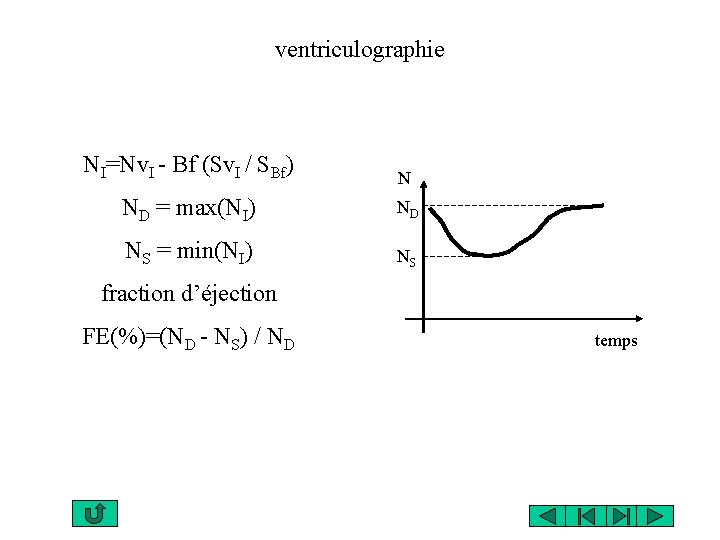
ventriculographie NI=Nv. I - Bf (Sv. I / SBf) N ND = max(NI) ND NS = min(NI) NS fraction d’éjection FE(%)=(ND - NS) / ND temps

Série dynamique

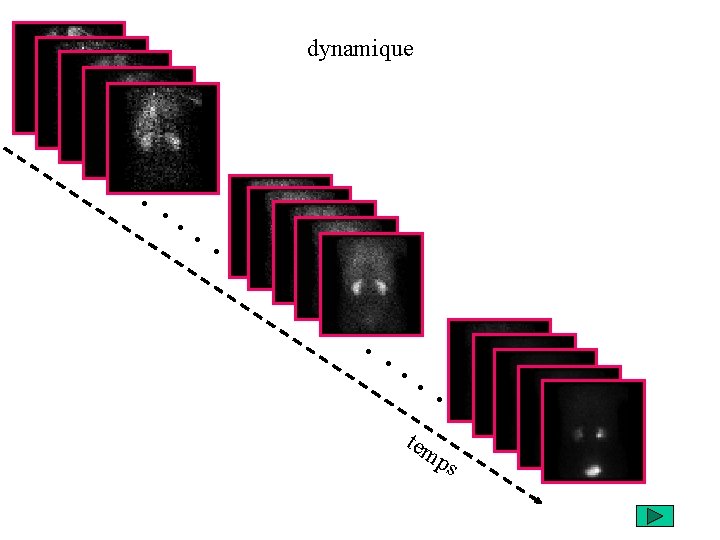
dynamique . . tem ps

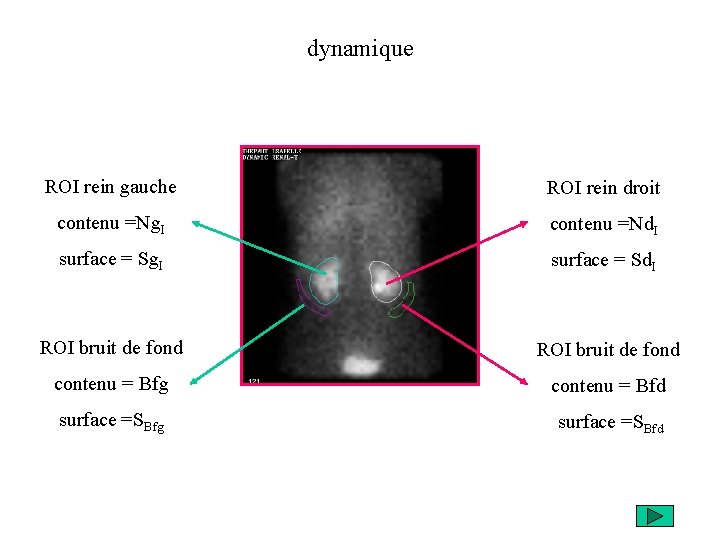
dynamique ROI rein gauche ROI rein droit contenu =Ng. I contenu =Nd. I surface = Sg. I surface = Sd. I ROI bruit de fond contenu = Bfg contenu = Bfd surface =SBfg surface =SBfd

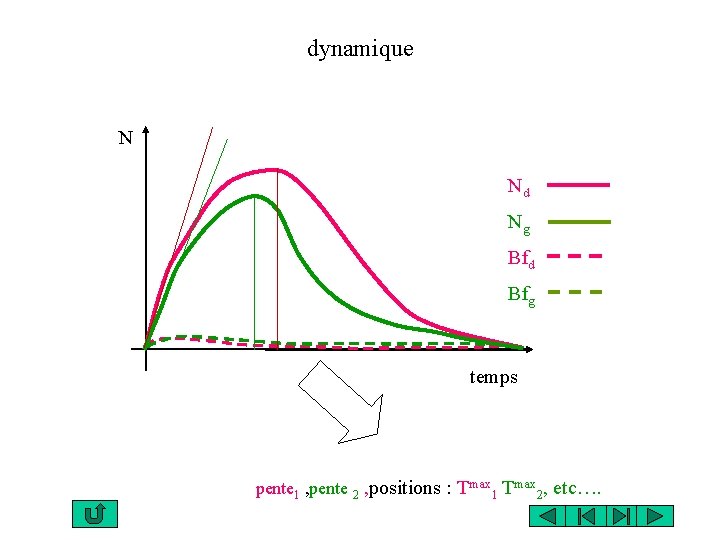
dynamique N Nd Ng Bfd Bfg temps pente 1 , pente 2 , positions : Tmax 1 Tmax 2, etc….

Reconstruction tomographique

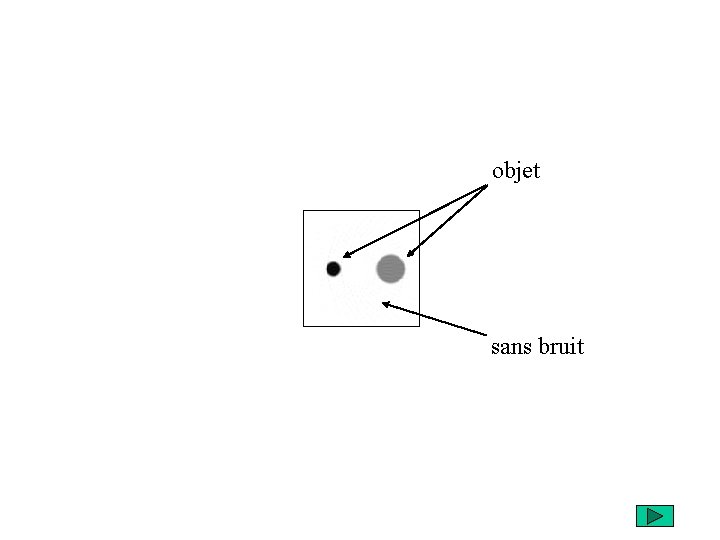
objet sans bruit

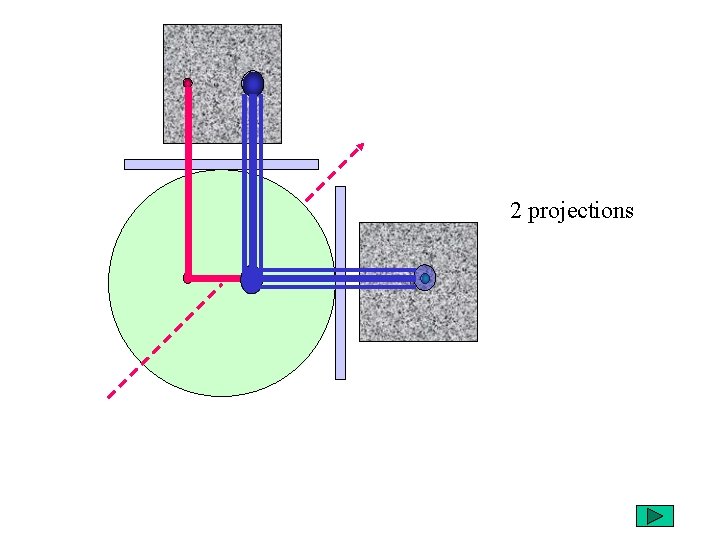
2 projections


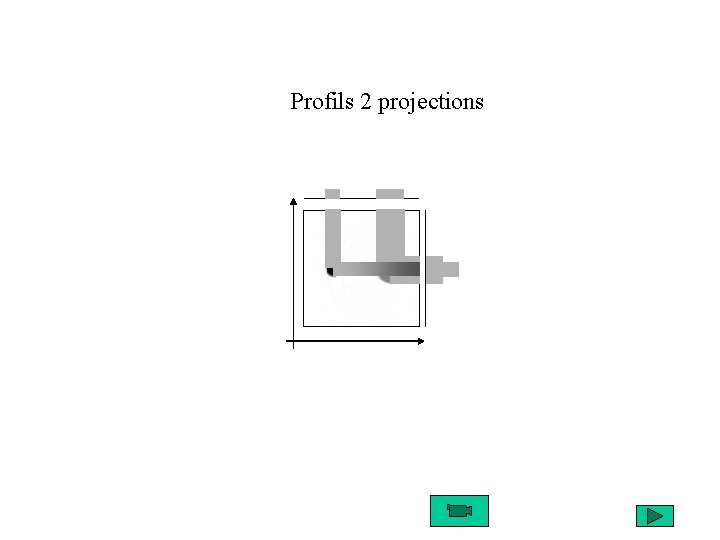
Profils 2 projections

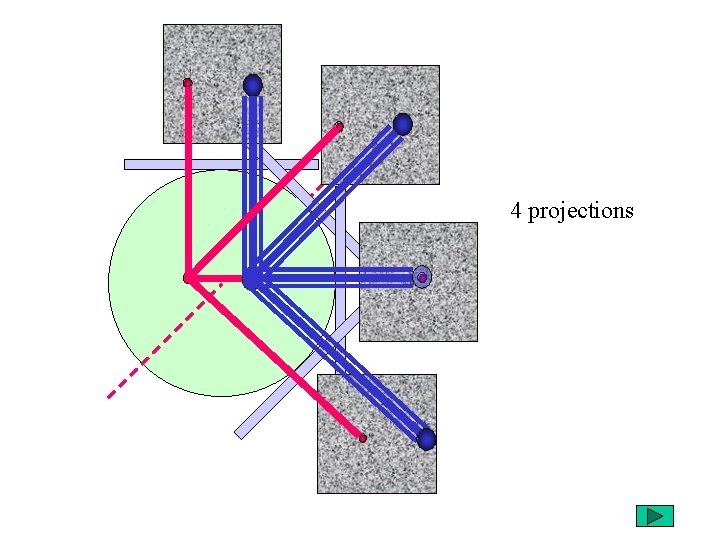
4 projections


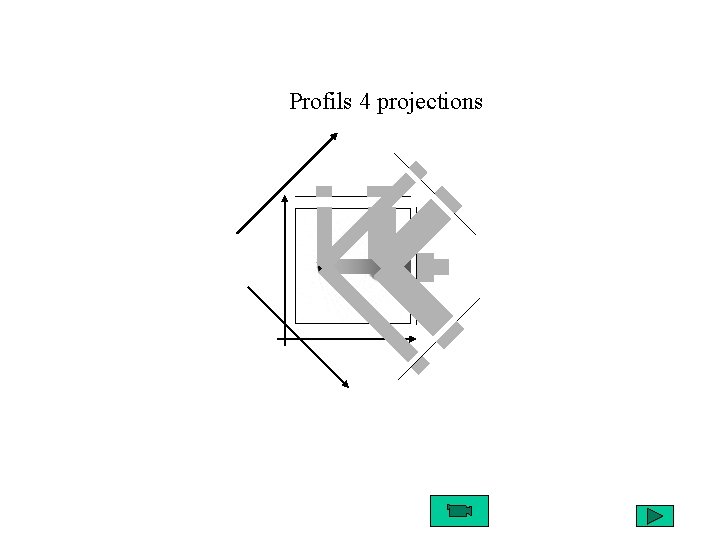
Profils 4 projections

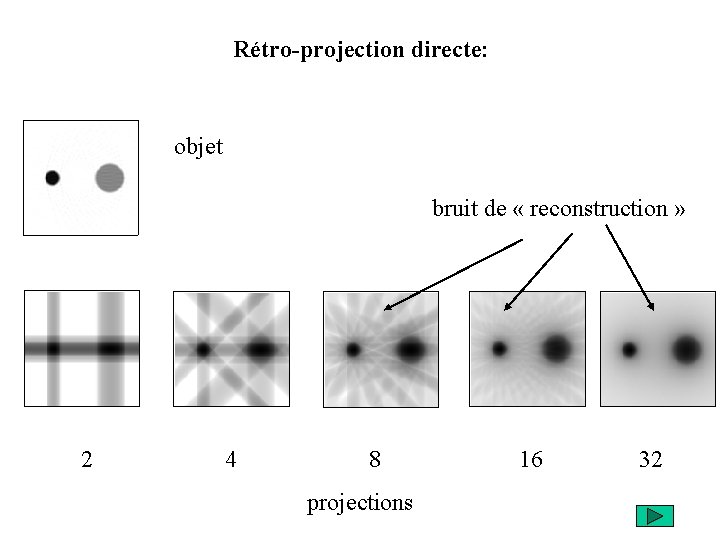
Rétro-projection directe


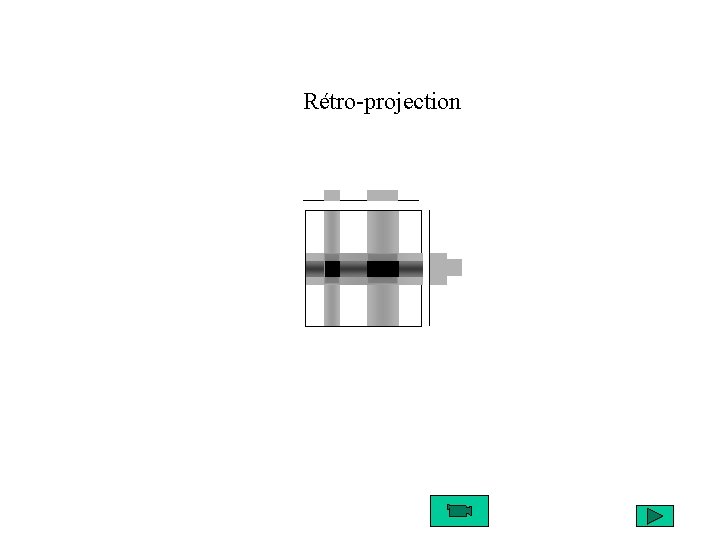
Rétro-projection

Rétro-projection directe: objet bruit de « reconstruction » 2 4 8 16 32 projections

Transformation de Fourier (FT)

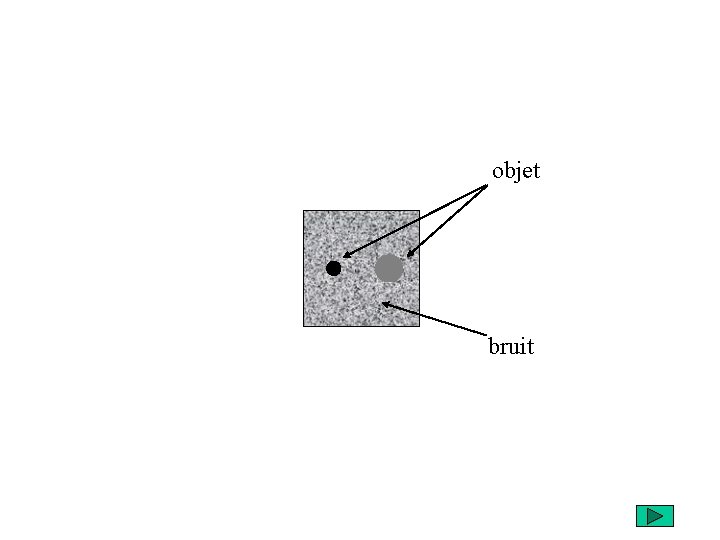
objet bruit

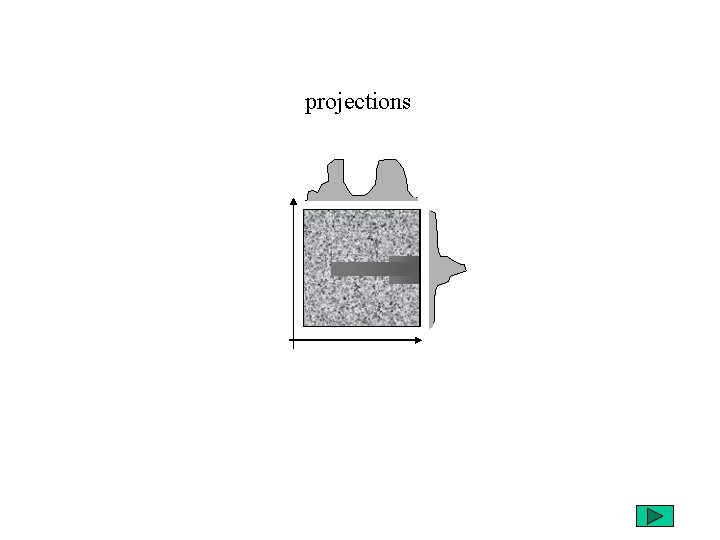
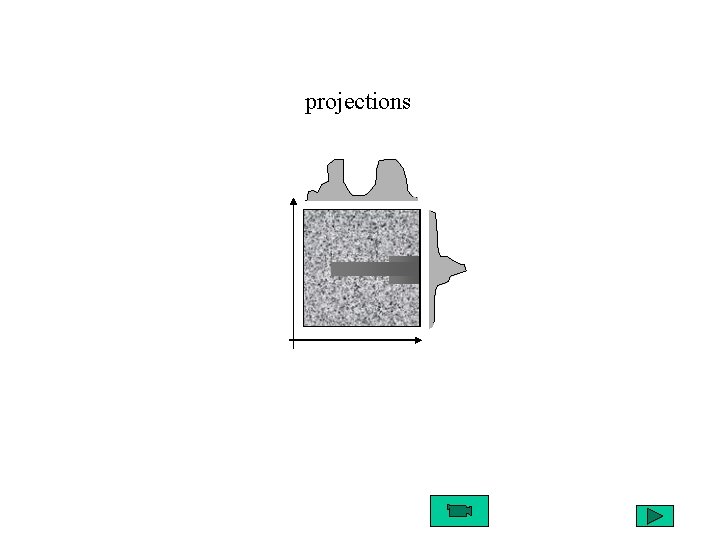
projections

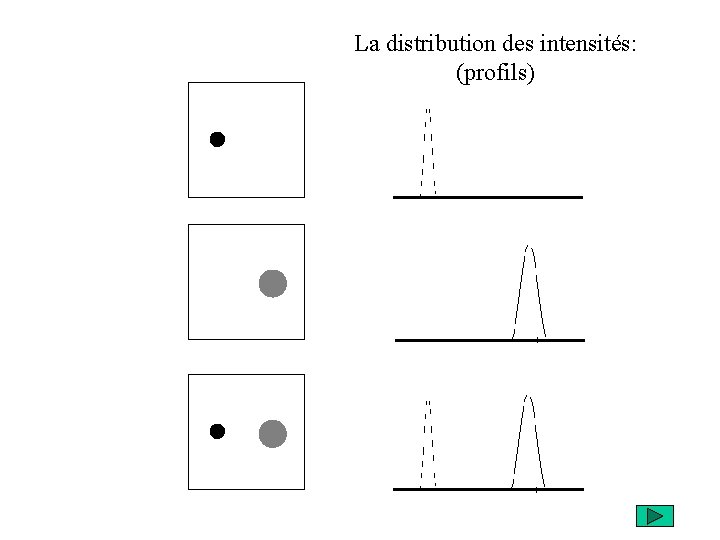
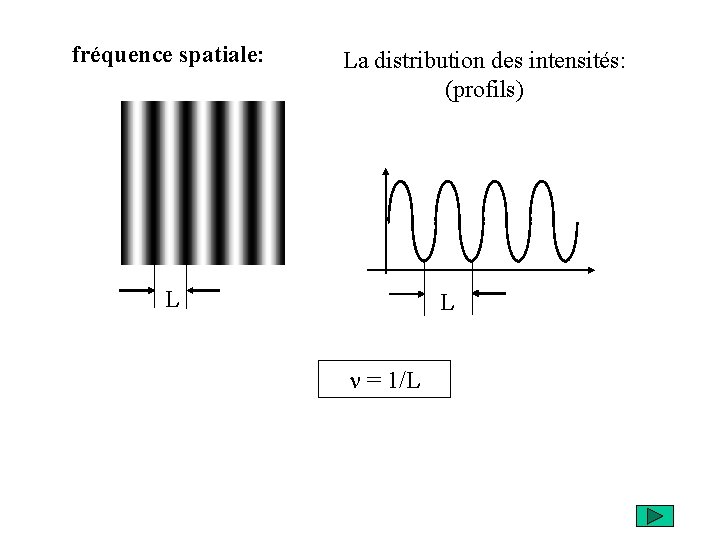
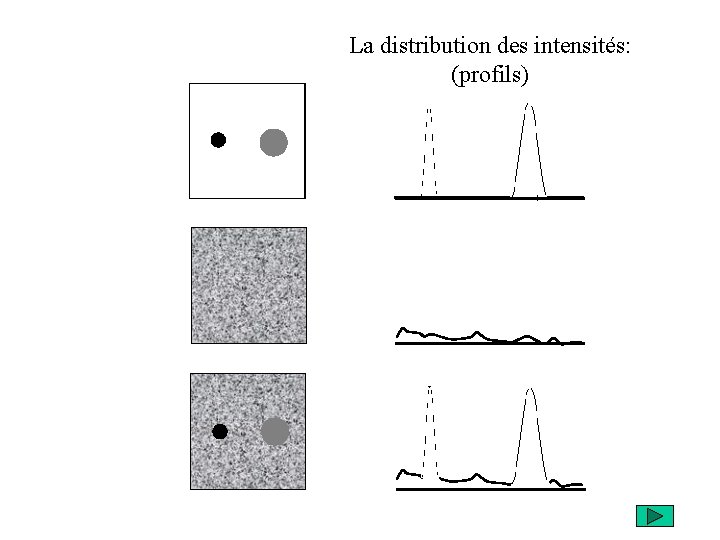
La distribution des intensités: (profils)

fréquence spatiale: La distribution des intensités: (profils) L L n = 1/L

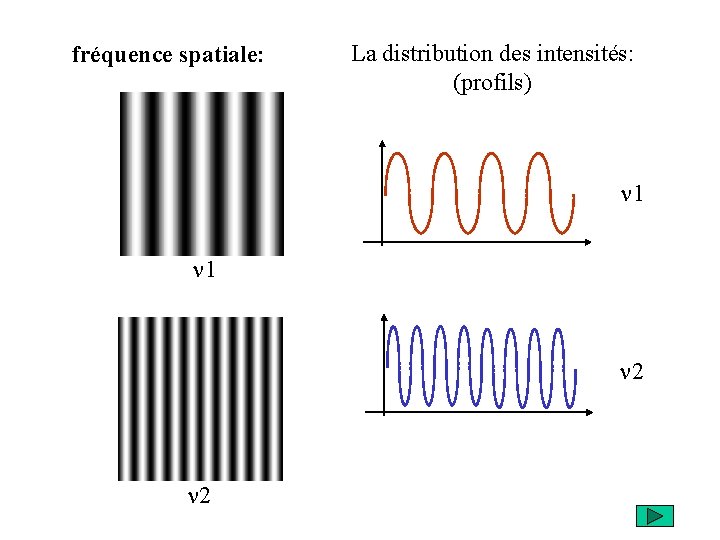
fréquence spatiale: La distribution des intensités: (profils) n 1 n 2

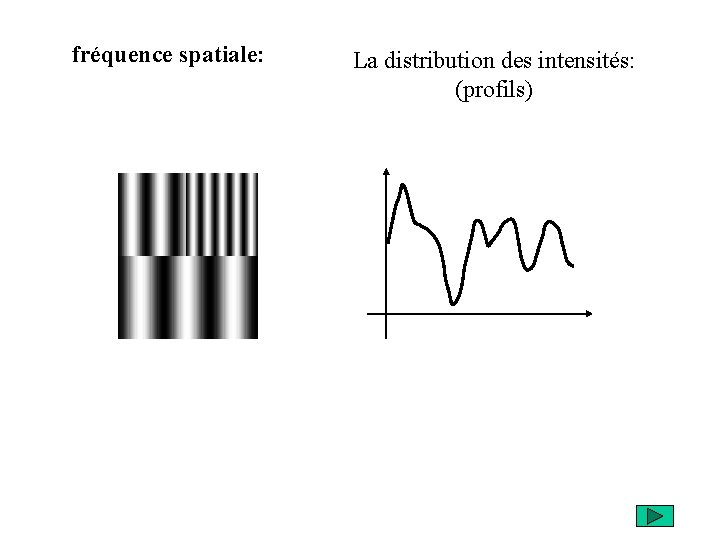
fréquence spatiale: La distribution des intensités: (profils)
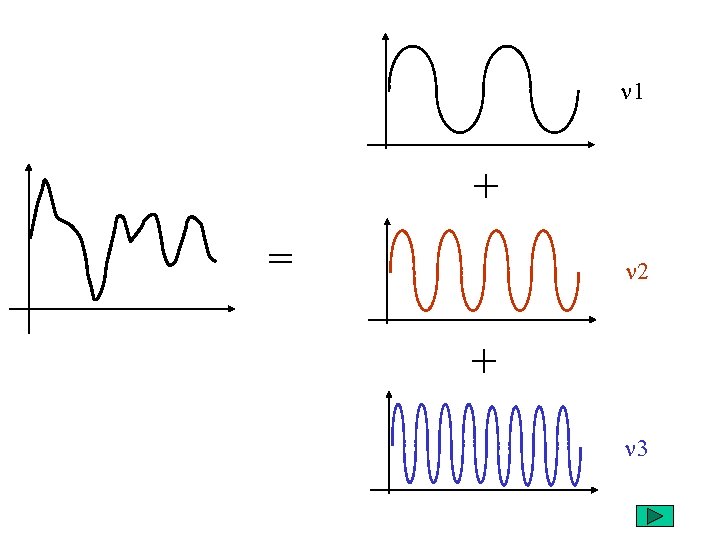
n 1 + = n 2 + n 3

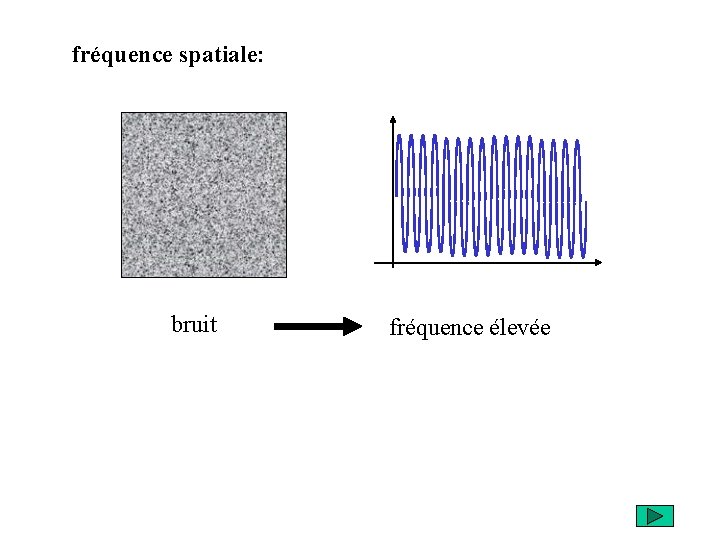
fréquence spatiale: bruit fréquence élevée

La distribution des intensités: (profils)

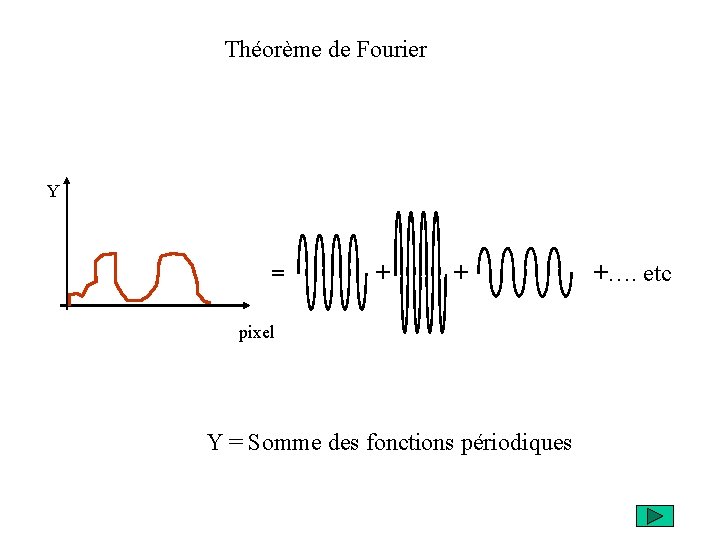
Théorème de Fourier Un signal périodique g(t), de fréquence n, peut s'écrire sous la forme d'une somme infinie de signaux périodiques (les harmoniques) sinusoïdaux et cosinusoïdaux dont la fréquence de chaque signal périodique est un multiple entier de la fréquence n du signal g(t). Si le signal n'est pas périodique, il est possible d'appliquer Fourier sur des portions du signal.

Théorème de Fourier Y = + + pixel Y = Somme des fonctions périodiques +…. etc

transformation de Fourier transformation directe transformation inverse

transformation de Fourier discrète

transformation de Fourier discrète

transformation de Fourier bidimensionnelle

transformation de Fourier bidimensionnelle discrète

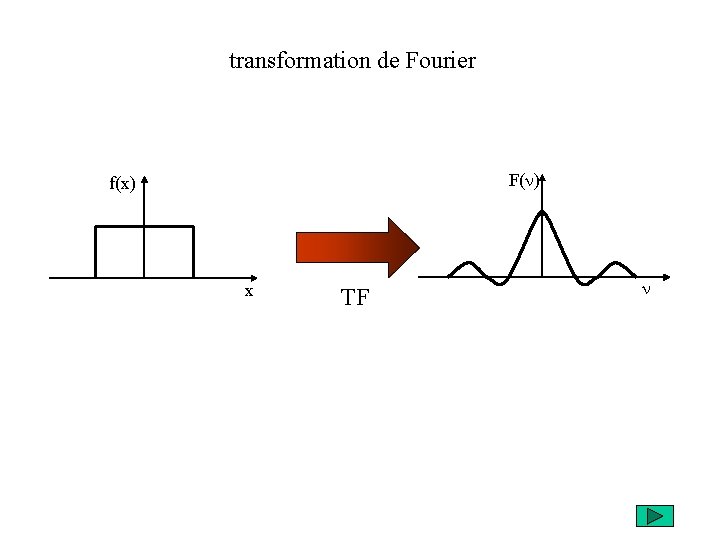
transformation de Fourier F(n) f(x) x TF n

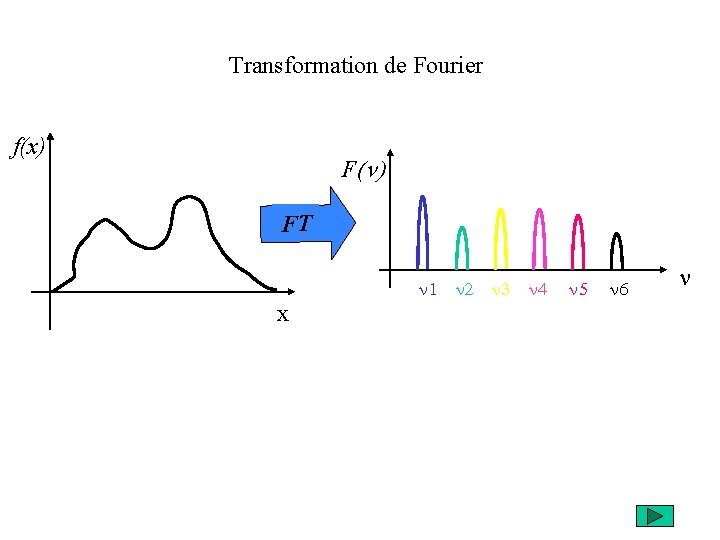
Transformation de Fourier f(x) F(n) FT n 1 x n 2 n 3 n 4 n 5 n 6 n

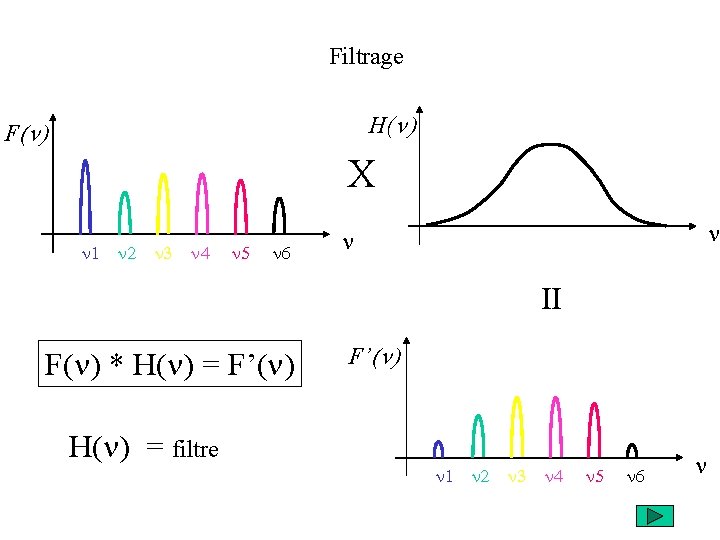
Filtrage H(n) F(n) X n 1 n 2 n 3 n 4 n 5 n 6 n n II F(n) * H(n) = F’(n) H(n) = filtre n 1 n 2 n 3 n 4 n 5 n 6 n

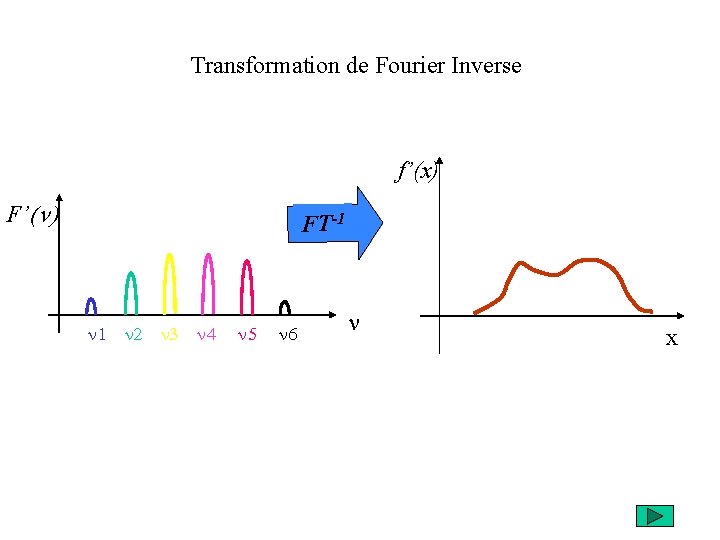
Transformation de Fourier Inverse f’(x) F’(n) FT-1 n 2 n 3 n 4 n 5 n 6 n x

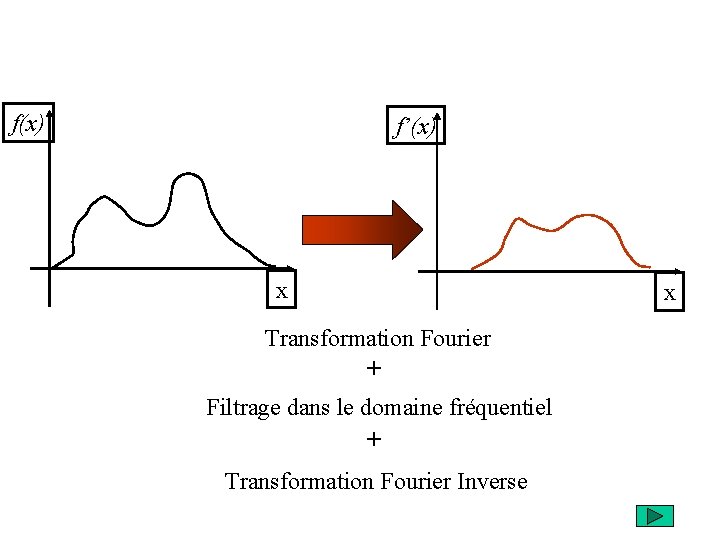
f(x) f’(x) x Transformation Fourier + Filtrage dans le domaine fréquentiel + Transformation Fourier Inverse x


projections

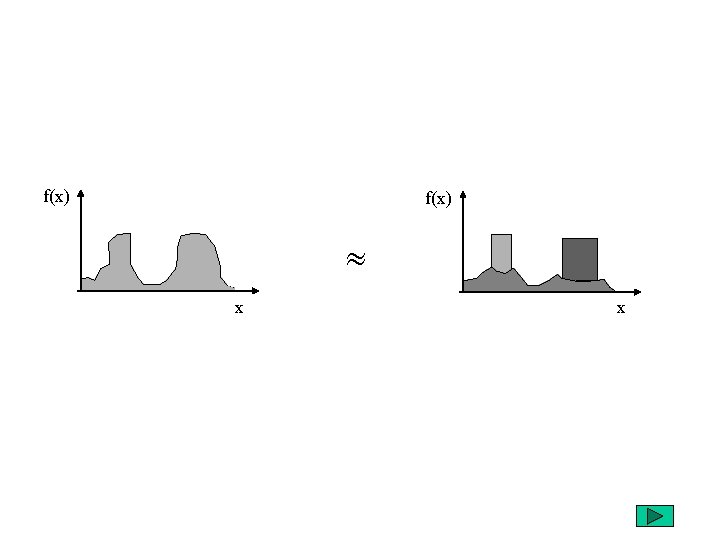
f(x) x x

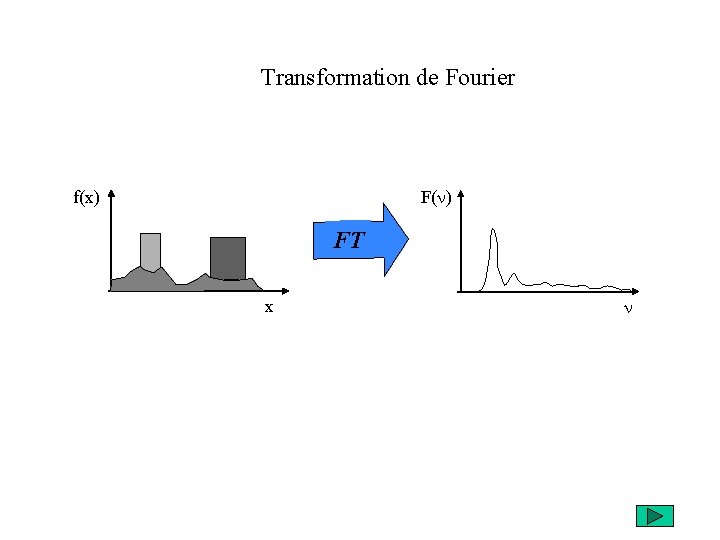
Transformation de Fourier f(x) F(n) FT x n

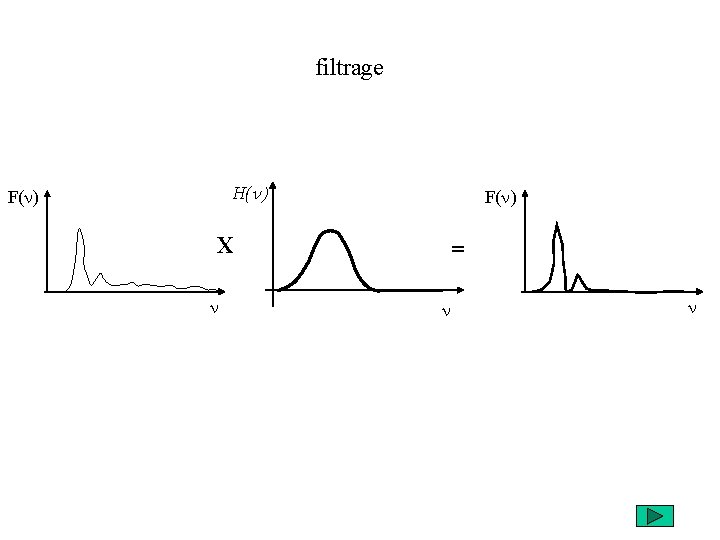
filtrage H(n) F(n) X n = n n

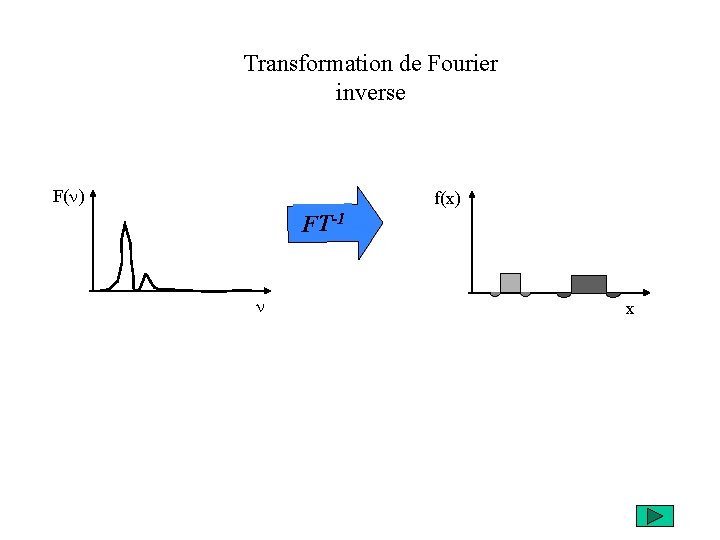
Transformation de Fourier inverse F(n) f(x) FT-1 n x


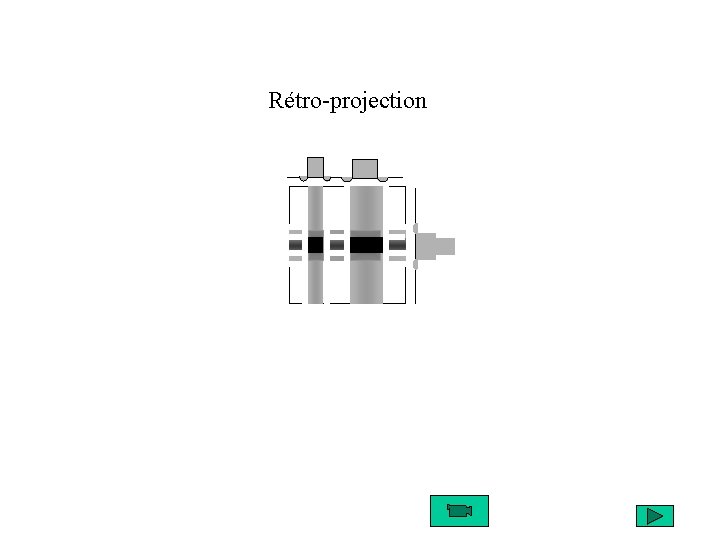
Rétro-projection

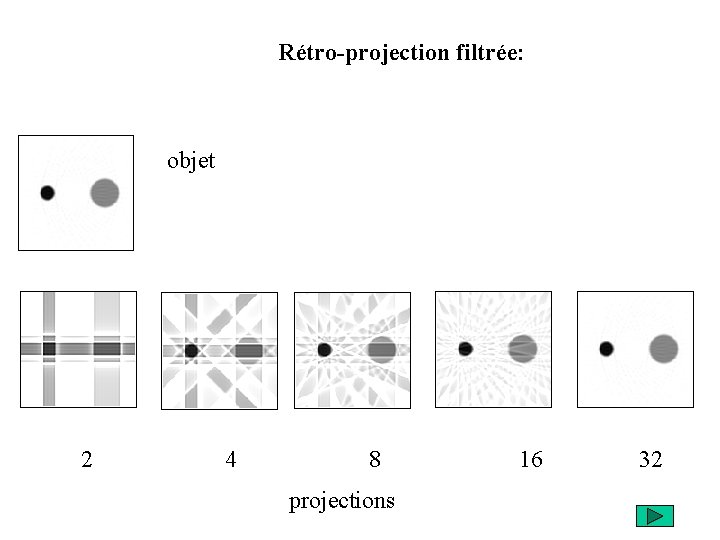
Rétro-projection filtrée: objet 2 4 8 16 32 projections

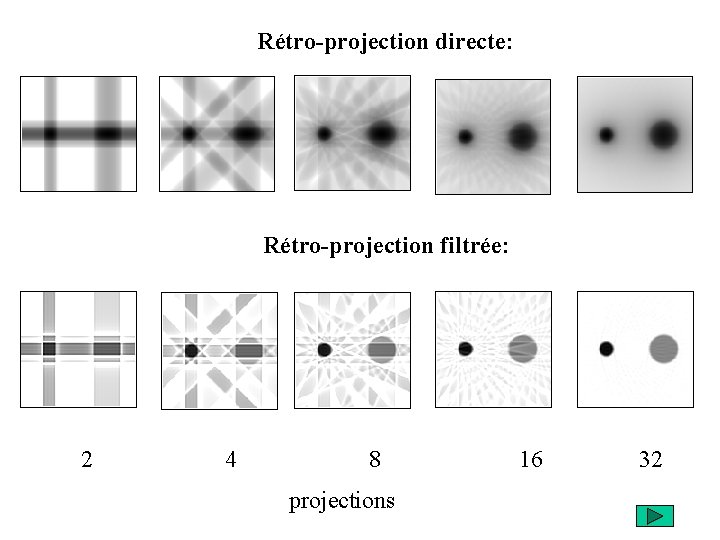
Rétro-projection directe: Rétro-projection filtrée: 2 4 8 16 32 projections

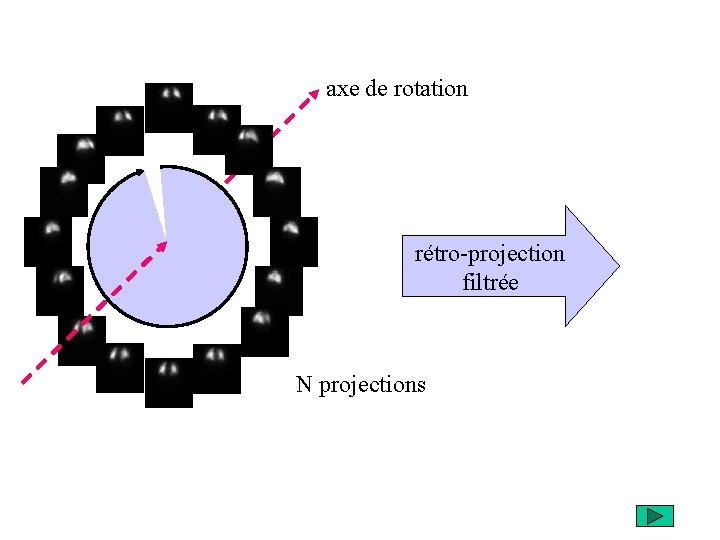
axe de rotation rétro-projection filtrée N projections


Nz coupes transversales de Nx*Ny pixels

Matrice 3 D (Nx*Ny*Nz)

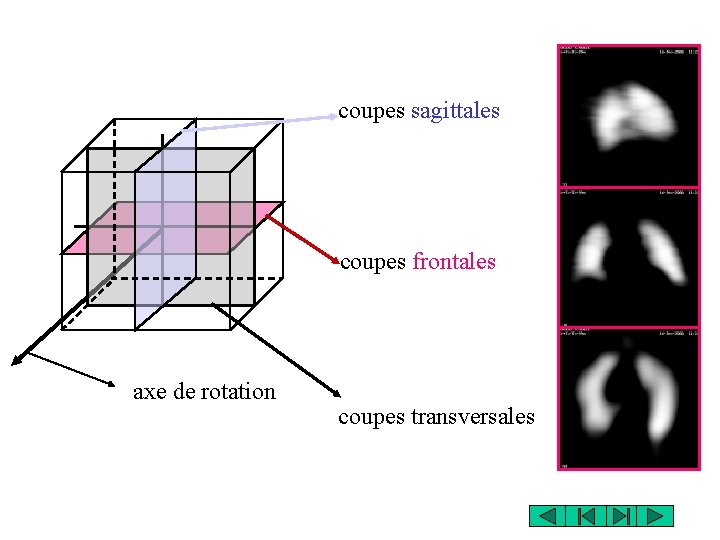
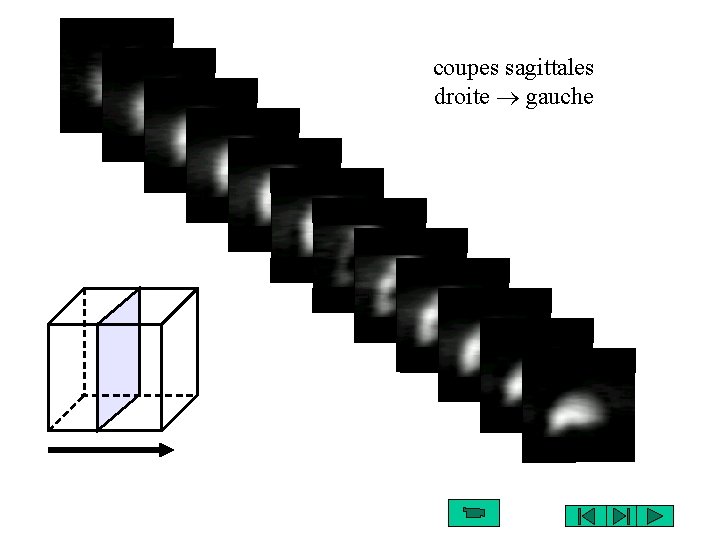
coupes sagittales coupes frontales axe de rotation coupes transversales


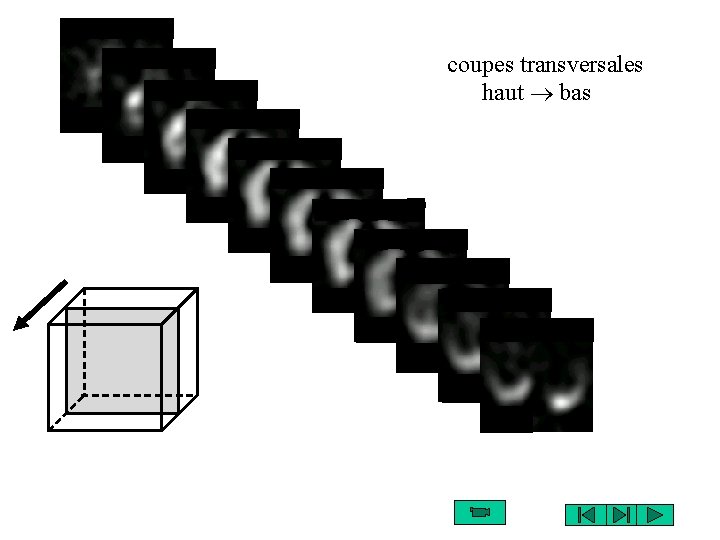
coupes transversales haut bas


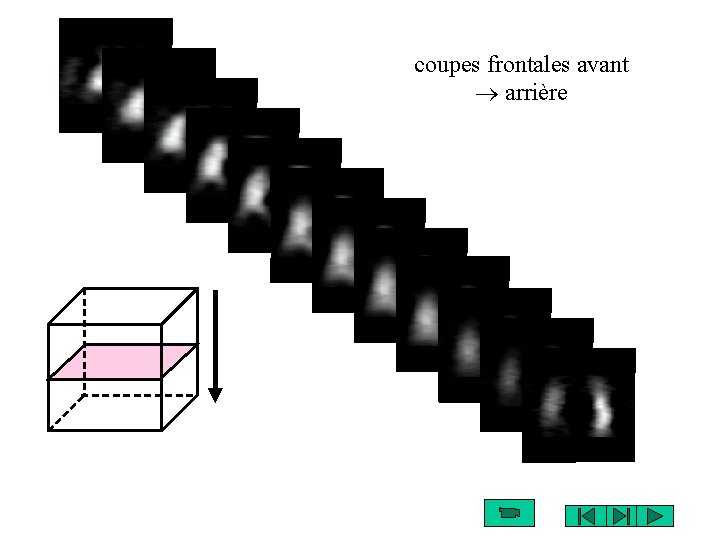
coupes frontales avant arrière c


coupes sagittales droite gauche

FIN