Games with Simultaneous Moves I Discrete Strategies Outline

Games with Simultaneous Moves I : Discrete Strategies

Outline n n n n Games with simultaneous moves Nash Equilibrium Dominance Minimax in Zero-sum Game Three Players Multiple/Zero Equilibria in pure strategies Tree Forms into Strategic Forms

Games with Simultaneous Moves n Simultaneous moves? Strategy vs. action n Discrete/Continuous strategy

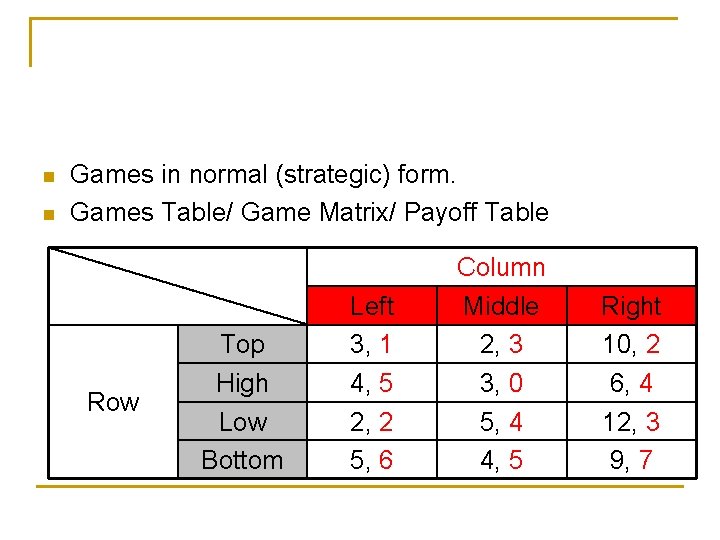
n n Games in normal (strategic) form. Games Table/ Game Matrix/ Payoff Table Row Top High Low Bottom Left 3, 1 4, 5 2, 2 5, 6 Column Middle 2, 3 3, 0 5, 4 4, 5 Right 10, 2 6, 4 12, 3 9, 7

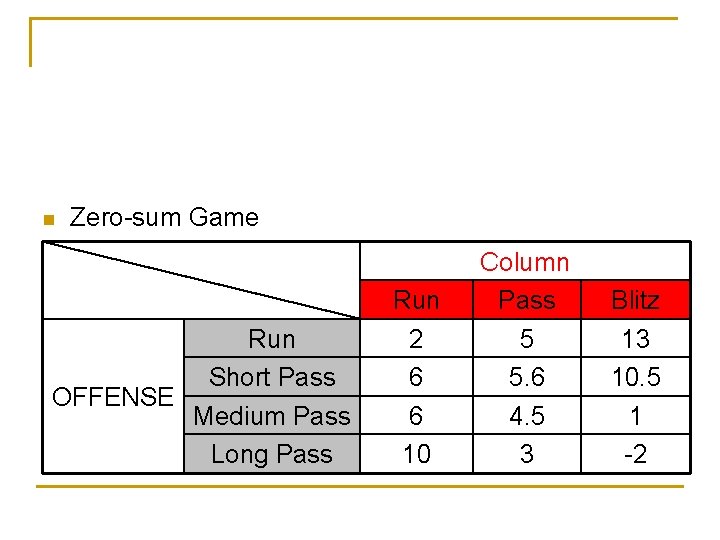
n Zero-sum Game Run Short Pass OFFENSE Medium Pass Long Pass Run 2 6 6 10 Column Pass 5 5. 6 4. 5 3 Blitz 13 10. 5 1 -2

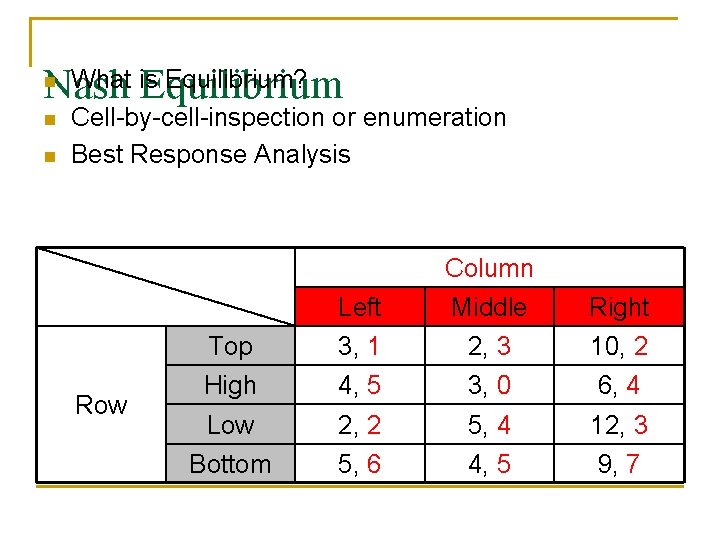
n What is Equilibrium? Nash Equilibrium n n Cell-by-cell-inspection or enumeration Best Response Analysis Column Row Left Middle Right Top 3, 1 2, 3 10, 2 High 4, 5 3, 0 6, 4 Low 2, 2 5, 4 12, 3 Bottom 5, 6 4, 5 9, 7

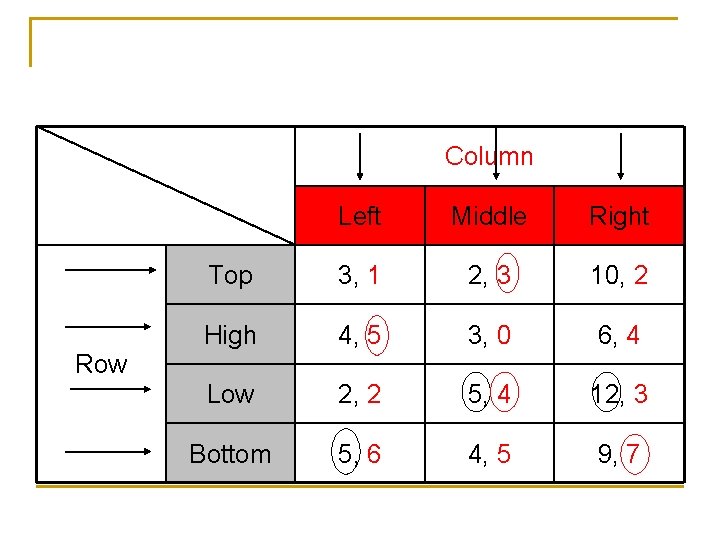
Column Left Middle Right Top 3, 1 2, 3 10, 2 High 4, 5 3, 0 6, 4 Low 2, 2 5, 4 12, 3 Bottom 5, 6 4, 5 9, 7 Row

n The N. E is (Low, Middle) →(5, 4) n A Nash Equilibrium in a game is a list of strategies, one for each player, such that no player can get a better payoff by switching to some other strategy that is available to her while all the other players adhere to the strategies specified for them in the list.

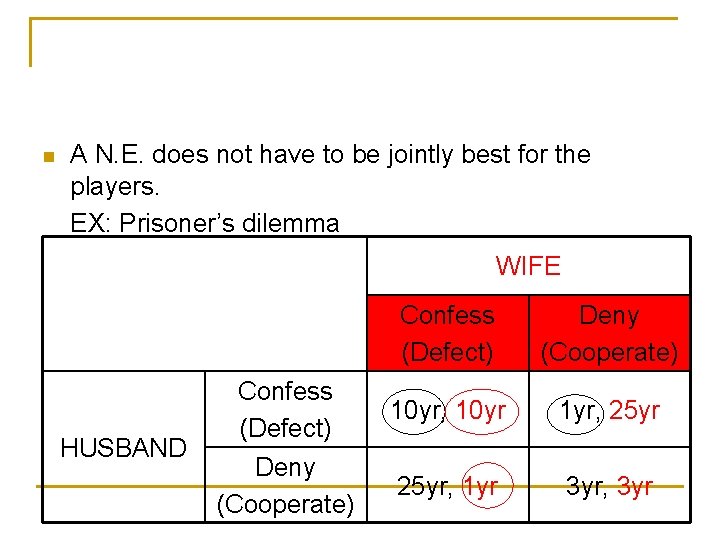
n A N. E. does not have to be jointly best for the players. EX: Prisoner’s dilemma WIFE HUSBAND Confess (Defect) Deny (Cooperate) 10 yr, 10 yr 1 yr, 25 yr, 1 yr 3 yr, 3 yr

n Nash Equilibrium as a system of beliefs n Nash Equilibrium is a set of strategies, such that (1)each player has correct beliefs about the strategies of the others (2)the strategy of each is the best for herself, given her beliefs about the strategies of the others

Dominance HUSBAND n Confess (Defect) Deny (Cooperate) WIFE Confess (Defect) Deny (Cooperate) 10 yr, 10 yr 1 yr, 25 yr, 1 yr 3 yr, 3 yr Dominant strategy is an action clearly best for a player, no matter what the others might be doing. n“Confess” is a dominant strategy for the husband, while “Confess” is also a dominant strategy for the wife. NE: (Confess, Confess) →(10 yr, 10 yr)

n n (A, B, …. . ) are strategies for Player 1. A is a dominant strategy for Player 1. A dominates B/C/D… is a dominated strategy for Player 1.

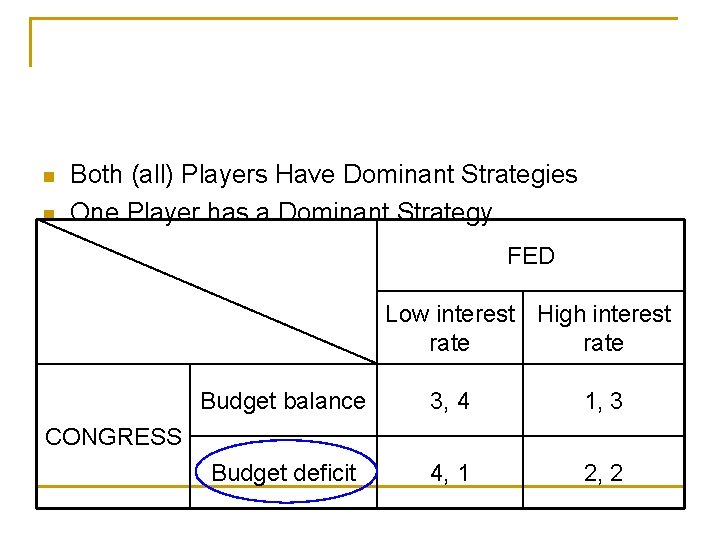
n n Both (all) Players Have Dominant Strategies One Player has a Dominant Strategy FED Low interest High interest rate Budget balance 3, 4 1, 3 Budget deficit 4, 1 2, 2 CONGRESS

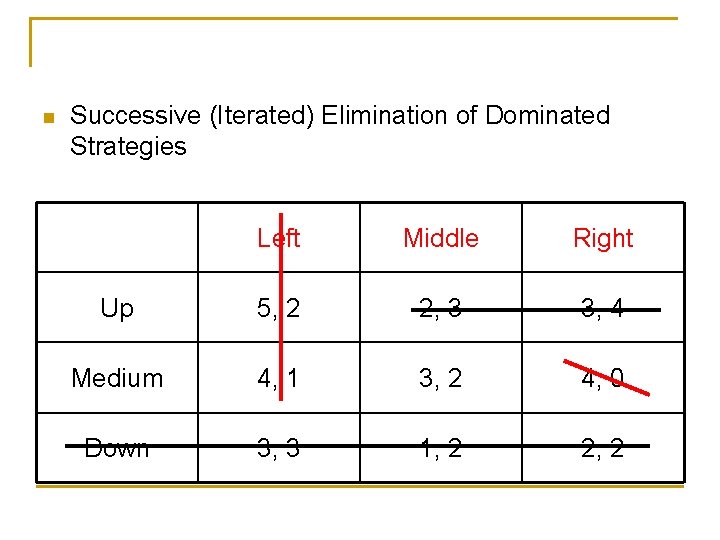
n Successive (Iterated) Elimination of Dominated Strategies Left Middle Right Up 5, 2 2, 3 3, 4 Medium 4, 1 3, 2 4, 0 Down 3, 3 1, 2 2, 2

Mini. Max Method for Zero-Sum Games n Mini. Max/Maximin Column OFFENSE Run Pass Blitz Run 2 5 13 Short Pass 6 5. 6 10. 5 Medium Pass 6 4. 5 1 Long Pass 10 3 -2

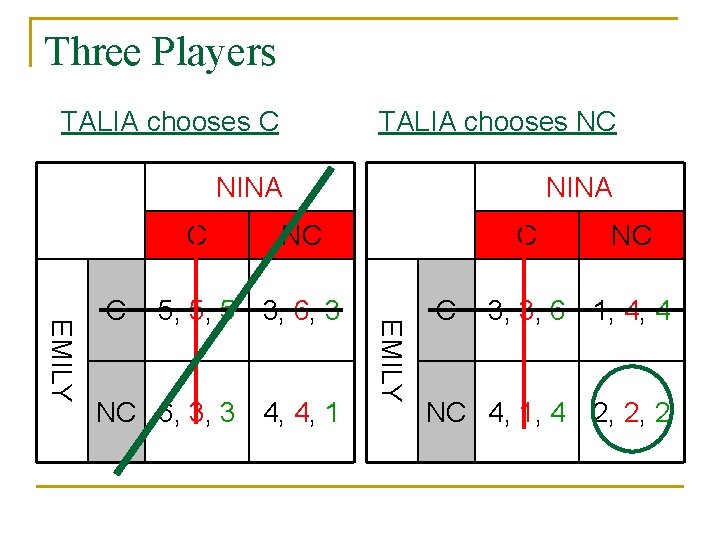
Three Players TALIA chooses C TALIA chooses NC NINA C 5, 5, 5 3, 6, 3 NC 6, 3, 3 4, 4, 1 C EMILY C NC 3, 3, 6 1, 4, 4 NC 4, 1, 4 2, 2, 2

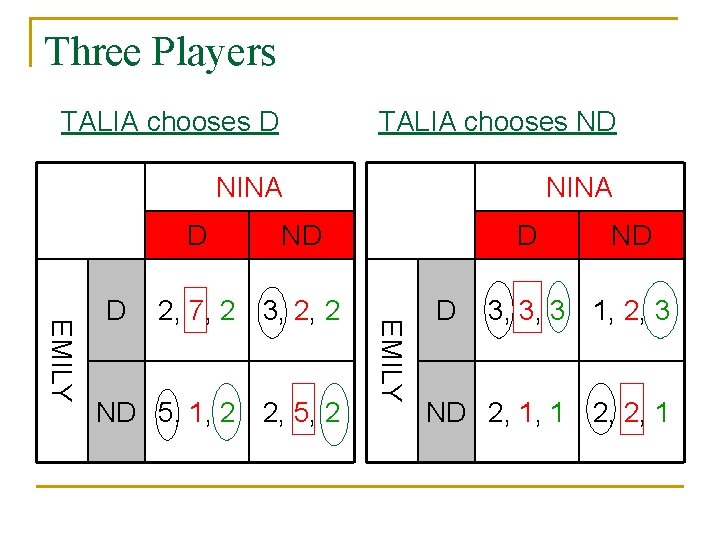
Three Players TALIA chooses D TALIA chooses ND NINA D 2, 7, 2 3, 2, 2 ND 5, 1, 2 2, 5, 2 D EMILY D ND 3, 3, 3 1, 2, 3 ND 2, 1, 1 2, 2, 1

Multiple Equilibria in Pure Strategies n n Coordination Games Battle of the Sexes SALLY Starbucks Banyan Starbucks 2, 1 0, 0 Banyan 0, 0 1, 2 HARRY

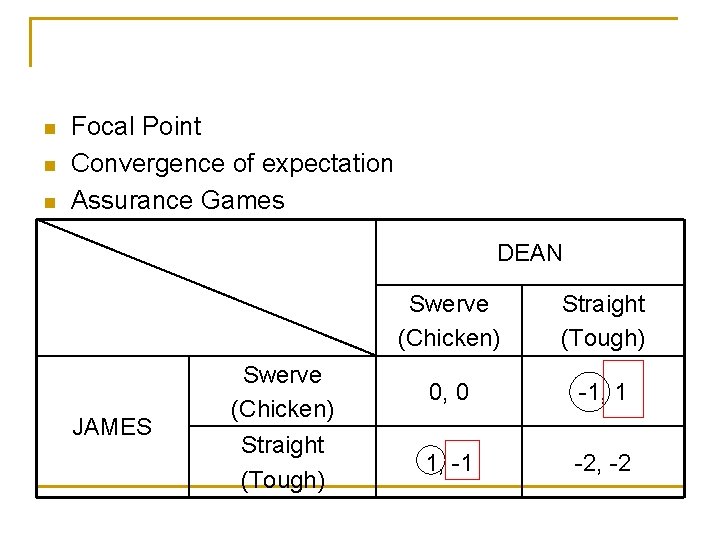
n n n Focal Point Convergence of expectation Assurance Games DEAN JAMES Swerve (Chicken) Straight (Tough) Swerve (Chicken) 0, 0 -1, 1 Straight (Tough) 1, -1 -2, -2

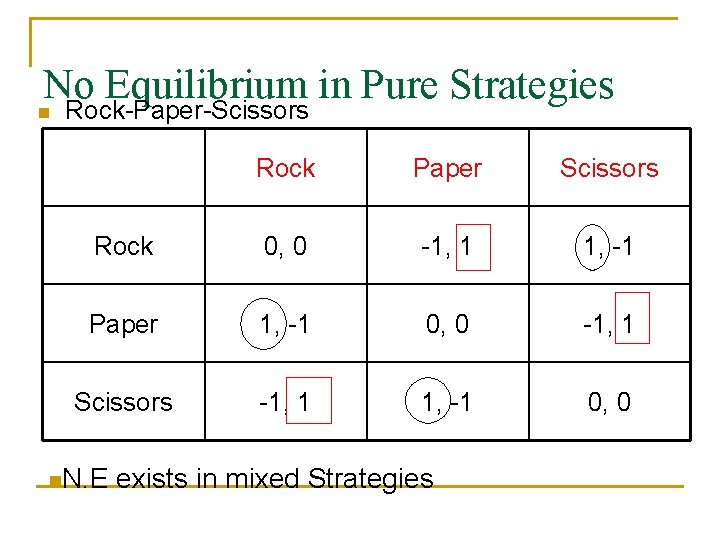
No Equilibrium in Pure Strategies n Rock-Paper-Scissors Rock Paper Scissors Rock 0, 0 -1, 1 1, -1 Paper 1, -1 0, 0 -1, 1 Scissors -1, 1 1, -1 0, 0 n. N. E exists in mixed Strategies

n n Homework, Ch 4 question 3, 6, 11, and 12(a & b)

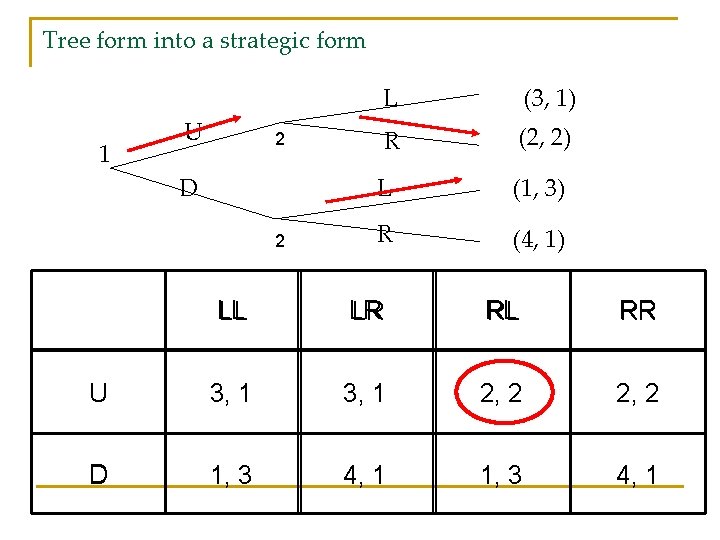
Tree form into a strategic form 1 U 2 D 2 L (3, 1) R (2, 2) L (1, 3) R (4, 1) LL LR LR RL RR U 3, 1 2, 2 D 1, 3 4, 1

n Minimax/Maximin vs. Nash Equilibrium Revisited