Game Trees Ryan Wilson Chapter 6 Trees A

Game Trees Ryan Wilson Chapter 6

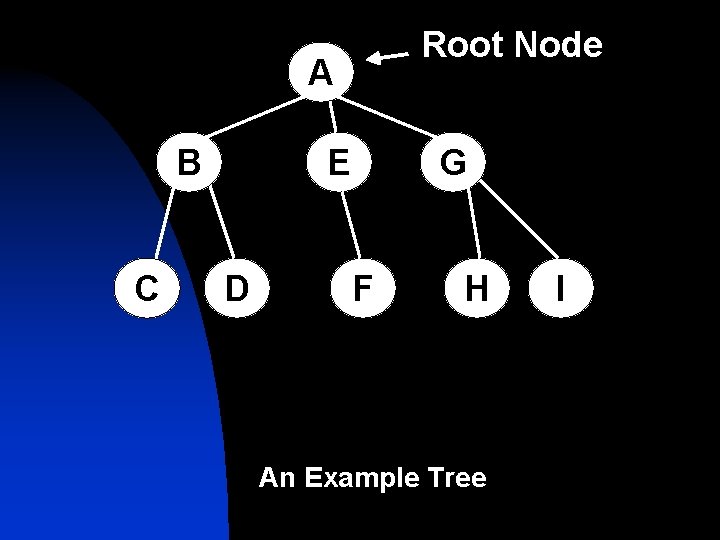
Trees – A Review n n Trees are a collection of nodes A Tree has a root node and zero or more sub-trees

Root Node A B C E D G F H An Example Tree I

Common Traversal Algorithm Function Traverse. Tree( node ) visit( node ) for each child of node Traverse. Tree( child ) end for End Function Traverse. Tree( root )

Computer Games n n Problem: How do we make an intelligent opponent for a human player to compete against? One Possibility: u Game Trees

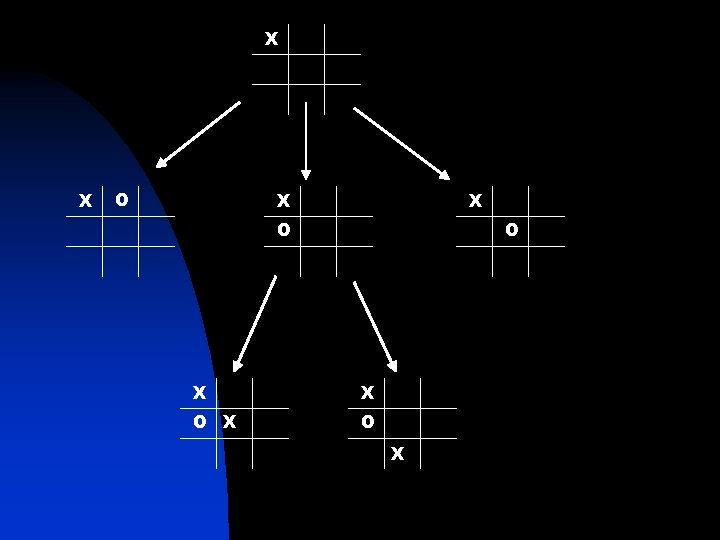
Game Trees n n Treat each state of the game as a node in a tree Search the tree to find the best move

X X O O X X O X

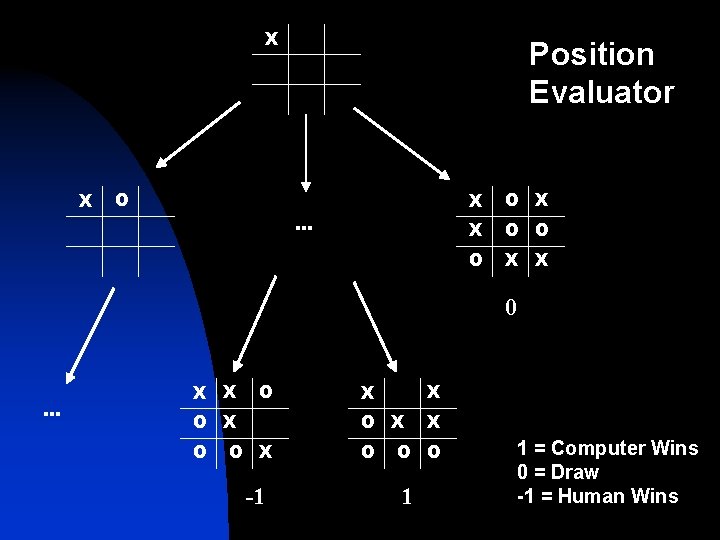
Game Trees n 3 Components to Implementing a Game Tree: Tree Generator u Position Evaluator u Minimax Method u

X X O Position Evaluator … X O X X O O O X X 0 … X X O X O X X O O O X -1 O O 1 1 = Computer Wins 0 = Draw -1 = Human Wins

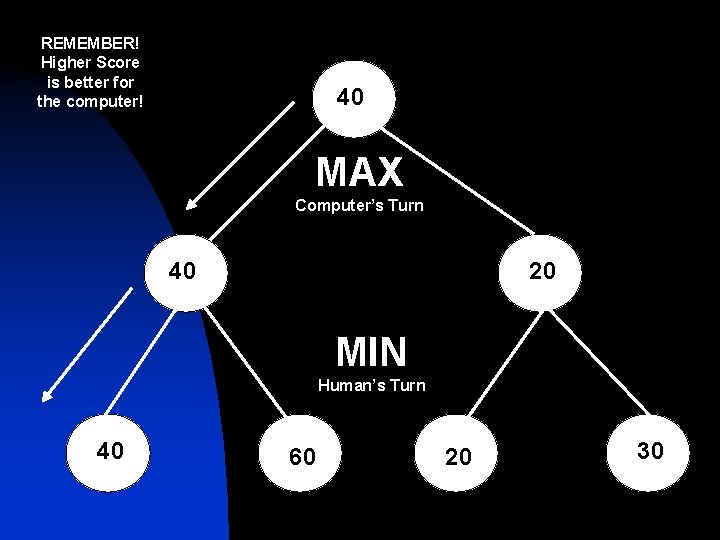
REMEMBER! Higher Score is better for the computer! 40 MAX Computer’s Turn 40 20 MIN Human’s Turn 40 60 20 30

Minimax - Computer Function Find. Computer. Move(Game. State. Node) var best. Value if( terminal ) return evaluate(Game. State. Node) for each child of Game. State. Node value = Find. Human. Move(child) if( value > best. Value ) best. Value = value end for End function

Minimax - Human Function Find. Human. Move(Game. State. Node) var best. Value if( terminal ) return evaluate(Game. State. Node) for each child of Game. State. Node value = Find. Human. Move(child) if( value < best. Value ) best. Value = value end for End function

Demonstration n Tic-Tac-Toe!

Conclusions n In Tic-Tac-Toe, there’s only about 27 legal moves for the computer to consider u n n That’s about 30, 000 moves But it’s still kind of slow… Almost 45 seconds to make the first move! Experts estimate 10100 legal moves in Chess! That’s approx. 2333 legal positions!

What can we do? n Apply the position evaluator to non-terminal nodes Limit the depth of your search through the tree u Have to estimate the value of a position u n Alpha-Beta Pruning u n “Trim” un-needed portions of the tree Transposition Tables

Alpha-Beta Pruning n Don’t need to look at all subtrees of a given node if you can already know which one is best

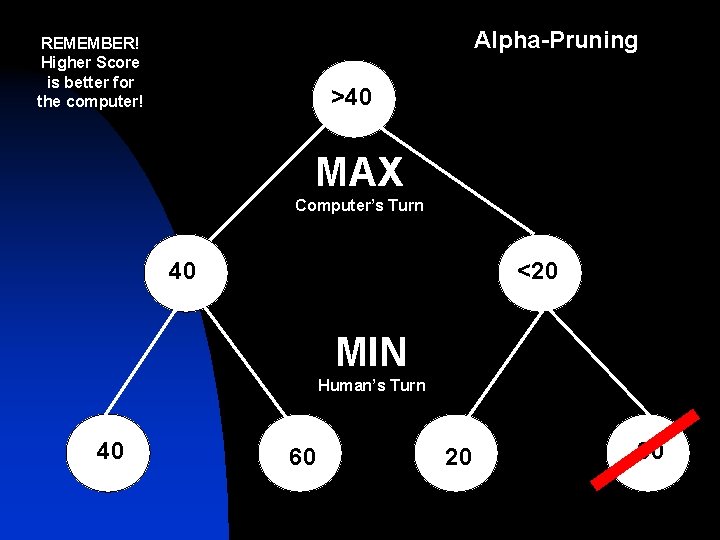
Alpha-Pruning REMEMBER! Higher Score is better for the computer! >40 MAX Computer’s Turn 40 <20 MIN Human’s Turn 40 60 20 30

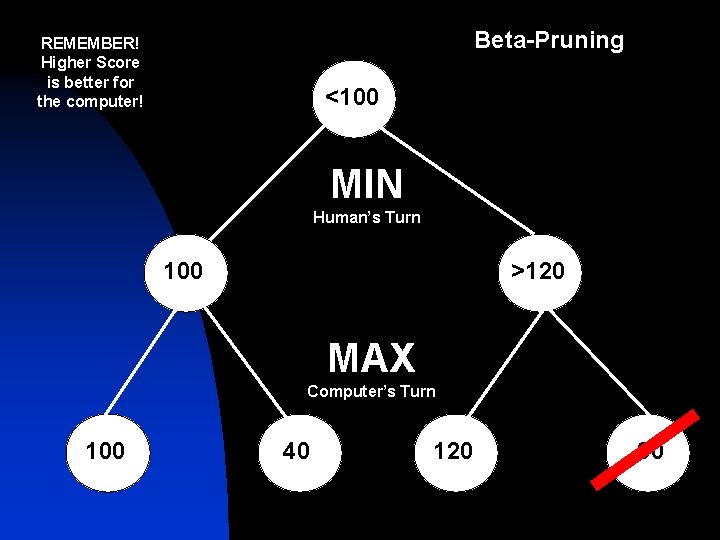
Beta-Pruning REMEMBER! Higher Score is better for the computer! <100 MIN Human’s Turn 100 >120 MAX Computer’s Turn 100 40 120 30

Demonstration n Tic-Tac-Toe! u With Alpha-Beta Pruning

Conclusions n n A definite improvement! First move only takes about 4 seconds (about 2000 moves)

Transposition Tables n In many games, there are multiple ways to arrive at the same board position…

X X X O O X X O X

Transposition Tables n n Once we’ve calculated the value of a given position, we save it in a table so it’s easy to look up. For each position in the tree, look that position up in the table, if it exists, return the value stored in the table.

Demonstration n Tic-Tac-Toe! With Alpha-Beta Pruning u With Transposition Tables u

Conclusions n n n Another improvement! First move only takes about 3 seconds (918 nodes) Almost ½ as many nodes!

Game Trees n n n How-To of Game Trees Alpha-Beta Pruning Transposition Tables

References n n n Dewdney The New Turing Omnibus Weiss Algorithms, Data Structures, and Problem Solving with C++ Weiss Data Structures & Algorithm Analysis in C++