GAME THEORY STRATEGIC DECISION MAKING Strategic Normal Form

GAME THEORY STRATEGIC DECISION MAKING

Strategic (Normal) Form Games Static Games of Complete and Imperfect Information

What is a Normal Form Game? A normal (strategic) form game consists of: w Players: list of players w Strategies: all actions available to all players w Payoffs: a payoff assigned to every contingency (every possible strategy profile as the outcome of the game)

Prisoners’ Dilemma w Two suspects are caught and put in different rooms (no communication). They are offered the following deal: – If both of you confess, you will both get 5 years in prison (-5 payoff) – If one of you confesses whereas the other does not confess, you will get 0 (0 payoff) and 10 (-10 payoff) years in prison respectively. – If neither of you confess, you both will get 2 years in prison (-2 payoff)

Easy to Read Format of Prisoner’s Dilemma Prisoner 2 Prisoner 1 Confess Don’t Confess -5, -5 0, -10, 0 -2, -2

Assumptions in Static Normal Form Games w All players are rational. w Rationality is common knowledge. w Players move simultaneously. (They do not know what the other player has chosen). w Players have complete but imperfect information.

Solution of a Static Normal Form Game w Equilibrium in strictly dominant strategies – A strictly dominant strategy is the one that yields the highest payoff compared to the payoffs associated with all other strategies. – Rational players will always play their strictly dominant strategies.

Solution of a Static Normal Form Game w Iterated elimination of strictly dominated strategies – Rational players will never play their dominated strategies. – Eliminating dominated strategies may solve the game.

Solution of a Static Normal Form Game (cont. ) w Nash Equilibrium (NE): – In equilibrium neither player has an incentive to deviate from his/her strategy, given the equilibrium strategies of rival players. – Neither player can unilaterally change his/her strategy and increase his/her payoff, given the strategies of other players.

Definition of Nash Equilibrium w A strategy profile is a list (s 1, s 2, …, sn) of the strategies each player is using. w If each strategy is a best response given the other strategies in the profile, the profile is a Nash equilibrium. w Why is this important? – If we assume players are rational, they will play Nash strategies. – Even less-than-rational play will often converge to Nash in repeated settings.

An Example of a Nash Equilibrium Column a b a 1, 2 0, 1 b 2, 1 1, 0 Row (b, a) is a Nash equilibrium. To prove this: Given that column is playing a, row’s best response is b. Given that row is playing b, column’s best response is a.

Finding Nash Equilibria – Dominated Strategies w What to do when it’s not obvious what the equilibrium is? w In some cases, we can eliminate dominated strategies. – These are strategies that are inferior for every opponent action. w In the previous example, row = a is dominated.

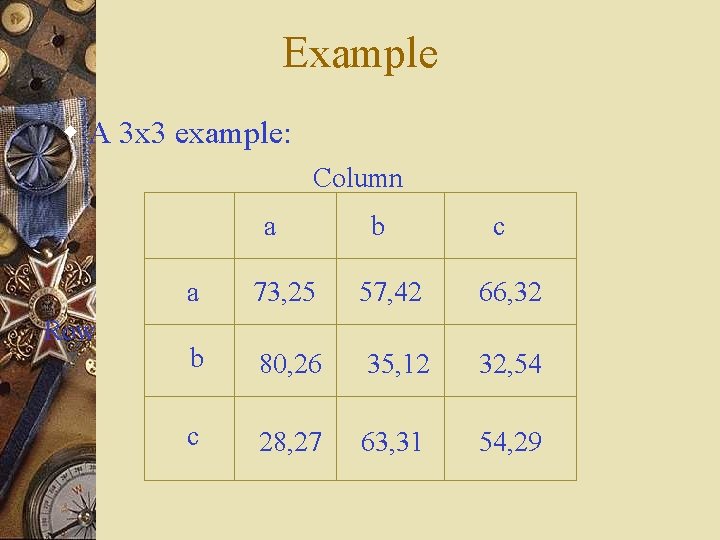
Example w A 3 x 3 example: Column a Row b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29

Example w A 3 x 3 example: Column a Row b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29 c dominates a for the column player

Example w A 3 x 3 example: Column a Row b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29 b is then dominated by both a and c for the row player.

Example w A 3 x 3 example: Column a Row b 57, 42 c a 73, 25 66, 32 b 80, 26 35, 12 32, 54 c 28, 27 63, 31 54, 29 Given this, b dominates c for the column player – the column player will always play b.

Solution of Prisoners’ Dilemma Dominant Strategy Equilibrium Prisoner 2 Prisoner 1 Confess Don’t Confess -5, -5 0, -10 Don’t Confess -10, 0 -2, -2

Solution of Prisoners’ Dilemma Iterated Elimination Procedure Prisoner 2 Prisoner 1 Confess Don’t Confess -5, -5 0, -10 Don’t Confess -10, 0 -2, -2

Solution of Prisoners’ Dilemma Cell-by-cell Inspection Prisoner 2 Prisoner 1 Confess Don’t Confess -5, -5 0, -10 Don’t Confess -10, 0 -2, -2

NE of Prisoners’ Dilemma w The strategy profile {confess, confess} is the unique pure strategy NE of the game. w In equilibrium both players get a payoff of – 5. w Inefficient equilibrium; (don’t confess, don’t confess) yields higher payoffs for both.

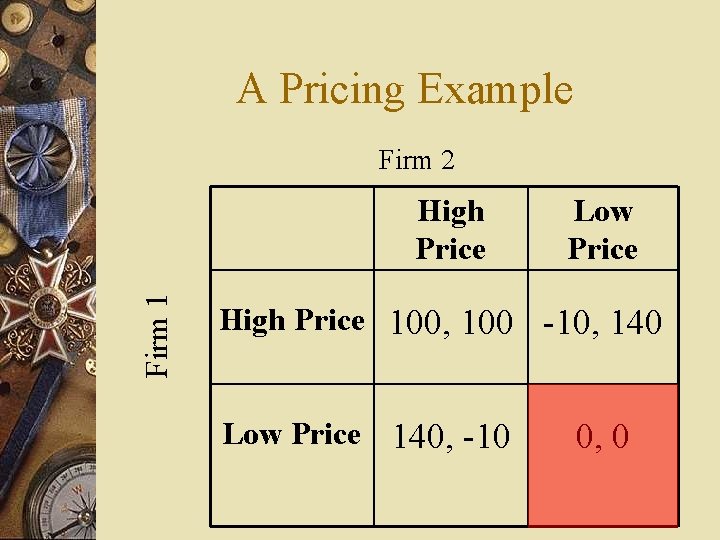
A Pricing Example Firm 2 Firm 1 High Price Low Price High Price 100, 100 -10, 140 Low Price 140, -10 0, 0

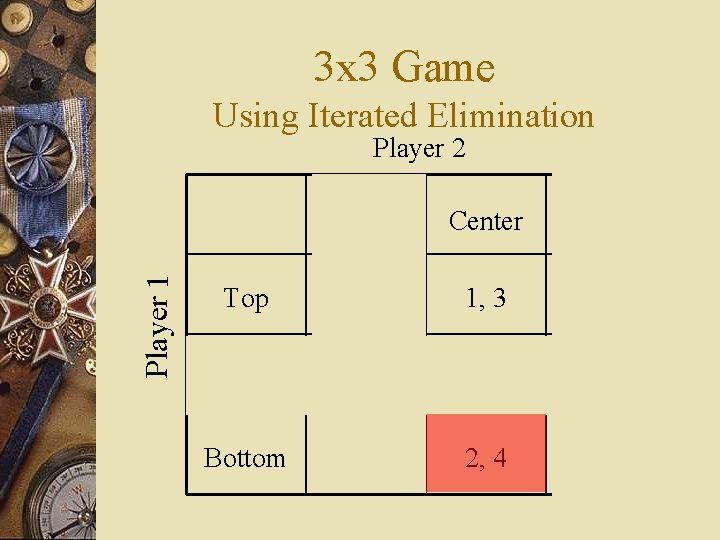
3 x 3 Game Using Iterated Elimination Player 1 Player 2 Left Center Right Top 1, 0 1, 3 3, 0 Middle 0, 2 0, 1 3, 0 Bottom 0, 2 2, 4 5, 3

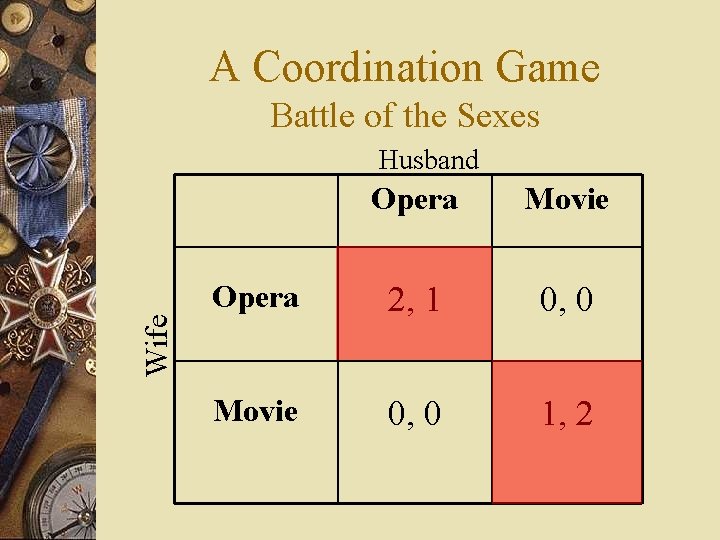
A Coordination Game Battle of the Sexes Husband Movie Opera 2, 1 0, 0 Movie 0, 0 1, 2 Wife Opera

Battle of the Sexes: After 30 Years of Marriage Wife Husband Opera Movie Opera 3, 2 0, 0 Movie 0, 0 1, 2

Mixed strategies w Unfortunately, not every game has a pure strategy equilibrium. – Rock-paper-scissors w However, every game has a mixed strategy Nash equilibrium. w Each action is assigned a probability of play. w Player is indifferent between actions, given these probabilities.

Mixed Strategies w In many games (such as coordination games) a player might not have a pure strategy. w Instead, optimizing payoff might require a randomized strategy (also called a mixed strategy) Wife football Husband shopping football 2, 1 0, 0 shopping 0, 0 1, 2

A Strictly Competitive Game Matching Pennies Player 2 Player 1 Heads Tails 1, -1 -1, 1 No NE in pure strategies -1, 1 1, -1

Extensive Form Games Dynamic Games of Complete and Perfect Information

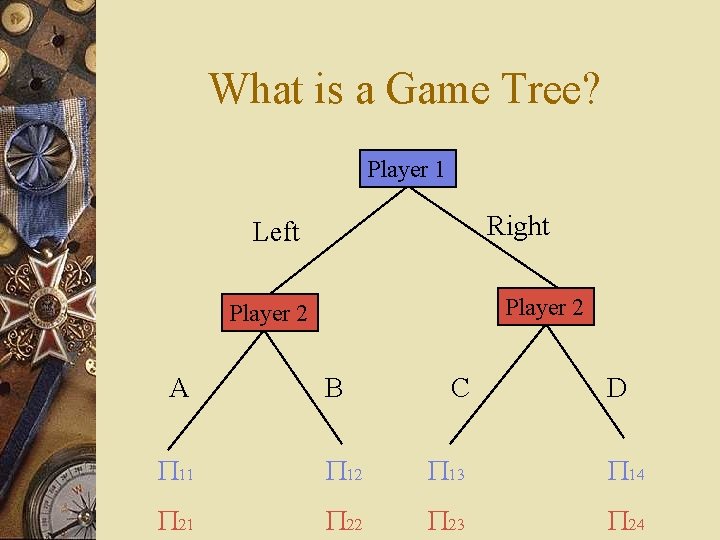
What is a Game Tree? Player 1 Right Left Player 2 A B C D P 11 P 12 P 13 P 14 P 21 P 22 P 23 P 24

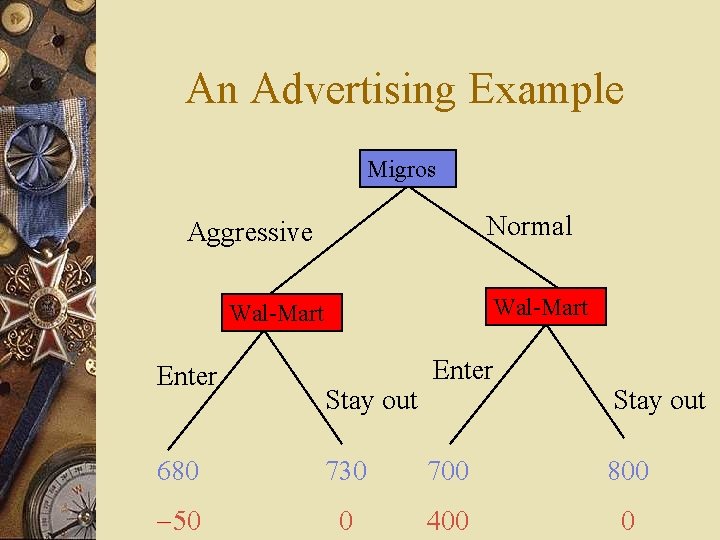
An Advertising Example Migros Normal Aggressive Wal-Mart Enter Stay out 680 730 700 800 -50 0 400 0

Assumptions in Dynamic Extensive Form Games w All players are rational. w Rationality is common knowledge w Players move sequentially. (Therefore, also called sequential games) w Players have complete and perfect information – Players can see the full game tree including the payoffs – Players can observe and recall previous moves

Solution of an Extensive Form Game w Subgame Perfect Equilibrium: For an equilibrium to be subgame perfect, it has to be a NE for all the subgames as well as for the entire game. – A subgame is a decision node from the original game along with the decision nodes and end nodes. – Backward induction is used to find SPE

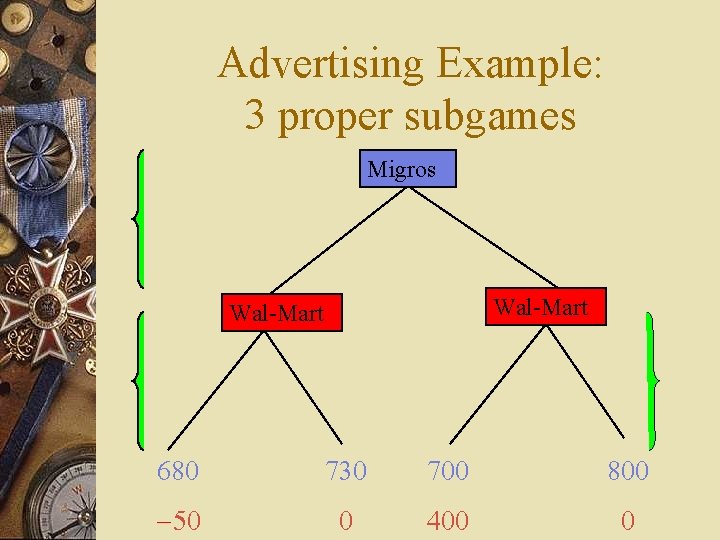
Advertising Example: 3 proper subgames Migros Wal-Mart 680 730 700 800 -50 0 400 0

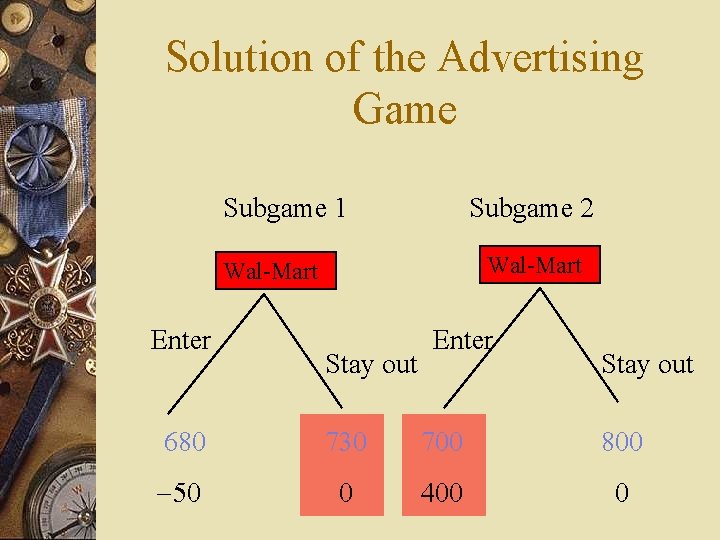
Solution of the Advertising Game Subgame 1 Subgame 2 Wal-Mart Enter Stay out 680 730 700 800 -50 0 400 0

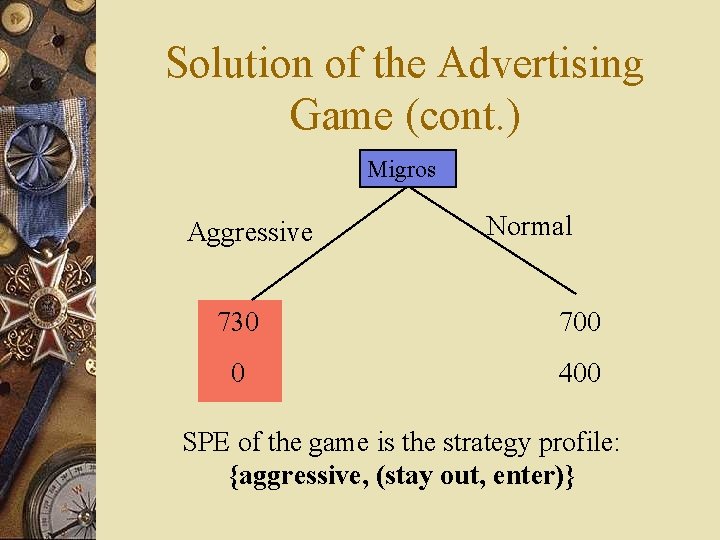
Solution of the Advertising Game (cont. ) Migros Aggressive Normal 730 700 0 400 SPE of the game is the strategy profile: {aggressive, (stay out, enter)}

Properties of SPE w The outcome that is selected by the backward induction procedure is always a NE of the game with perfect information. w SPE is a stronger equilibrium concept than NE w SPE eliminates NE that involve incredible threats.

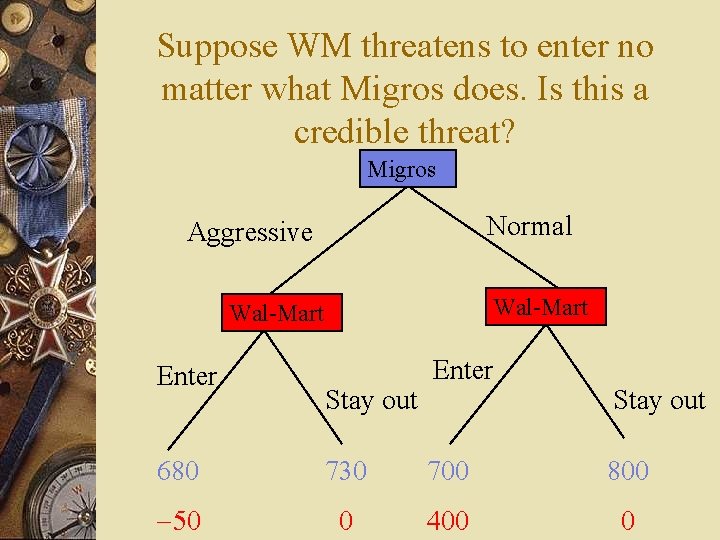
Suppose WM threatens to enter no matter what Migros does. Is this a credible threat? Migros Normal Aggressive Wal-Mart Enter Stay out 680 730 700 800 -50 0 400 0