Game Theory in Wireless and Communication Networks Theory

Game Theory in Wireless and Communication Networks: Theory, Models, and Applications Lecture 14 Mean-Field Game Zhu Han, Dusit Niyato, Walid Saad, and Tamer Basar Thanks for Dr. Chungang Yang slides • 1

Overview of Lecture Notes l Introduction to Game Theory: Lecture 1, book 1 l Non-cooperative Games: Lecture 1, Chapter 3, book 1 l Bayesian Games: Lecture 2, Chapter 4, book 1 l Differential Games: Lecture 3, Chapter 5, book 1 l Evolutionary Games: Lecture 4, Chapter 6, book 1 l Cooperative Games: Lecture 5, Chapter 7, book 1 l Auction Theory: Lecture 6, Chapter 8, book 1 l Matching Game: Lecture 7, Chapter 2, book 2 l Contract Theory, Lecture 8, Chapter 3, book 2 l Learning in Game, Lecture 9, Chapter 6, book 2 l Stochastic Game, Lecture 10, Chapter 4, book 2 l Game with Bounded Rationality, Lecture 11, Chapter 5, book 2 l Equilibrium Programming with Equilibrium Constraint, Lecture 12, Chapter 7, book 2 l Zero Determinant Strategy, Lecture 13, Chapter 8, book 2 l Mean Field Game, Lecture 14, UCLA course l Network Economy, Lecture 15, Dr. Jianwei Huang, [2]

Outline n Basics of MFG n Applications of MFG n q Conventional MFG in Ultra-Dense D 2 D Communications q Ultra-Dense Small Cell Networks: MFG with Interference Dominator q Mean Field Game-Theoretic Learning Conclusion • 3

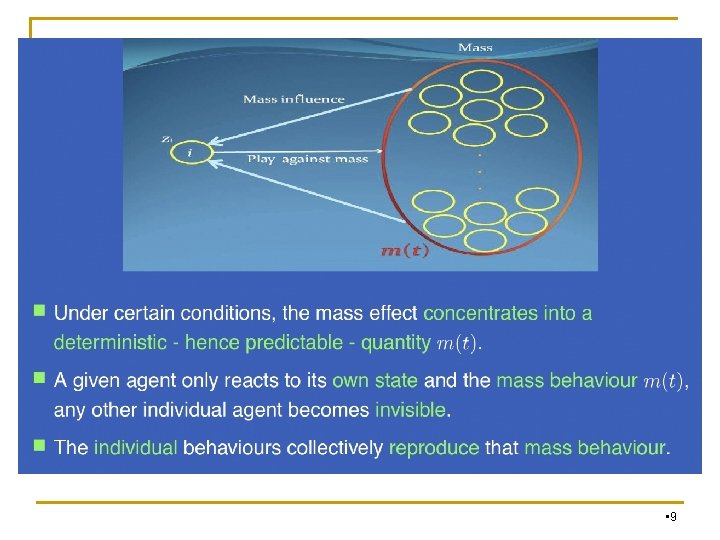
Mean Field Game, MFG n Basic Idea: While classical game theory models the interaction of a single player with all the other players of the system, a mean field game models the individual's interaction with the effect of the collective behavior of the players. Think individually while behave locally Think globally while locally • 4

Mean Field Game, MFG n Understand rational behaviors, and optimize their position in space and time dynamics. n The mean field theory is exploited to help decouple a complex large-scale optimization problem into a family of localized optimization problems. n Thus, each player can implement its policy by using only its local information. • 5

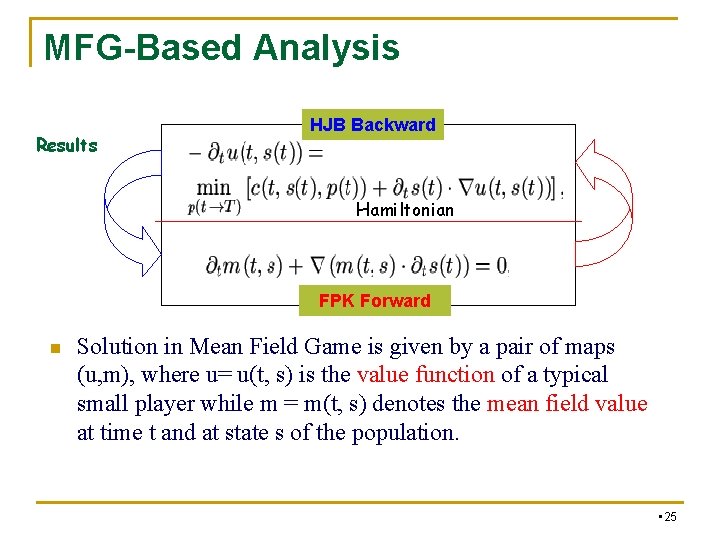
Mean Field Game, MFG n Mean Field Game describes equilibrium configurations and dynamic behaviors of huge number of homogeneous agents, which is a class of differential games in which each agent is infinitesimal and interacts with a huge population of other agents. n Solution in Mean Field Game is given by a pair of maps (u, m), where u= u(t, x) is the value function of a typical small player while m = m(t, x) denotes the mean field value at time t and at position x of the population. • 6

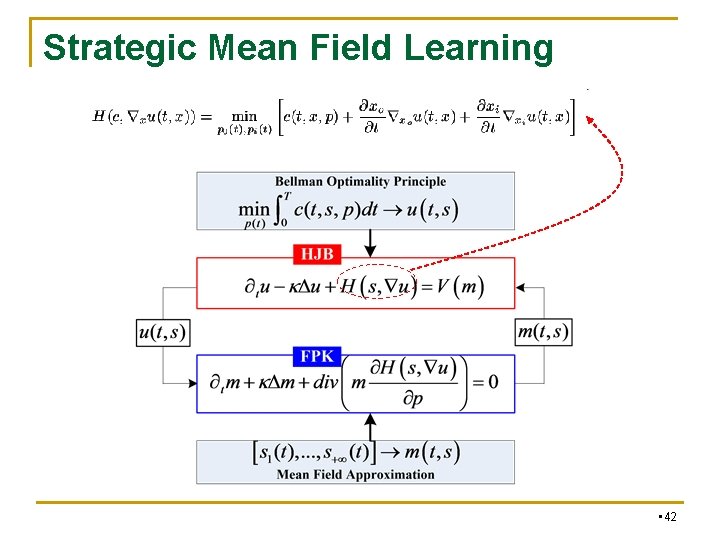
Mean Field Game, MFG n n The value function u satisfies a Hamilton-Jacobi-Bellman (HJB) equation—in which m enters as a parameter and describes the influence of the population on the cost of each agent, while the density m evolves in time according to a Fokker-Planck-Kolmogorov (FPK) equation in which u enters as a drift. More precisely the pair (u, m) is a solution of the MFG system. • 7

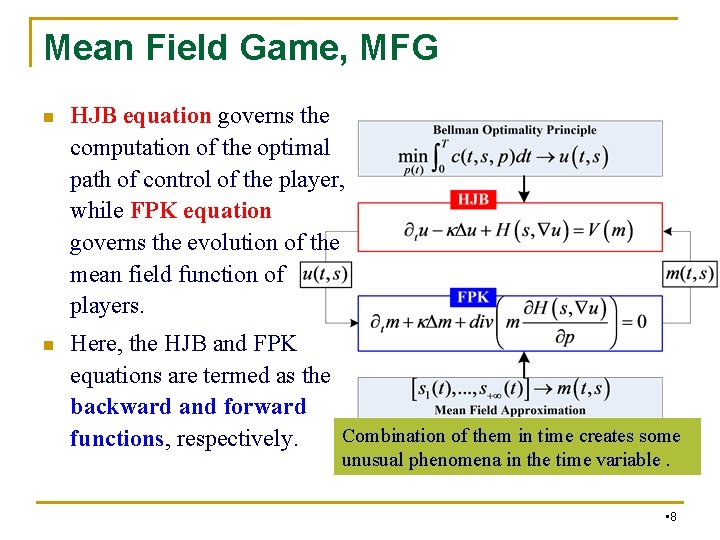
Mean Field Game, MFG n HJB equation governs the computation of the optimal path of control of the player, while FPK equation governs the evolution of the mean field function of players. n Here, the HJB and FPK equations are termed as the backward and forward Combination of them in time creates some functions, respectively. unusual phenomena in the time variable. • 8

Outline n Basics of MFG n Applications of MFG n q Conventional MFG in Ultra-Dense D 2 D Communications q Ultra-Dense Small Cell Networks: MFG with Interference Dominator q Mean Field Game-Theoretic Learning Conclusion • 10

Challenges in 5 G Ultra-Dense Networks n Io. E: Internet of Everything n Mobile Internet n q 5 G Ultra-Dense Small Cells q Social-Aware D 2 D Networks Internet of Things q n M 2 M, V 2 V Networks 5 G Characteristics: Ultra-Dense, Scalable, Self-Organizing; Energy efficiency, spectral efficiency, cost efficiency • 11

Challenges in 5 G Ultra-Dense Networks n n Technical Challenges q Coupled Systems & Interference -Limited Resources q Computationally Intractable & Analysis –Number Infinity q Low Convergence Rate & Robustness -Dynamics q Perfect Information & Backhauling Overhead -Others Requirements q Self-Organization & Distributed Control q Space-time Dynamics • 12

Game Theory in 5 G Era n Extensive applications to characterize the rational behaviors, model the strategic interactions, and design distributed algorithms. n Face great challenges, e. g. , the number of the nodes, e. g. , access points and small cell base stations, is huge, even goes to infinity, leading to the well-known curse of dimensionality. Hard to analyze the game due to the involved dynamics, complexity, interaction, signaling overhead, and so on. n • 13

Applications of MFG in Wireless Networks n n n Green Communications and Cognitive Radio Networks q H. Tembine, R. Tempone, and R. Vilanova, "Mean field games for cognitive radio networks", American Control Conference (ACC), Pages: 6388 -6393, 2012. q F. Meriaux and S. Lasaulce, "Mean-field games and green power control", 2011 5 th International Conference on Network Games, Control and Optimization (Net. GCoo. P), Pages: 1 -5, 2011. Hyper-Dense Heterogeneous Small Cell Networks q Prabodini Semasinghe and Ekram Hossain, Downlink Power Control in Self-Organizing Dense. Small Cells Underlaying Macrocells: A Mean Field Game, IEEE Transactions on Mobile Computing. q Ali Y. Al-Zahrani, F. Richard Yu, and Minyi Huang, A Joint Cross-Layer and Co-Layer Interference Management Scheme in Hyper-Dense Heterogeneous Networks Using Mean-Field Game Theory, IEEE Transactions on Vehicular Technology, 2015. Cloud and Smart V 2 V Networks q A. F. Hanif, H. Tembine, M. Assaad, and D. Zeghlache, "Mean-field games for resource sharing in cloud-based networks", IEEE/ACMTransactions on Networking, 2015. q R. Couillet, S. M. Perlaza, H. Tembine, and M. Debbah, "Electrical Vehicles in the Smart Grid-A Mean Field Game Analysis", IEEE Journal on Selected Areas in Communications, Publication Year: 2012 , Page(s): 1086 1096. • 14

n Distributed Interference and Energy Aware Power Control for Ultra-Dense D 2 D Networks: A Mean Field Game • 15

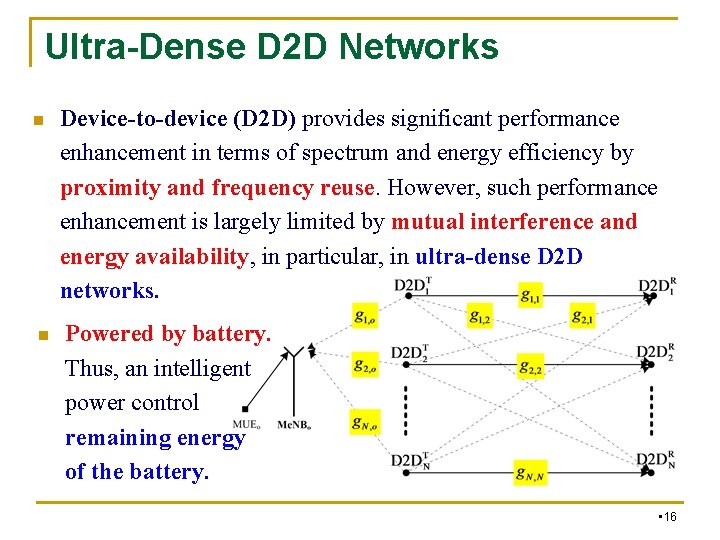
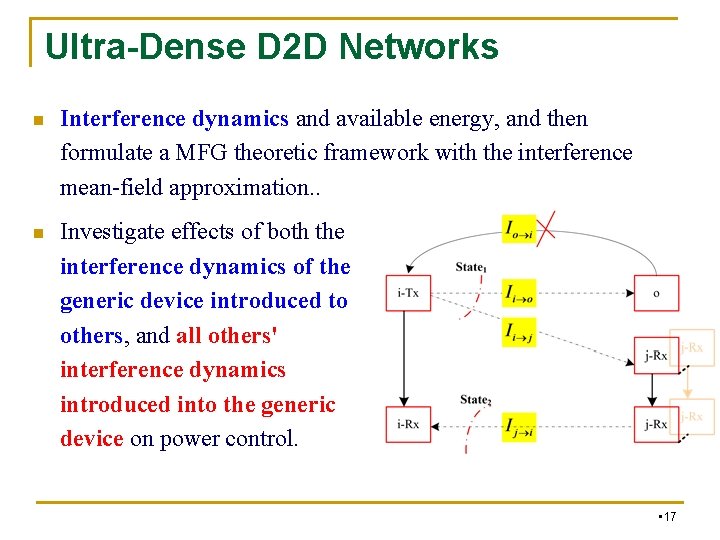
Ultra-Dense D 2 D Networks n n Device-to-device (D 2 D) provides significant performance enhancement in terms of spectrum and energy efficiency by proximity and frequency reuse. However, such performance enhancement is largely limited by mutual interference and energy availability, in particular, in ultra-dense D 2 D networks. Powered by battery. Thus, an intelligent power control remaining energy of the battery. • 16

Ultra-Dense D 2 D Networks n Interference dynamics and available energy, and then formulate a MFG theoretic framework with the interference mean-field approximation. . n Investigate effects of both the interference dynamics of the generic device introduced to others, and all others' interference dynamics introduced into the generic device on power control. • 17

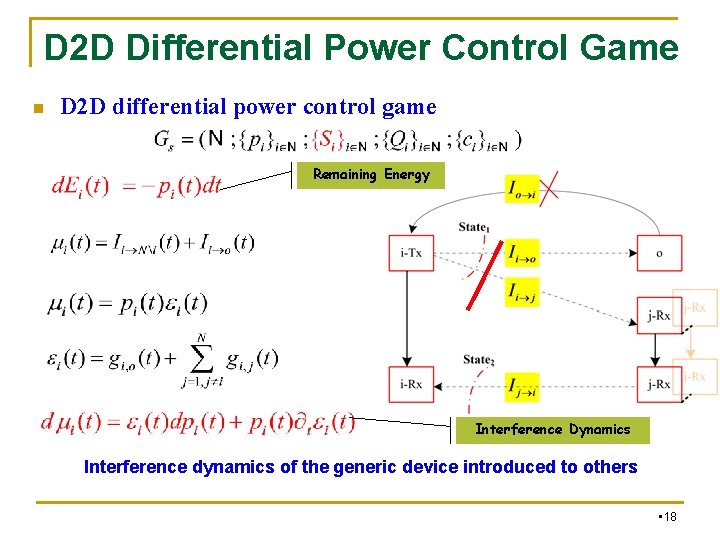
D 2 D Differential Power Control Game n D 2 D differential power control game Remaining Energy Interference Dynamics Interference dynamics of the generic device introduced to others • 18

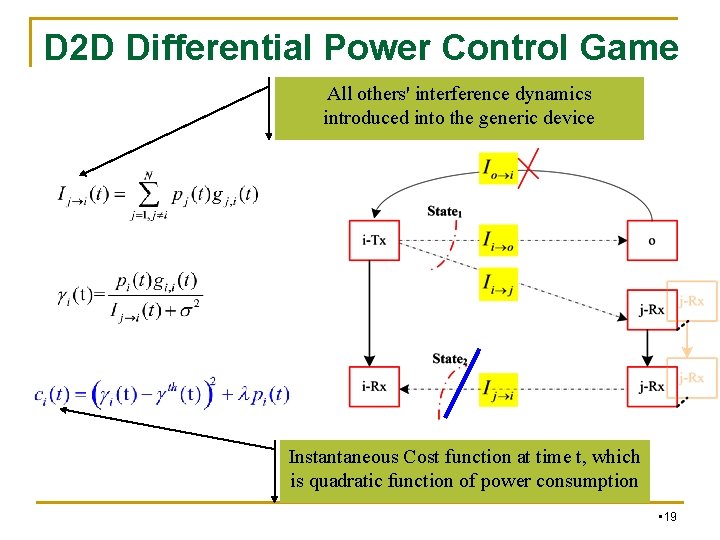
D 2 D Differential Power Control Game All others' interference dynamics introduced into the generic device Instantaneous Cost function at time t, which is quadratic function of power consumption • 19

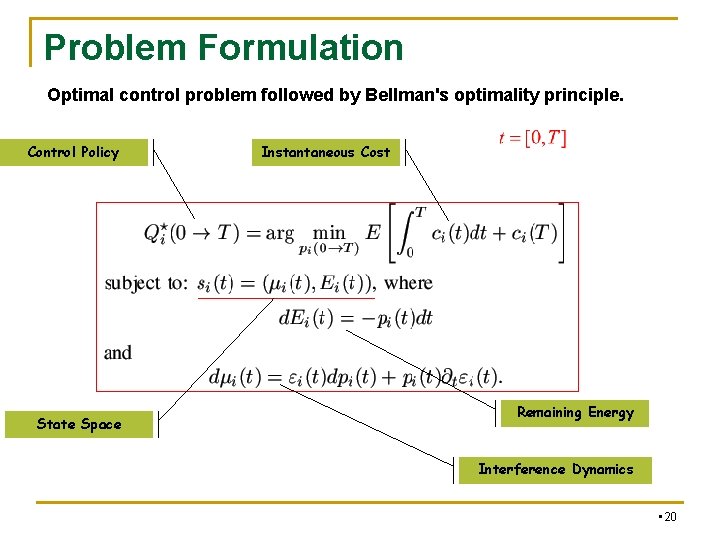
Problem Formulation Optimal control problem followed by Bellman's optimality principle. Control Policy State Space Instantaneous Cost Remaining Energy Interference Dynamics • 20

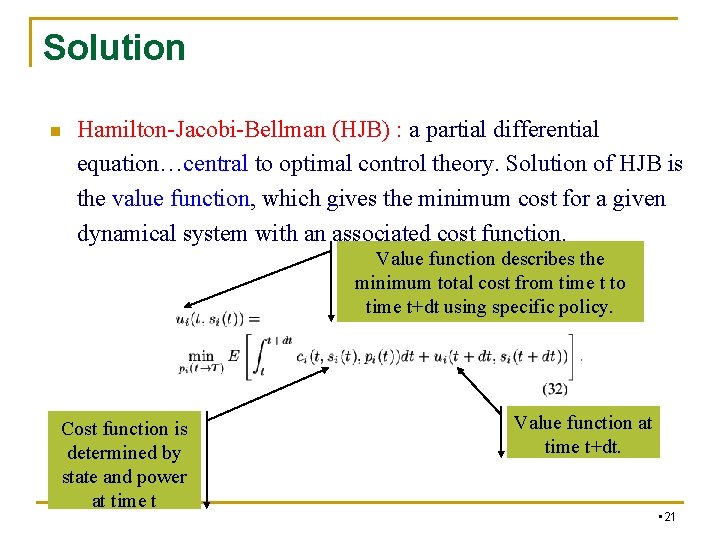
Solution n Hamilton-Jacobi-Bellman (HJB) : a partial differential equation…central to optimal control theory. Solution of HJB is the value function, which gives the minimum cost for a given dynamical system with an associated cost function. Value function describes the minimum total cost from time t to time t+dt using specific policy. Cost function is determined by state and power at time t Value function at time t+dt. • 21

Solution n Hamilton-Jacobi-Bellman (HJB) : • 22

Mean-Field Game n Obtaining equilibrium for a system with N players involves solving N simultaneous partial differential equations. n State Dynamics and Number of Players n Mean field n Fokker-Planck-Kolmogorov (FPK) equation • 23

Mean-Field Game n Mean field & FPK Equation • 24

MFG-Based Analysis Results HJB Backward Hamiltonian FPK Forward n Solution in Mean Field Game is given by a pair of maps (u, m), where u= u(t, s) is the value function of a typical small player while m = m(t, s) denotes the mean field value at time t and at state s of the population. • 25

MFG-Based Algorithm Finite difference Technique in discretized way of space Backward Forward • 26

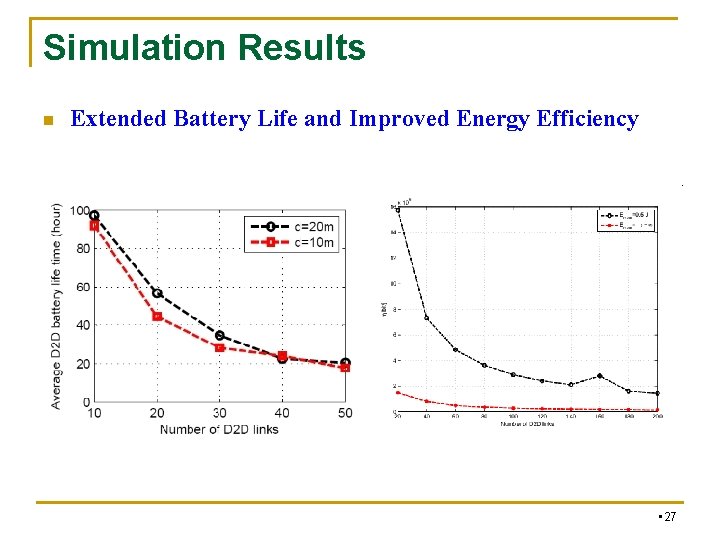
Simulation Results n Extended Battery Life and Improved Energy Efficiency • 27

n Distributed Interference Mitigation in Ultra-Dense Small Cell Networks: Mean Field Game with Interference Dominator • 28

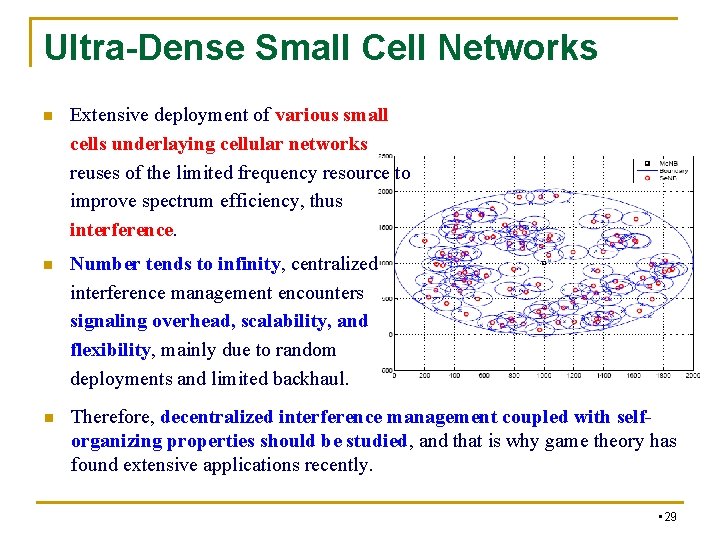
Ultra-Dense Small Cell Networks n Extensive deployment of various small cells underlaying cellular networks reuses of the limited frequency resource to improve spectrum efficiency, thus interference. n Number tends to infinity, centralized interference management encounters signaling overhead, scalability, and flexibility, mainly due to random deployments and limited backhaul. n Therefore, decentralized interference management coupled with selforganizing properties should be studied, and that is why game theory has found extensive applications recently. • 29

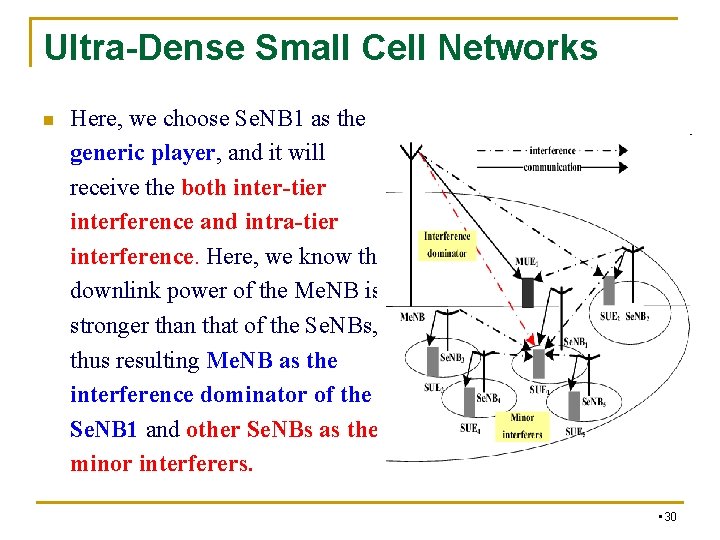
Ultra-Dense Small Cell Networks n Here, we choose Se. NB 1 as the generic player, and it will receive the both inter-tier interference and intra-tier interference. Here, we know the downlink power of the Me. NB is stronger than that of the Se. NBs, thus resulting Me. NB as the interference dominator of the Se. NB 1 and other Se. NBs as the minor interferers. • 30

Mean Field Game with Interference Dominator n We jointly take the global and individual perspective to react to the interference when the number of small cell players tends to infinity. n To analyze and characterize the equilibrium behaviors, we formulate it as a mean field game, which simplify the analysis and facilitate distributed interference mitigation. n To think globally while behave locally, in practice an interference dominator always exists in addition to the mean field term, which would significantly affects the decision-making for the representative agent. n Therefore, we turn to mean field games between a dominating player and a group of representative agents, each of which acts similarly and also interacts with each other through a mean field term being substantially influenced by the interference dominating player. • 31

Interference Mitigation Stochastic With tow kinds of players: Game Interference dominator and minor n Interference perceived by the interference dominator n Interference perceived by the minor generic interferer n Interference mean field: interferers • 32

Interference Mitigation Stochastic Game • 33

Interference Mitigation Stochastic Game • 34

MFG with Interference Dominator n We derive the HJB equation n We derive the FPK equation • 35

Solution n Mean Field Update • 36

Solution n Introduce Lagrangian Parameter to indirectly solve the HJB • 37

Solution n Power Update • 38

n Self-Confirming Interference Management Policy in 5 G Ultra-Dense Small Cell Networks: A Mean Field Game. Theoretic Learning Perspective • 39

Strategic Mean Field Learning n What is distributed strategic learning? n Distributed strategic learning is learning in the presence of other players (i. e. , from, with, or about others) or (from, with or about) Nature/ environment. n The term strategic learning stands for how the players can learn from/with/about the others (players, environment) under their complex strategies/beliefs. • 40

Strategic Mean Field Learning n The term mean field learning refers to a learning framework for large populations of players, which is highly related to HJB and/ or FPK equations. n Basically, we summarize that there exist two kinds of mean field learning techniques: q FPK forward equation, and mean field learning techniques q HJB backward equation, which relates to the Hamiltonian. • 41

Strategic Mean Field Learning • 42

Strategic Mean Field Learning n Huibing Yin; Mehta, P. G. ; Meyn, S. P. ; Shanbhag, U. V. , "Learning in Mean. Field Games, " in Automatic Control, IEEE Transactions on , vol. 59, no. 3, pp. 629 -644, March 2014 n Mehta, P. ; Meyn, S. , "Q-learning and Pontryagin's Minimum Principle, " in Decision and Control, 2009 held jointly with the 2009 28 th Chinese Control Conference. CDC/CCC 2009. Proceedings of the 48 th IEEE Conference on , vol. , no. , pp. 3598 -3605, 15 -18 Dec. 2009 • 43

Future Work n n n Working on: q Distributed Interference Mitigation in Ultra-Dense Small Cell Networks: Mean Field Game with Interference Dominator q Self-Confirming Interference Management Policy in 5 G Ultra -Dense Small Cell Networks: A Mean Field Game-Theoretic Learning Perspective Advanced MFG Framework: q Robust MFG q Cooperative MFG q …… New Applications: Io. T, Cloud, and Smart Gird; Various Techniques. • 44

Conclusion n Introduce the technical challenges in 5 G UDNs, which is the motivation of why we need MFG. After that, we introduce the basics of MFG framew ork. n Present a power control MFG in the ultra dense D 2 D networks, where our most important contribution is we jointly investigated the impacts of interference dynamics and remaining energy on the power control of a generic D 2 D player. n Present a interference mitigation MFG with interference dominator. C onsider interactive power control policies for both the dominator (Major pl ayer) and generic players (Minor players) in heterogeneous small cell UDN s. n Identify relation between the Qvalue and Hamiltonian. Thus, we turn to strategic MFG learning design. n Look forward our future work, and then conclude the presentation. • 45

Questions? • 46