Game Theory in Wireless and Communication Networks Theory

Game Theory in Wireless and Communication Networks: Theory, Models, and Applications Lecture 3 Differential Game Zhu Han, Dusit Niyato, Walid Saad, Tamer Basar, and Are Hjorungnes

Overview of Lecture Notes l Introduction to Game Theory: Lecture 1, book 1 l Non-cooperative Games: Lecture 1, Chapter 3, book 1 l Bayesian Games: Lecture 2, Chapter 4, book 1 l Differential Games: Lecture 3, Chapter 5, book 1 l Evolutionary Games: Lecture 4, Chapter 6, book 1 l Cooperative Games: Lecture 5, Chapter 7, book 1 l Auction Theory: Lecture 6, Chapter 8, book 1 l Matching Game: Lecture 7, book 2 l Contract Theory, Lecture 8, book 2 l Stochastic Game, Lecture 9, book 2 l Learning in Game, Lecture 10, book 2 l Equilibrium Programming with Equilibrium Constraint, Lecture 11, book 2 l Mean Field Game, Lecture 12, book 2 l Zero Determinant Strategy, Lecture 13, book 2 l Network Economy, Lecture 14, book 2 l Game in Machine Learning, Lecture 15, book 2 [2]

Introduction l Basics l Controllability l Linear ODE: Bang-bang control l Linear time optimal control l Pontryagin’s maximum principle l Dynamic programming l Dynamic game l Note: Some parts are not from the book. See some dynamic control book and Basar’s dynamic game book for more references. [3]

Basic Problem l ODE: x: state, f: a function, : control l Payoff: r: running payoff, g: terminal payoff [4]

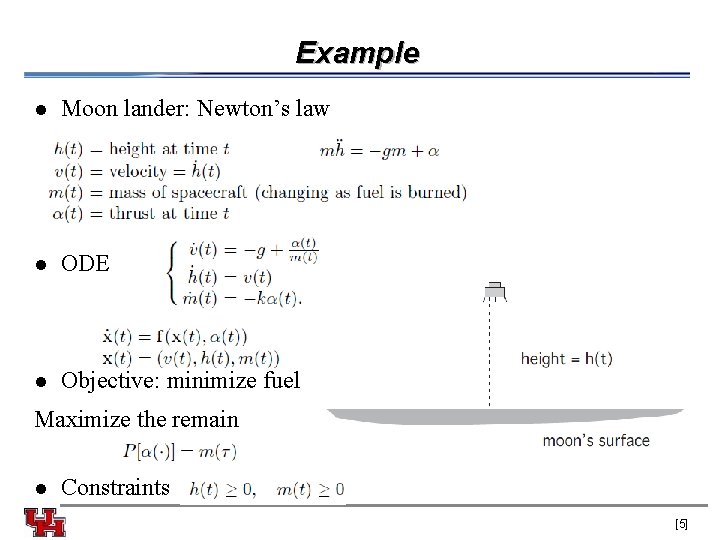
Example l Moon lander: Newton’s law l ODE l Objective: minimize fuel Maximize the remain l Constraints [5]

Controllability [6]

Linear ODE [7]

Controllability of Linear Equations [8]

Observability l Observation [9]

Bang-bang Control l Bang-bang control is optimal [10]

Existence Of Time-optimal Controls l Minimize the time from any point to the origin [11]

Maximum Principle For Linear System [12]

Hamiltonian l Definition [13]

Example: Rocket Railroad Car l x(t) = (q(t), v(t)) [14]

Example: Rocket Railroad Car Satellite example [15]

Pontryagin Maximum Principle l “The maximum principle was, in fact, the culmination of a long search in the calculus of variations for a comprehensive multiplier rule, which is the correct way to view it: p(t) is a “Lagrange multiplier”. . . It makes optimal control a design tool, whereas the calculus of variations was a way to study nature. ” [16]

Fixed Time, Free Endpoint Problem [17]

Pontryagin Maximum Principle adjoint equations maximization principle transversality condition [18]

Free Time, Fixed Endpoint Problem [19]

Pontryagin Maximum Principle [20]

Example: Linear-quadratic Regulator [21]

Introducing the Maximum Principle [22]

Using the Maximum Principle [23]

Riccati Equation [24]

Solving the Riccati Equation l Convert (R) into a second–order, linear ODE [25]

Dynamic Programming l “it is sometimes easier to solve a problem by embedding it in a larger class of problems and then solving the larger class all at once. ” [26]

Hamilton-Jacobi-Bellman Equation l “it’s better to be smart from the beginning, than to be stupid for a time and then become smart”. choice of life Backward induction: change to a sequence of constrained optimization [27]

Dynamic Programming Method [28]

Example: General Linear Quadratic Regulator [29]

HJB [30]

Minimization [31]

Minimization [32]

Minimization [33]

Relation between DP & Maximum Principle l Maximum principle starts from 0 to T l DP starts from t to T l Costate p at time t is the gradient [34]

Introduction l Basics l Controllability l Linear ODE: Bang-bang control l Linear time optimal control l Pontryagin’s maximum principle l Dynamic programming l Dynamic game [35]

Two-person, Zero-sum Differential Game l Basic idea: Two players control the dynamics of some evolving system, where one tries to maximize, and the other tries to minimize, a payoff functional that depends upon the trajectory [36]

Two-person, Zero-sum Differential Game [37]

Strategies l Idea: One player will select in advance, not his control, but rather his responses to all possible controls that could be selected by his opponent [38]

Value Functions [39]

Dynamic Programming, Isaacs’ Equations [40]

Dynamic Programming, Isaacs’ Equations [41]

Pontryagin’s Maximum Principle [42]

Non-cooperative Differential Game l Optimization problem for each player can be formulated as the optimal control problem l The dynamics of state variable and payoff of each player l For player to play the game, the available information is required l Three cases of available information 1. Open-loop information [43]

Non-cooperative Differential Game 2. Feedback information u u At time t, players are assumed to know the values of state variables at time where is positive and arbitrarily small The feedback information is defined as: 3. Closed-loop information l The Nash equilibrium is defined as a set of action paths of one player to maximize the payoff, given the other players' behavior [44]

Non-cooperative Differential Game l To obtain the Nash equilibrium, it is required to solve a dynamic optimization problem l The Hamiltonian function – where is co-state variable. Co-state variable is considered to be the shadow price of the variation of the state variable. [45]

Non-cooperative Differential Game l The first order conditions for the open-loop solution l For the closed-loop solution, the conditions are slightly different l Further reading: Basar’s book [46]

Summary of Dynamic Control l Dynamic problem formulation – ODE and payoff function l Conditions for controllability – Rank of G and eigenvalue of M l Bang-bang control l Maximum principle – ODE, ADJ, M and P l Dynamic programming – Divide a complicated problem into sequence of sub-problems – HJB equations l Dynamic game: Multiuser case l Future reading: Stochastic game [47]

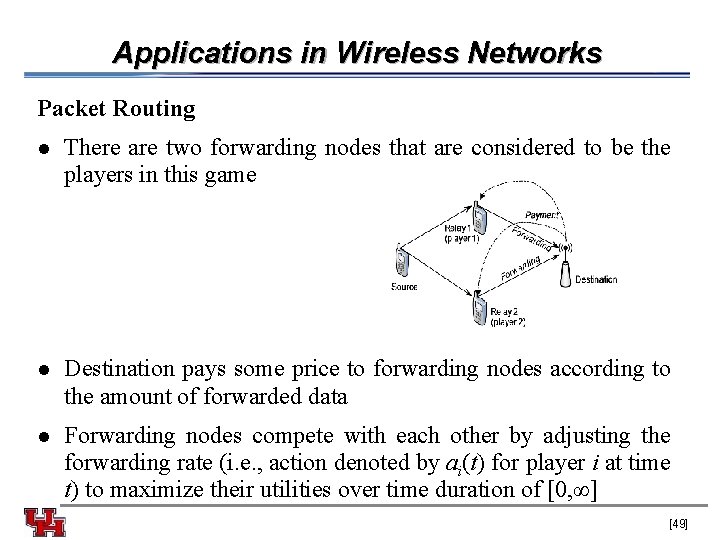
Applications in Wireless Networks Packet Routing l For routing in the mobile ad hoc network (MANET), the forwarding nodes as the players have incentive from the destination in terms of price to allocate transmission rate to forward packets from source l A differential game for duopoly competition is applied to model this competitive situation L. Lin, X. Zhou, L. Du, and X. Miao. Differential game model with coupling constraint for routing in ad hoc networks. In Proc. of the 5 th International Conference on Wireless Communications, Networking and Mobile Computing (Wi. COM 2009), pages 30423045, September 2009. [48]

Applications in Wireless Networks Packet Routing l There are two forwarding nodes that are considered to be the players in this game l Destination pays some price to forwarding nodes according to the amount of forwarded data l Forwarding nodes compete with each other by adjusting the forwarding rate (i. e. , action denoted by ai(t) for player i at time t) to maximize their utilities over time duration of [0, ∞] [49]

Applications in Wireless Networks Packet Routing l Payment from the destination at time t is denoted by P(t) l Payoff function of player i can be expressed as follows: - P(t)ai(t) is revenue Quadratic cost function - g(a) is a cost function given vector a of actions of players l For the payment, the following evolution of price (i. e. , a differential equation of Tsutsui and Mino) is considered [50]

Applications in Wireless Networks Packet Routing l Using optimal control approach, feedback Nash equilibrium strategies of this game can be expressed as follows l Iterative approach based on greedy adjustment is proposed to obtain the solution l Algorithm gradually increases the forwarding rate of the player as long as the payoff is non-decreasing l If the payoff of one player decreases, the algorithm will allow the other players to adjust the forwarding rate until none of players can gain a higher payoff [51]

Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l In heterogeneous wireless network, user can access multiple wireless networks (e. g. , 3 G, Wi. Fi, Wi. MAX) l However, none of the existing works consider the dynamic bandwidth allocation in heterogeneous wireless networks in which the users can change service selection dynamically l The network systems are naturally dynamic, a steady state of the network may never be reached l Therefore, the dynamic optimal control is the suitable approach for analyzing the dynamic decision making process Z. Kun, D. Niyato, and P. Wang, "Optimal bandwidth allocation with dynamic service selection in heterogeneous wireless networks, " in Proceedings of IEEE GLOBECOM'10, Miami FL USA, 6 -10 December 2010. [52]

Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l Designing a dynamic game framework for optimal bandwidth allocation under dynamic service selection – For service providers: the profit can be maximized – For users: the performance can be maximized under competition [53]

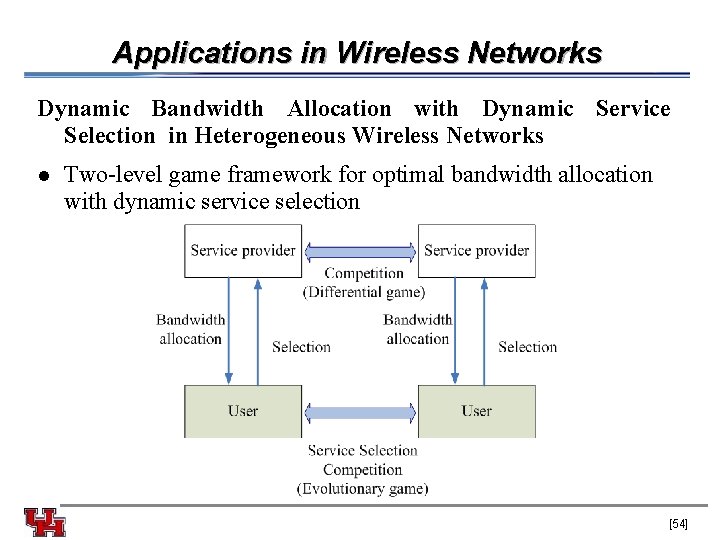
Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l Two-level game framework for optimal bandwidth allocation with dynamic service selection [54]

Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l Game formulation: Evolution of Service Selection – Players: N active users in area a – Strategy: The choices of particular service class from certain service providers – Payoff: The payoff of user k selecting service class j from service provider i : – The replicator dynamics modeling the service selection: [55]

Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l Game formulation: Dynamic Bandwidth Allocation – Players: M service providers in area a – Control strategies: The control strategy of player i denoted by – Open-loop vs Closed-loop – System state: – The instantaneous payoff: [56]

Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l Optimal Control Formulation [57]

Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l Open-loop Nash equilibrium [58]

Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l Pontryagin’s Maximum Principle for Nash Equilibrium A strategy profile is Nash Equilibrium if there exists for every optimal control path such that the following conditions are satisfied – The maximum condition holds for all players – Adjoint equation holds for all i, j – The constraints and boundary conditions are satisfied – is concave and continuously differentiable [59]

Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l Cooperative Bandwidth Allocation – Maximize: – The Hamiltonian function: – Observation: In the non-cooperative bandwidth allocation differential game, the selfish behavior of service providers can also maximize the social welfare [60]

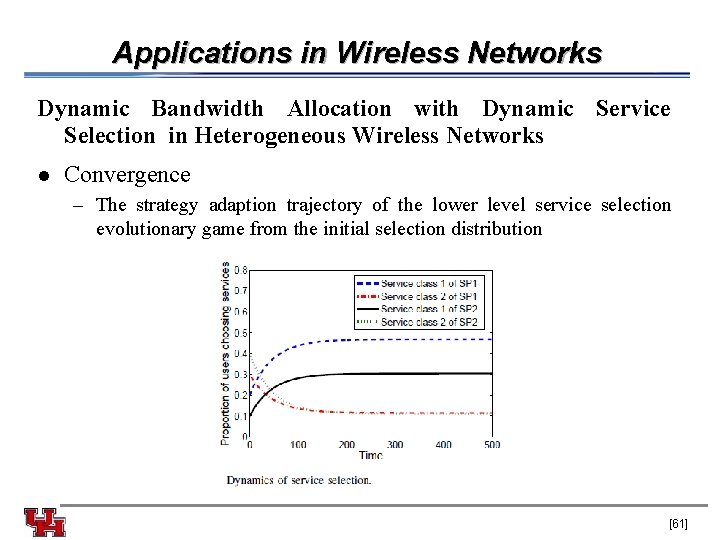
Applications in Wireless Networks Dynamic Bandwidth Allocation with Dynamic Service Selection in Heterogeneous Wireless Networks l Convergence – The strategy adaption trajectory of the lower level service selection evolutionary game from the initial selection distribution [61]

Summary l The basics of differential game have been discussed l Two applications of differential game in wireless network, i. e. , routing and bandwidth allocation have been presented l Differential game can be used in other applications (e. g. , cognitive radio) which are open to exploration [62]