Game Theory Fred Wenstp Zero sum games Introduction

Game Theory Fred Wenstøp

Zero sum games Introduction – Games where one player wins what the other player loses • Co-operation is out of question • Conventions: – Players: Row and Column • Row chooses a row • Column chooses a column • Choices are made independently and simultaneously – The table shows Row's result • Row wants big numbers • Column wants small numbers – The payoff table is known to both players 12/7/2020 Fred Wenstøp 2

Zero sum games Analysis of dominance • Column thinks that Row thinks this – Therefore Row will choose R 2 since it is dominating • Row thinks: – Column will never choose C 1 because it is dominated – Therefore it boils down to: 12/7/2020 • The “solution” is R 2, C 2 Fred Wenstøp 3

Zero sum games Maximising security levels • If there is no dominance: – Find the row that maximises Rows security level (R 2) – Find the column that minimises Columns security level (C 1) – Saddle point: minimax = maximin – a stable solution since no player can gain by a unilateral move – It is called a Nash equilibrium • But not all games have saddle points. . . 12/7/2020 Fred Wenstøp 4

Zero sum games Mixed strategies • In this case R 2 maximises Rows security level C 2 minimises Columns security level • But, – minimax is not equal to maximin • Therefore Row chooses R 2 Column had planned to choose C 2 – but thinking that Row will choose R 2, he chooses C 1 instead Row thinks that column thinks this – Therefore, Row chooses R 1 Column thinks that Row thinks this. . 12/7/2020 The solution? Do something unexpected! The game of pure strategies Fred Wenstøp 5

Zero sum games Mixed strategies • Row introduces a new strategy which is a mix of R 1 and R 2 – Rmixed: • Choose R 1 with probability 4/11 • This increases the security level from 3 to 5. 2 • Column introduces a new strategy which is a mix of C 1 and C 2 – Rmixed: • Choose C 1 with probability 5/11 • This improves the security level from 7 to 5. 2 • We have created a new Nash equilibrium! 12/7/2020 Fred Wenstøp 6

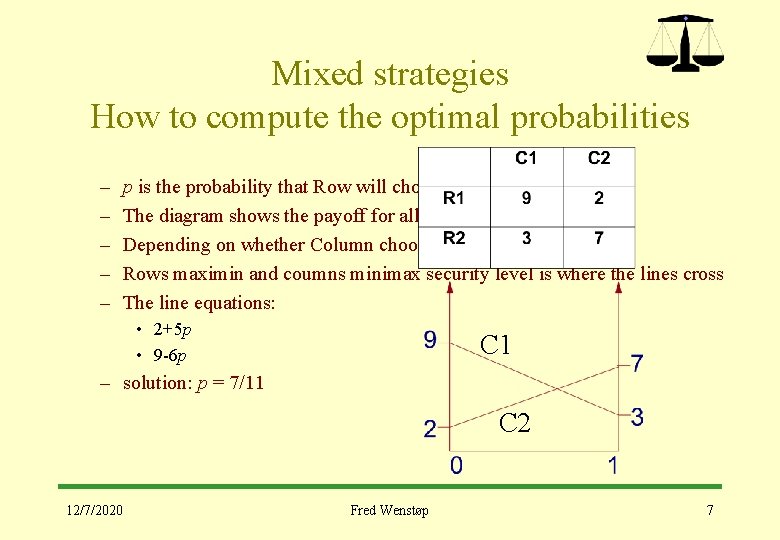
Mixed strategies How to compute the optimal probabilities – – – p is the probability that Row will choose R 2 The diagram shows the payoff for all values off p Depending on whether Column chooses C 1 or C 2 Rows maximin and coumns minimax security level is where the lines cross The line equations: • 2+5 p • 9 -6 p C 1 – solution: p = 7/11 C 2 12/7/2020 Fred Wenstøp 7

Games with possibilities for co-operation • The size of the pie depends on both players' moves – This invites to co-operation • Conventions – Both players' result is shown in the table, Row's result first • Several classes of games – Little or now conflict – Games with possibilities for threats – Games with possibilities for coercion – Battle of the sexes games – Prisoners' dilemma games 12/7/2020 Fred Wenstøp 8

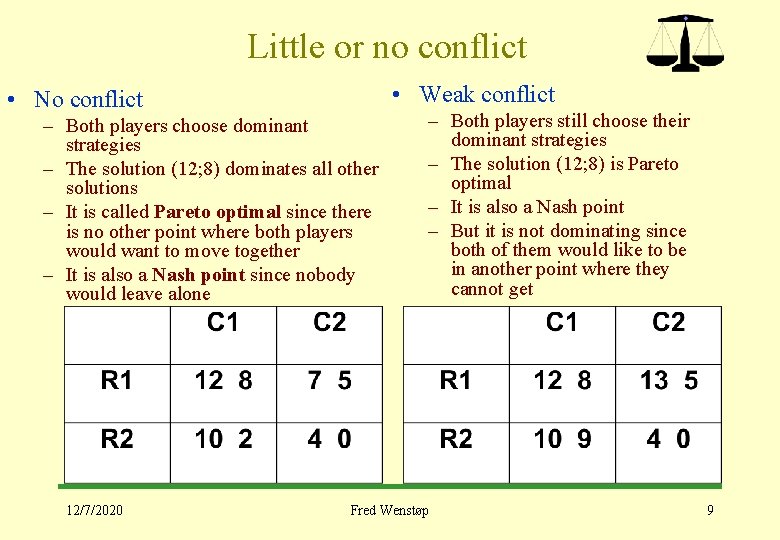
Little or no conflict • Weak conflict • No conflict – Both players choose dominant strategies – The solution (12; 8) dominates all other solutions – It is called Pareto optimal since there is no other point where both players would want to move together – It is also a Nash point since nobody would leave alone 12/7/2020 – Both players still choose their dominant strategies – The solution (12; 8) is Pareto optimal – It is also a Nash point – But it is not dominating since both of them would like to be in another point where they cannot get Fred Wenstøp 9

Games with possibilities for threats • The Seller sets the price • The buyer decides on the quantity – If both players choose their dominant strategies, the solution will be – Q=much, P=high • Pareto-optimal • Nash-point • Non-dominating • Buyer can threaten to buy little if Seller does not lower the price – In this case, Seller is vulnerable – New solution: Q=much, P=low • Pareto-optimal • Not a Nash-point • Non-dominating 12/7/2020 Fred Wenstøp 10

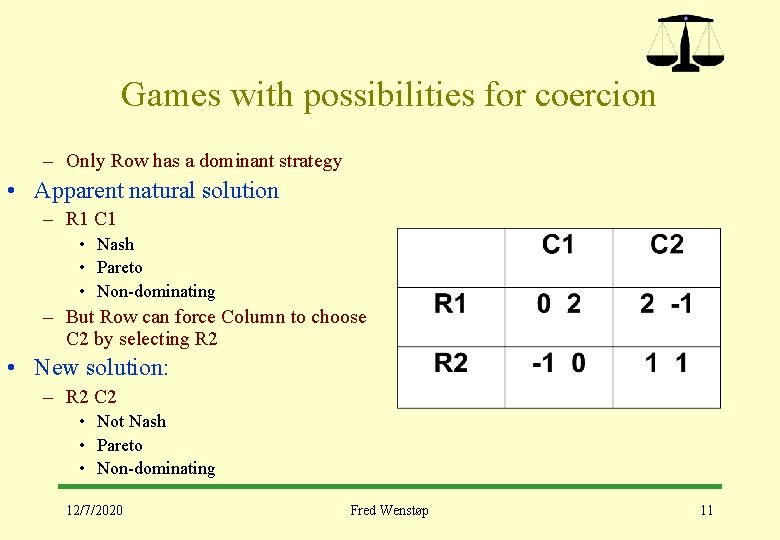
Games with possibilities for coercion – Only Row has a dominant strategy • Apparent natural solution – R 1 C 1 • Nash • Pareto • Non-dominating – But Row can force Column to choose C 2 by selecting R 2 • New solution: – R 2 C 2 • Not Nash • Pareto • Non-dominating 12/7/2020 Fred Wenstøp 11

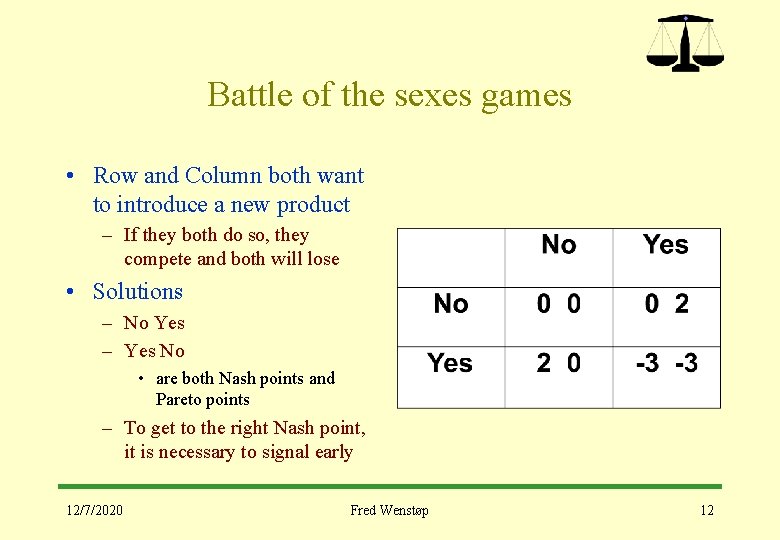
Battle of the sexes games • Row and Column both want to introduce a new product – If they both do so, they compete and both will lose • Solutions – No Yes – Yes No • are both Nash points and Pareto points – To get to the right Nash point, it is necessary to signal early 12/7/2020 Fred Wenstøp 12

The prisoners' dilemma • Two persons are accused of a serious crime • Dominant strategies: – They cannot be convicted unless at least one confesses and turn state evidence against the other – If both do this, they will each get 8 years – If only one confesses, the other will get 10 years – If none confesses, both will be convicted of a minor offence and get 2 years 12/7/2020 Fred Wenstøp – Confess – Solution: 8 8 • Nash point • Not at all Pareto Optimal • Dominated 13