GAME THEORY AND APPLICATIONS DOMINANT STRATEGY Assoc Prof

GAME THEORY AND APPLICATIONS DOMINANT STRATEGY Assoc. Prof. Yeşim Kuştepeli 1

Static Game with Pure strategies • Dominant strategy: Strategy S 1 strictly dominates S 2 for a player if given any collection of strategies that could be played by the other players, playing S 1 results in a strictly higher payoff for that player than playing S 2. • S 2 is said to be strictly dominated by S 1. • The strategy profile {S 1, S 2, …. } is a strictly dominant strategy equilibrium if for every player i, Si is a strictly dominant strategy. Assoc. Prof. Yeşim Kuştepeli 2

• Weakly Dominant strategy: Strategy S 1 weakly dominates S 2 for a player if given any collection of strategies that could be played by the other players, playing S 1 never results in a lower payoff for that player than playing S 2 and in at least one instance S 1 gives the player a strictly higher payoff than does S 2. • S 2 is said to be weakly dominated by S 1. • The strategy profile {S 1, S 2, …. } is a weakly dominant strategy equilibrium if for every player i, Si is a weakly dominant strategy. Assoc. Prof. Yeşim Kuştepeli 3

• Iterated Dominant strategy: Strategy S 1 is an iterated strictly dominant strategy for a player if and only if it is the only strategy in the intersection of the following sequence of rested sets of strategies: • 1) Si, 1 consists of all of player i’s strategies that are not strictly dominated • 2) for n>1 Si, n consists of strategies in Si, n-1 that are not strictly dominated when we restrict the other players to the strategies in Sj, n-1. • The strategy profile {S 1, S 2, …. Sn} is an iterated strictly dominant strategy equilibrium if for every player i, Si is a iterated strictly dominant strategy. Assoc. Prof. Yeşim Kuştepeli 4

• A Nash equilibrium is a strategy profile {S 1*, S 2*, …. Sn*} such that each strategy Si* is an element of set of possible strategies and maximixes the function fi(x)= vi(Si*, …. . Si-1*, x, Si+1*, …. . Sn*) among the elements of the possible strategy set. • At a Nash equilibirum , each player’s equilibrium strategy is a best-response to the belief that the other players will adopt their Nash equilibirum strategies. Assoc. Prof. Yeşim Kuştepeli 5

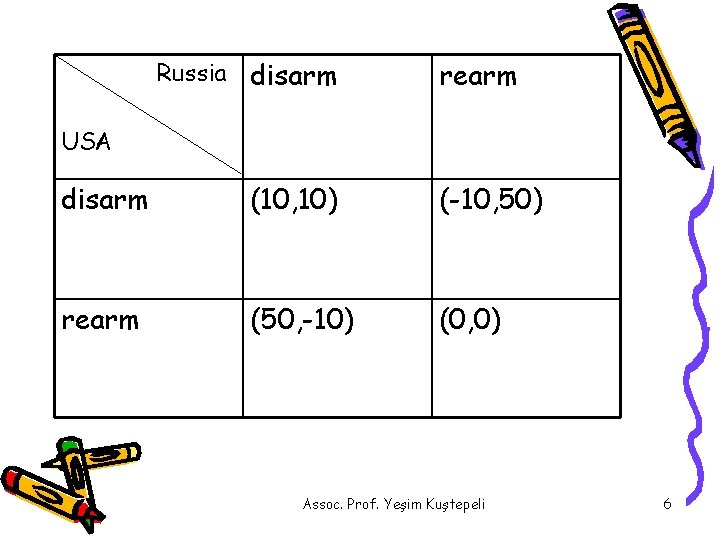
Russia disarm rearm USA disarm (10, 10) (-10, 50) rearm (50, -10) (0, 0) Assoc. Prof. Yeşim Kuştepeli 6

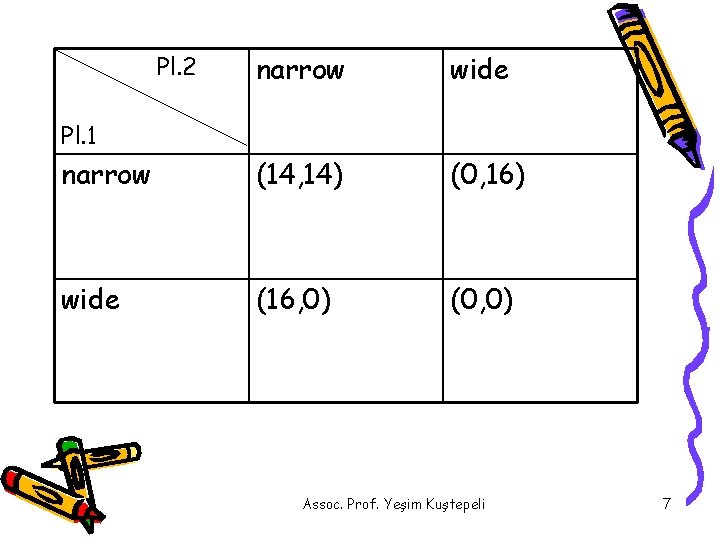
narrow wide narrow (14, 14) (0, 16) wide (16, 0) (0, 0) Pl. 2 Pl. 1 Assoc. Prof. Yeşim Kuştepeli 7

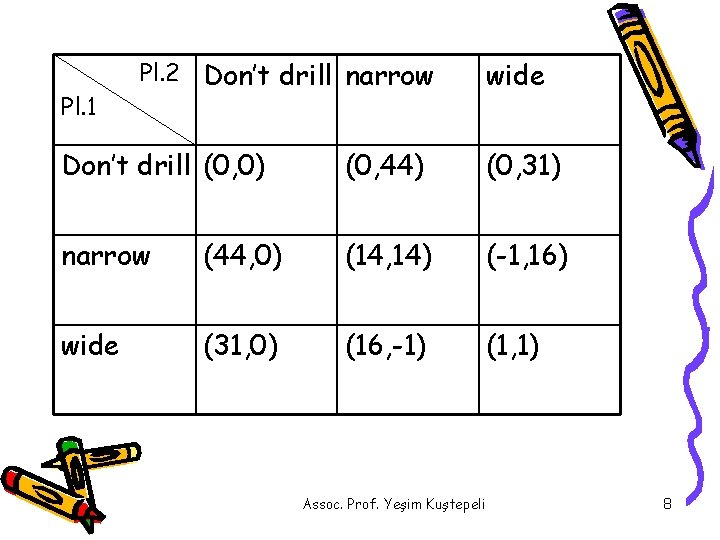
Pl. 1 Pl. 2 Don’t drill narrow wide Don’t drill (0, 0) (0, 44) (0, 31) narrow (44, 0) (14, 14) (-1, 16) wide (31, 0) (16, -1) (1, 1) Assoc. Prof. Yeşim Kuştepeli 8