GAME THEORY AND APPLICATIONS Definition of Games Types

GAME THEORY AND APPLICATIONS

• Definition of Games, Types, Components • Representation of Game • Finding Game Equilibrium – Dominant Strategy – Nash Equilibrium and Problems – Repeated Games – Sequential Game • Applications

Definition • Game : Any situation in which players make strategy decision, decision that take into account each other’ s action and responses. • Components ( ����� ) – Players ( ������� ) – Rules of Game ( �� ����� ) ��� Strategy ( ������� ) – Payoff ( ������� )

• Payoff : Outcome of game that generates reward or benefit for the player. • Strategy : Rule or plan of action for playing a game • Optimal Strategy : Strategy that maximizes player’ s expected payoff.

Types of Games • • Simultaneous VS Sequential Game Cooperative VS Non - Cooperative Game One - Shot Game VS Repeated Game Constant sum VS Non - Constant sum Game

Representation 1. Normal Form : B ��� A ��� 2 , -2 ���� 2 , 2 - ���� 2 , 22 - , 2

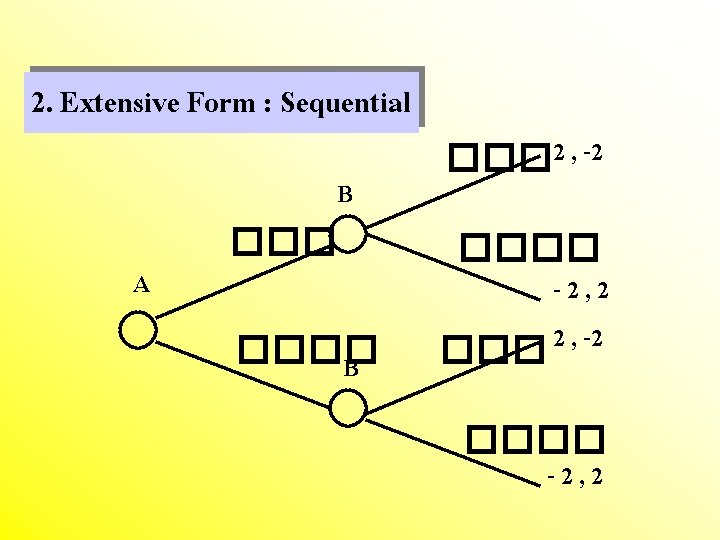
2. Extensive Form : Sequential B A ���� B ��� 2 , -2 ���� -2, 2

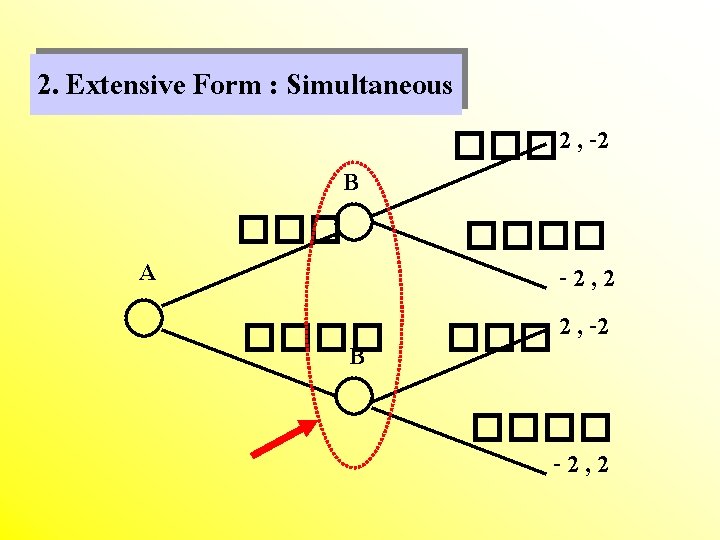
2. Extensive Form : Simultaneous B A ���� B ��� 2 , -2 ���� -2, 2

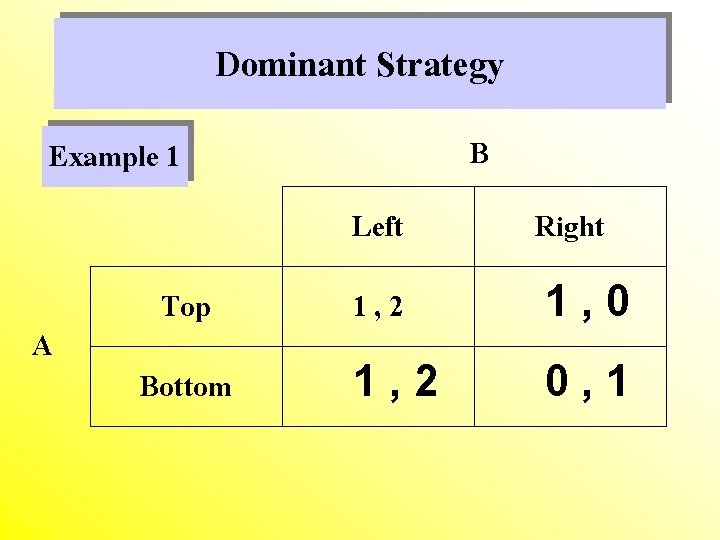
Dominant Strategy B Example 1 A Top Bottom Left Right 1, 2 1, 0 1, 2 0, 1

Example 2 B Advertise A Advertise Don ’ t Don ‘ t 10 , 5 0 , 15 8, 6 2 , 10

Nash Equilibrium VS Dominant Strategy Example 3 A Advertise Don ’ t B Advertise Don ‘ t 10 , 5 0 , 15 8, 6 2 , 10

Example 4 B Advertise A Advertise Don ’ t Don ‘ t 10 , 5 0 , 15 8, 6 2 , 20

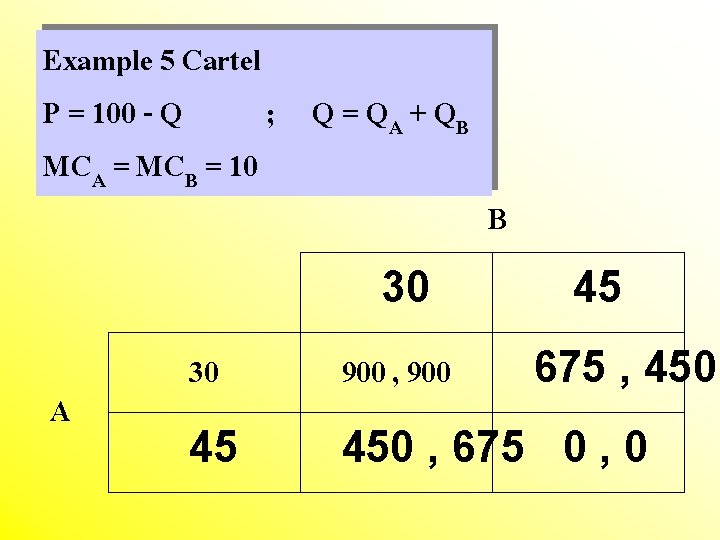
Example 5 Cartel P = 100 - Q ; Q = Q A + QB MCA = MCB = 10 30 A B 45 30 900 , 900 45 450 , 675 0 , 0 675 , 450

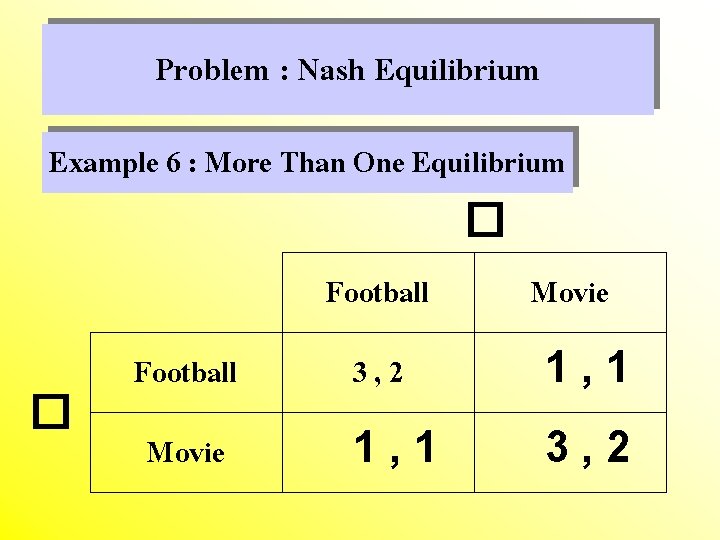
Problem : Nash Equilibrium Example 6 : More Than One Equilibrium � Football � Movie Football 3, 2 1, 1 Movie 1, 1 3, 2

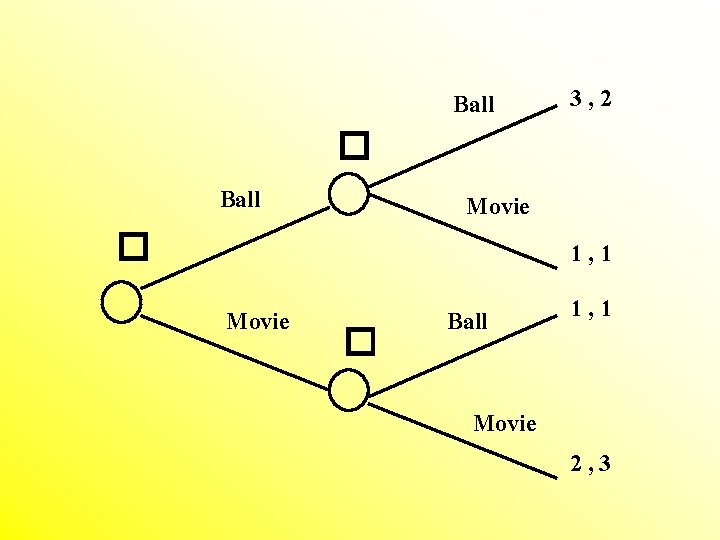
� Ball Movie � Movie Ball � Ball Movie 3, 2 1, 1 2, 3

Problem : Nash Equilibrium Example 7 : No Equilibrium � ������ 0, 0 ������ 1 , 0 0 , 1 � ���� 0 , 1 0 , 0 1, 0 ������ 0 , 1 0 , 0

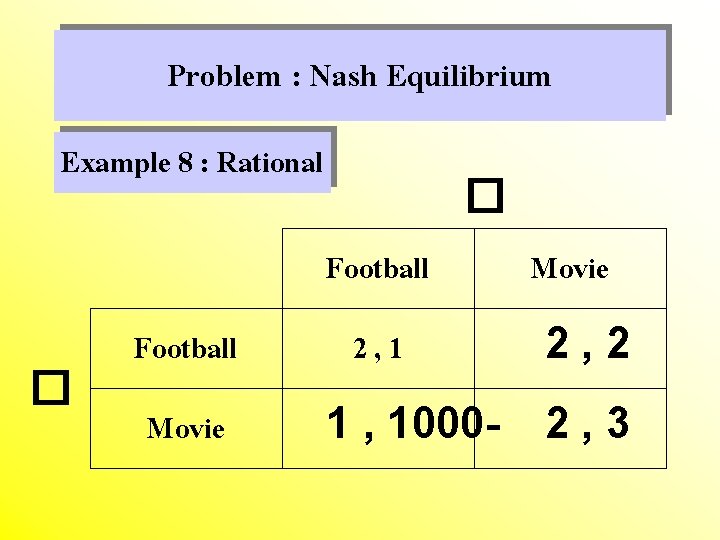
Problem : Nash Equilibrium Example 8 : Rational � Football Movie 2, 1 1 , 1000 - Movie 2, 2 2, 3

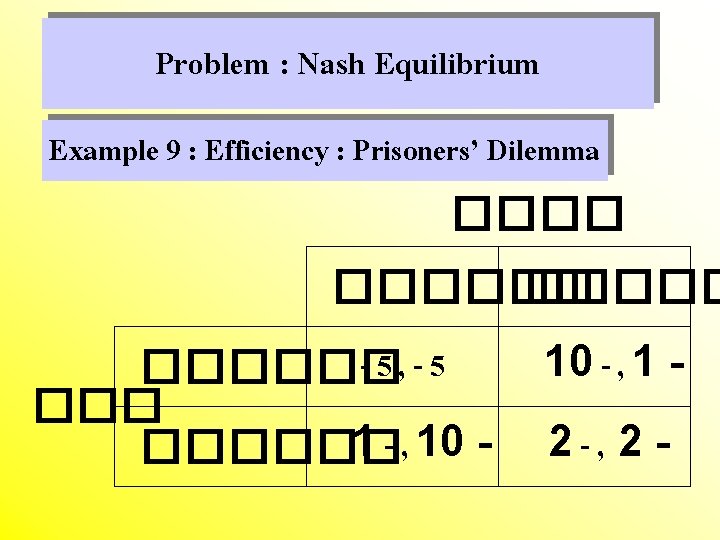
Problem : Nash Equilibrium Example 9 : Efficiency : Prisoners’ Dilemma ������ -5, -5 ������ 1 - , 10 ������ 10 - , 1 2 -, 2 -

Example 10 : Prisoners’ Dilemma and Cartel B A More Quota More 2, 2 1 , 4 Quota 4, 1 3 , 3

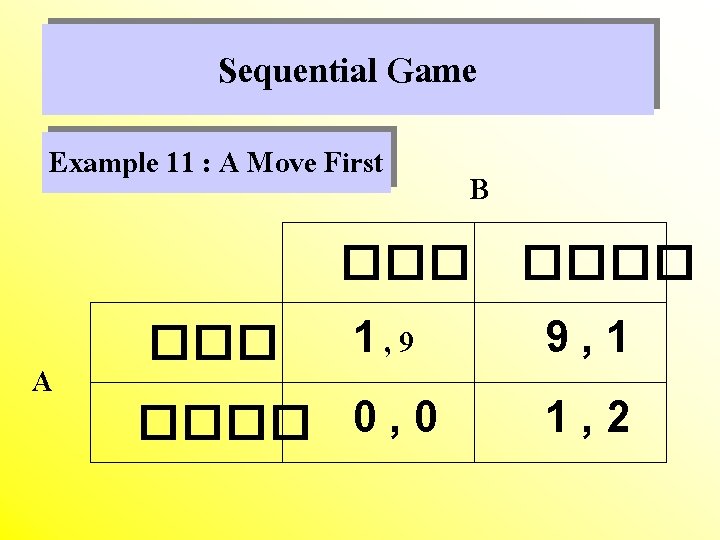
Sequential Game Example 11 : A Move First B ��� A ��� 1, 9 ���� 0 , 0 ���� 9, 1 1, 2

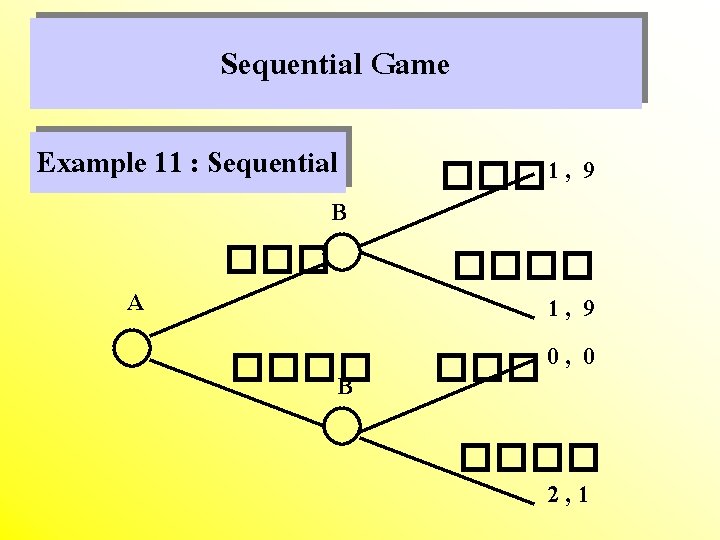
Sequential Game Example 11 : Sequential ��� 1 , 9 ���� 1, 9 0 , 0 ��� B A ���� B ���� 2, 1

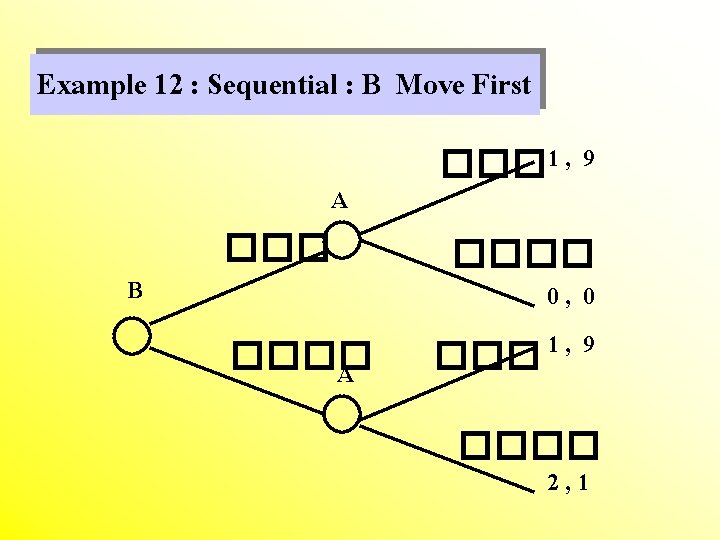
Example 12 : Sequential : B Move First A B ���� A ��� 1 , 9 ���� 0, 0 1 , 9 ���� 2, 1

Entry Deterrence Example 13 : A Move First B ������� A 0 , 10 ���� 5, 0 5, 2 ������� 4, 2 -

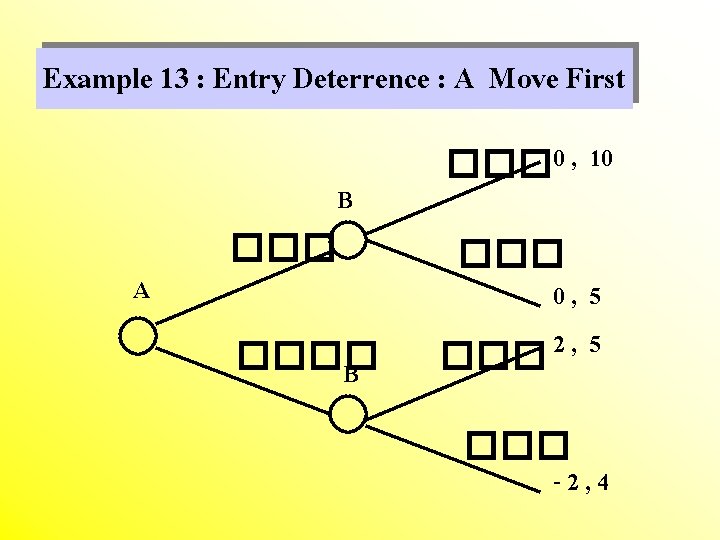
Example 13 : Entry Deterrence : A Move First B A ���� B ��� 0 , 10 ��� 0, 5 2 , 5 ��� -2, 4

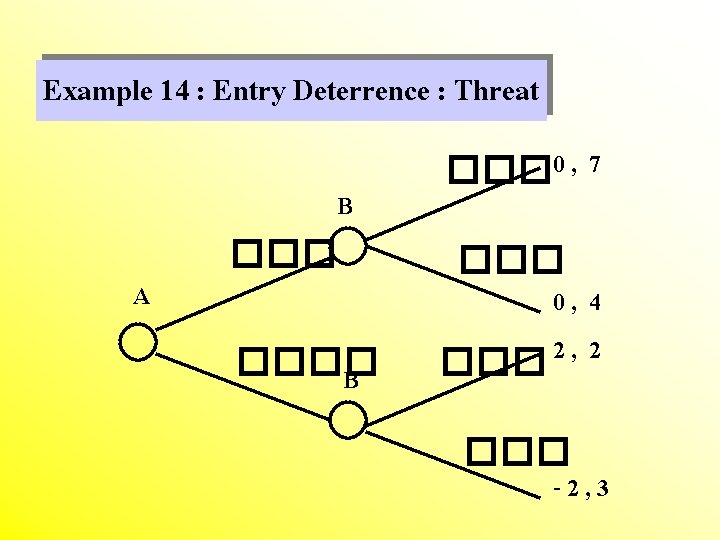
Example 14 : Entry Deterrence : Threat B A ���� B ��� 0 , 7 ��� 0, 4 2 , 2 ��� -2, 3

Problem : Nash Equilibrium Example 15 : Apply Problem: P = 30 - Q, MC = 0 Firm B 7. 5 Firm A 10 15 7. 5 112. 5, 112. 5125 , 93. 75 112. 5 , 56. 10 93. 75 , 125 100 , 10075 , 50 15 56. 25 , 112. 5 50 , 75 0 , 0