Galerkins Method for Differential Equation I In order











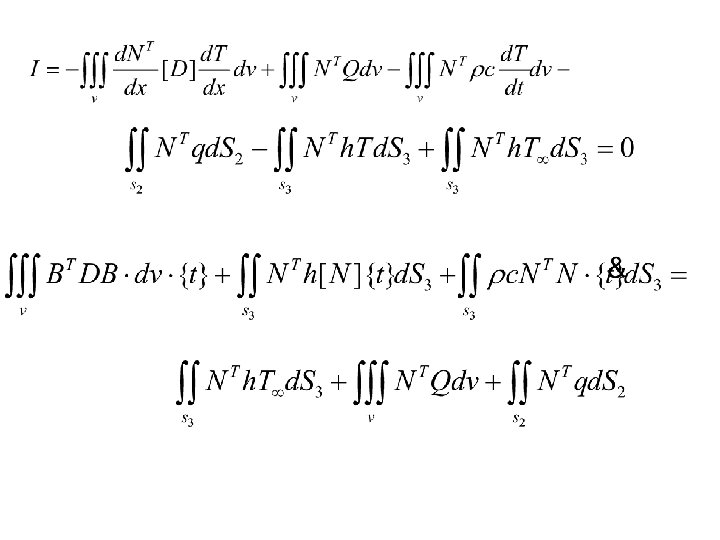



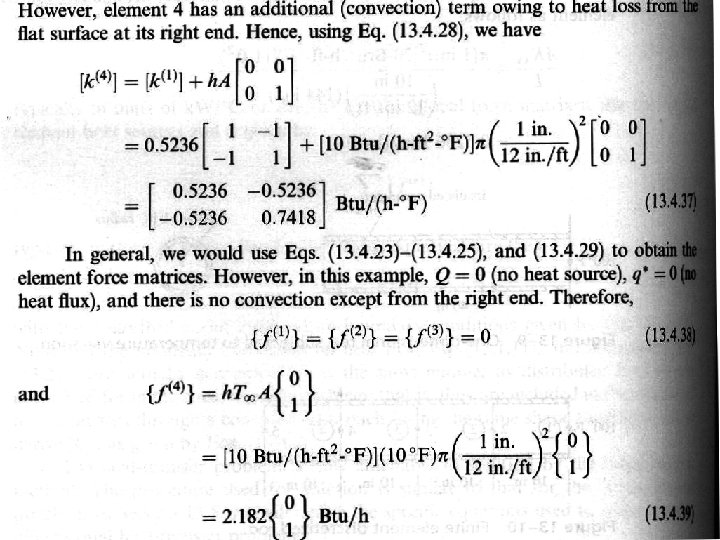





![Finite Element 2 -D Conduction Define Temperature Gradient Relationships Analogous to strain matrix: {g}=[B]{t} Finite Element 2 -D Conduction Define Temperature Gradient Relationships Analogous to strain matrix: {g}=[B]{t}](https://slidetodoc.com/presentation_image_h2/1ea9a5300ba62e0a380a9b8306909f1d/image-26.jpg)


- Slides: 28

Galerkin’s Method for Differential Equation (I) In order to make the residue a minimum at least at few selected nodal points, we use orthogonality condition

(II) Integrating the first term of equation II Equation II becomes

The first term is based on initial boundary conditions. For the given problem dy/dx is known only at x = o, and at subsequent points at x = l, 2 L …. is not known and hence subsequent terms are ignored.

Using the conditions dy/dx = y 1 = 0 and solving the system of equations, y 2, y 3, and y 4 can be solved

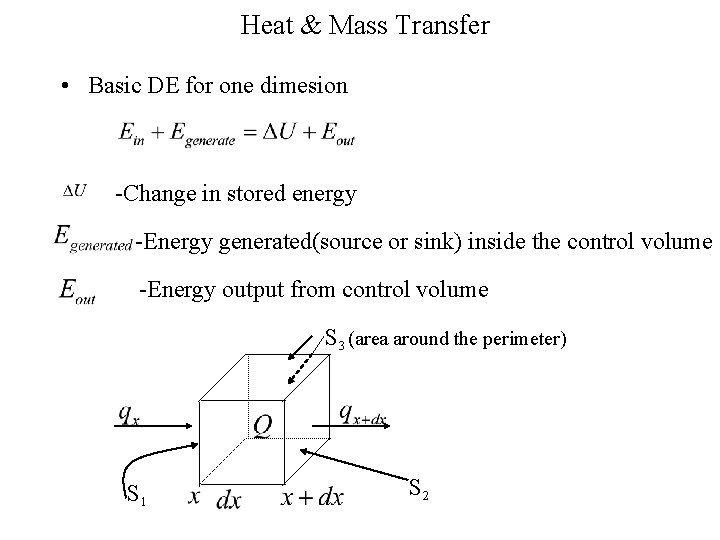
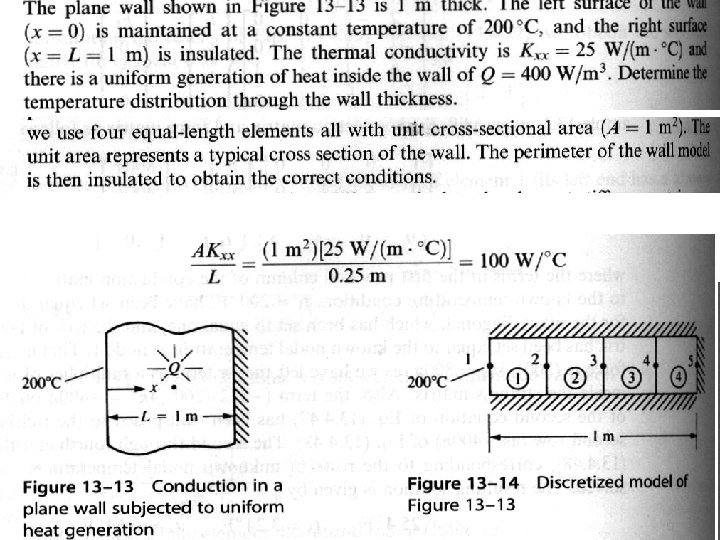
Heat & Mass Transfer

Heat & Mass Transfer • Basic DE for one dimesion -Change in stored energy -Energy generated(source or sink) inside the control volume -Energy output from control volume S 3 (area around the perimeter) S 1 S 2

- heat conducted(heat influx) into the control volume at surface edge x (k. W/m 2 or Btu/h-ft 2) - heat conducted out of control volume at surface edge x+dx -the internal heat source(heat generated/unit volume) or a sink (heat drawn out of volume) (k. W/m 3 or Btu/h-ft 3) -Area of control volume surface From Fourier’s law of heat conduction -thermal conductivity in x direction -temperature; - Temperature gradient

Using Taylor expansion: The change in stored energy: -specific heat in k. Wh/kg

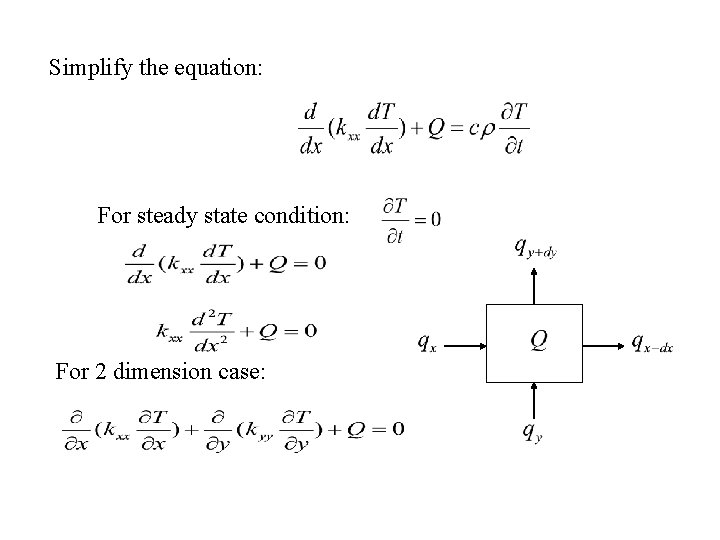
Simplify the equation: For steady state condition: For 2 dimension case:

Boundary Conditions

Heat transfer with conduction For a conducting solid in contact with fluid, there will be a heat transfer between solid and fluid. Heat flow by convection: -Heat transfer or convection coeffient -Temperature of solid surface -Temperature of liquid

One dimensional Problem 1 2 The temperature gradient matrix The heat flux/temperature gradient relationship is given by

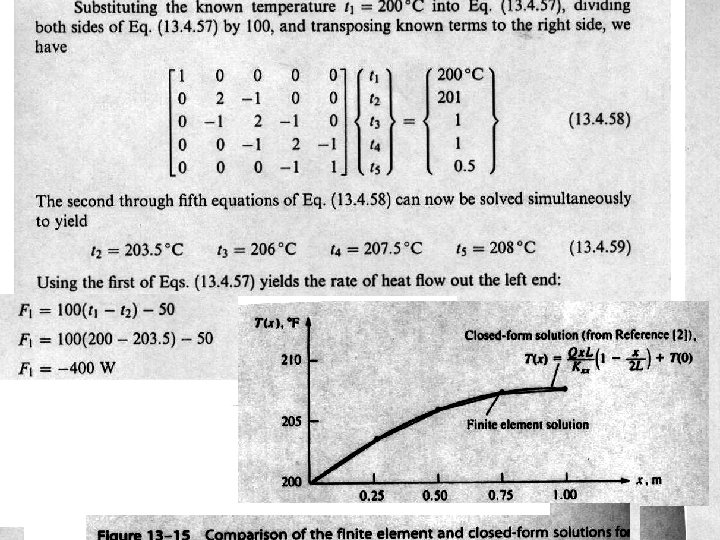
Casting the governing DE into integral form using Galcerkin approach. The last integrand can be written as
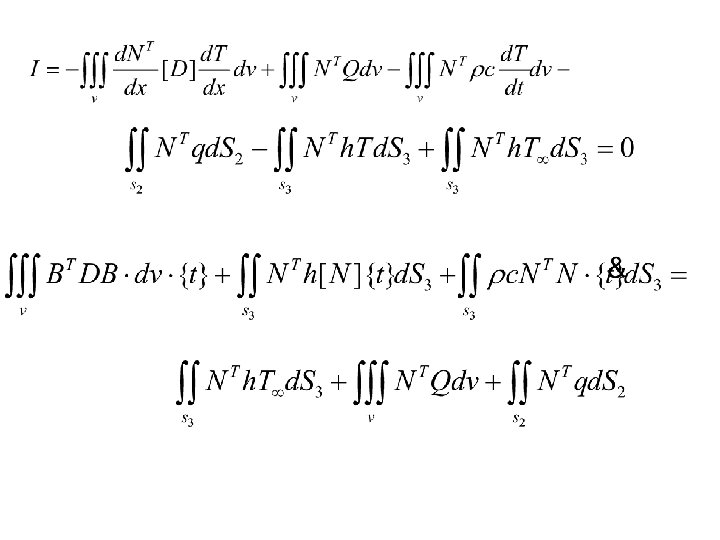

In case the surface S 2 convects heat in addition to heat flux, additional boundary Condition is required for the last element For the last element


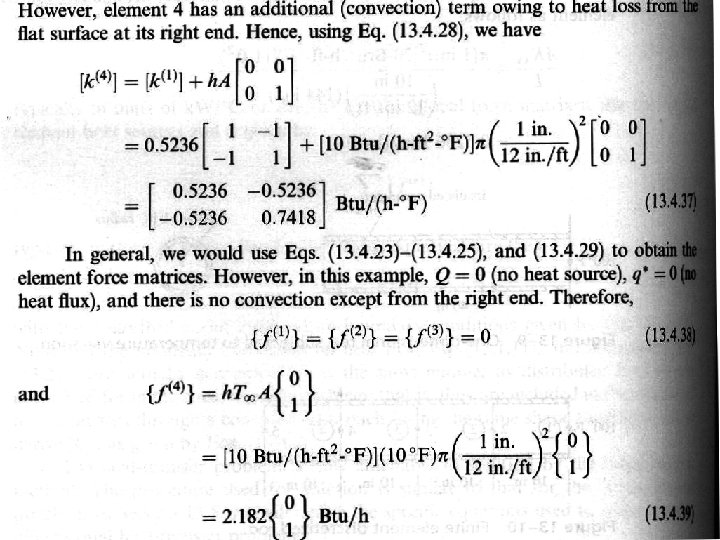





Structural vs Heat Transfer Structural Analysis Thermal Analysis • Select element type • Assume displacement function • Stress/strain relationships • Derive element stiffness • Assemble element equations • Solve nodal displacements • Solve element forces • Select element type • Assume temperature function • Temperature relationships • Derive element conduction • Assemble element equations • Solve nodal temperatures • Solve element gradient/flux

Finite Element 2 -D Conduction Assume (Choose) a Temperature Function Assume a linear temperature function for each element as: where u and v describe temperature gradients at (xi, yi). 3 Nodes 1 Element 2 DOF: x, y

Finite Element 2 -D Conduction Assume (Choose) a Temperature Function
![Finite Element 2 D Conduction Define Temperature Gradient Relationships Analogous to strain matrix gBt Finite Element 2 -D Conduction Define Temperature Gradient Relationships Analogous to strain matrix: {g}=[B]{t}](https://slidetodoc.com/presentation_image_h2/1ea9a5300ba62e0a380a9b8306909f1d/image-26.jpg)
Finite Element 2 -D Conduction Define Temperature Gradient Relationships Analogous to strain matrix: {g}=[B]{t} [B] is derivative of [N]

Finite Element 2 -D Conduction Derive Element Conduction Matrix and Equations i h j m

Stiffness matrix is general term for a matrix of known coefficients being multiplied by unknown degrees of freedom, i. e. , displacement OR temperature, etc. Thus, the element conduction matrix is often referred to as the stiffness matrix.