GABA Meeting Paris March 25 27 2009 Synchronization

GABA Meeting: Paris , March 25 -27, 2009 Synchronization Without Correlation Claudio R. Mirasso, M. Cornelles Soriano, G. Van der Sande, Ingo Fischer and Oscar Calvo Instituto de Física Interdisciplinar y Sistemas Complejos http: //ifisc. uib-csic. es – Palma de Mallorca - Spain

Synchronization without correlation Introduction Delayed coupled nonlinear oscillators can develop very interesting collective dynamical behavior. SCLs & Electronic circuits are ideal candidates for such studies: Ø Ø Ø They can be well controlled. Established models exist that can accurately describe their dynamics. Delays occur naturally when coupling them even for short separation distances. Synchronization between two or three mutually coupled SCL lasers have revealed unexpected properties. Two coupled SCL can achieve generalized synchronization at ± a delay time which coincides with the flying time of the light between the two lasers. ifisc. uib. es http: //ifisc. uib-csic. es – Palma de Mallorca - Spain

Synchronization without correlation Identical zero-lag synchronization is very difficult to observe in two bidirectionally coupled identical dynamical systems. A third mediating element easily allows for identical zero-lag synchronization of the outer SCLs placed in a chain (I. Fischer et al. Phys. Rev. Lett. 97, 123902, 2006) or between neuron populations (R. Vicente et al. , PNAS 109) “Dynamical relaying can yield zero time lag neuronal synchrony despite long conduction delays”, R. Vicente 105, 17157 (2008). . Identical synchronization between two dynamical systems obtained via a mediating elements is a general and robust property. ifisc. uib. es http: //ifisc. uib-csic. es – Palma de Mallorca - Spain

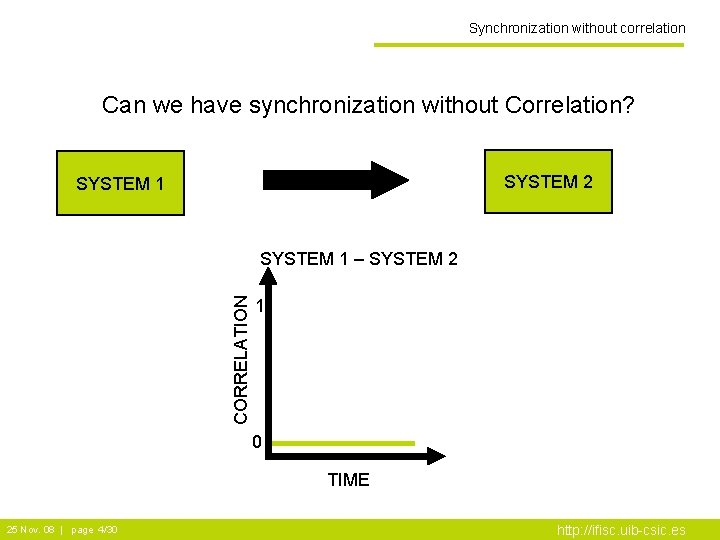
Synchronization without correlation Can we have synchronization without Correlation? SYSTEM 2 SYSTEM 1 CORRELATION SYSTEM 1 – SYSTEM 2 1 0 TIME 25 Nov. 08 | page 4/30 http: //ifisc. uib-csic. es

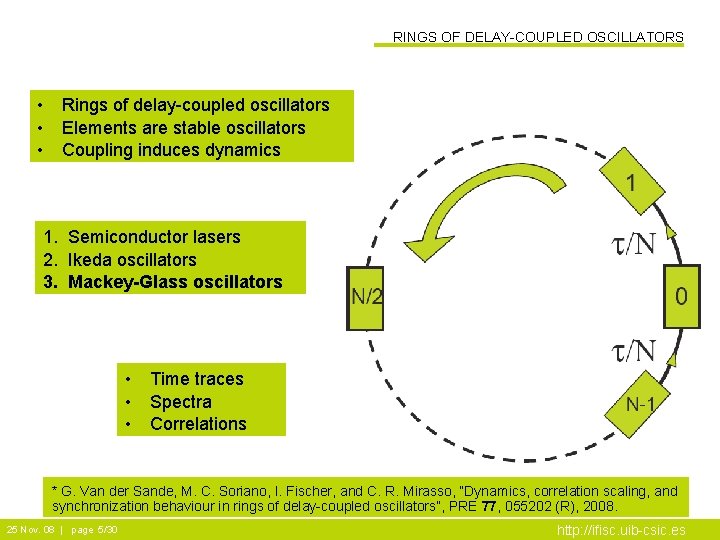
RINGS OF DELAY-COUPLED OSCILLATORS • • • Rings of delay-coupled oscillators Elements are stable oscillators Coupling induces dynamics 1. Semiconductor lasers 2. Ikeda oscillators 3. Mackey-Glass oscillators • • • Time traces Spectra Correlations * G. Van der Sande, M. C. Soriano, I. Fischer, and C. R. Mirasso, “Dynamics, correlation scaling, and synchronization behaviour in rings of delay-coupled oscillators”, PRE 77, 055202 (R), 2008. 25 Nov. 08 | page 5/30 http: //ifisc. uib-csic. es

OUTLINE • Ring dynamics • Ring correlation properties • Synchronization without correlation • Electronic analogue • Conclusions 25 Nov. 08 | page 6/30 http: //ifisc. uib-csic. es

MODEL • Coupled Mackey-Glass (MG) Oscillators: – Model of blood production D. Mackey and L. Glass, Science 197, 287 (1977) 25 Nov. 08 | page 7/30 http: //ifisc. uib-csic. es

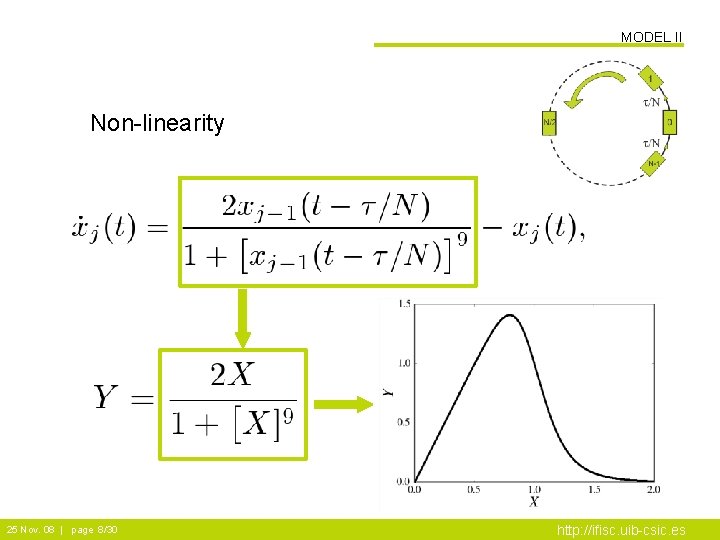
MODEL II Non-linearity 25 Nov. 08 | page 8/30 http: //ifisc. uib-csic. es

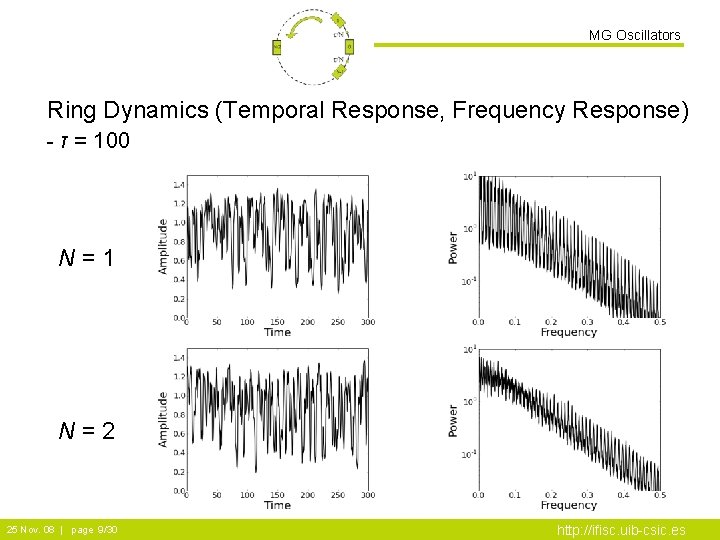
MG Oscillators Ring Dynamics (Temporal Response, Frequency Response) - τ = 100 N=1 N=2 25 Nov. 08 | page 9/30 http: //ifisc. uib-csic. es

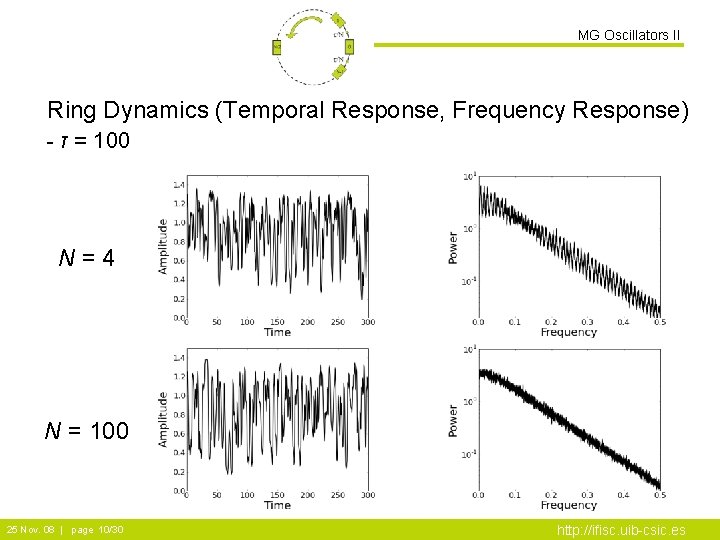
MG Oscillators II Ring Dynamics (Temporal Response, Frequency Response) - τ = 100 N=4 N = 100 25 Nov. 08 | page 10/30 http: //ifisc. uib-csic. es

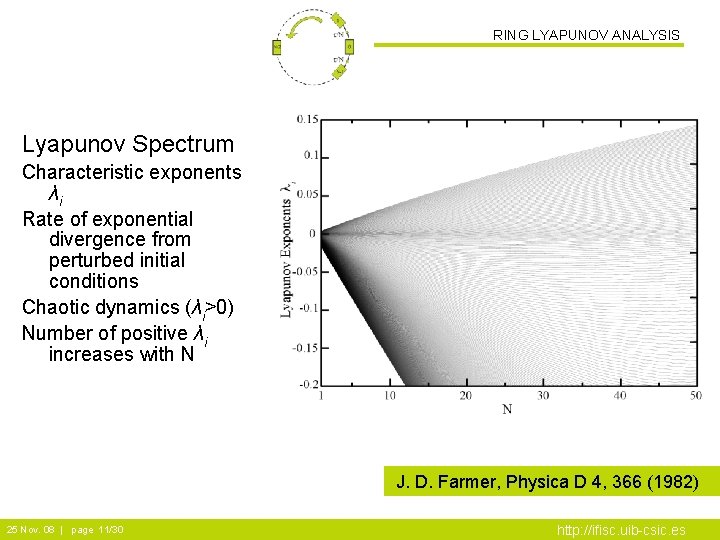
RING LYAPUNOV ANALYSIS Lyapunov Spectrum Characteristic exponents λi Rate of exponential divergence from perturbed initial conditions Chaotic dynamics (λi>0) Number of positive λi increases with N J. D. Farmer, Physica D 4, 366 (1982) 25 Nov. 08 | page 11/30 http: //ifisc. uib-csic. es

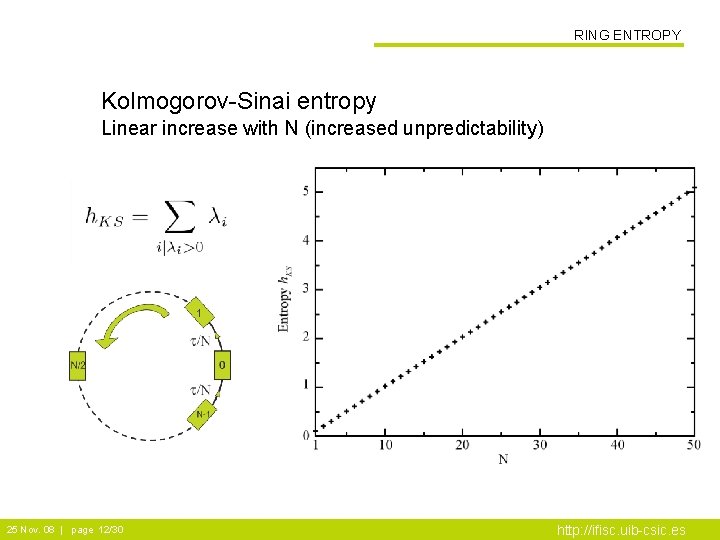
RING ENTROPY Kolmogorov-Sinai entropy Linear increase with N (increased unpredictability) 25 Nov. 08 | page 12/30 http: //ifisc. uib-csic. es

CORRELATION Quantifying the synchronization – Correlation between ring elements – Other non-linear methods, e. g. Mutual Information. . . 25 Nov. 08 | page 13/30 http: //ifisc. uib-csic. es

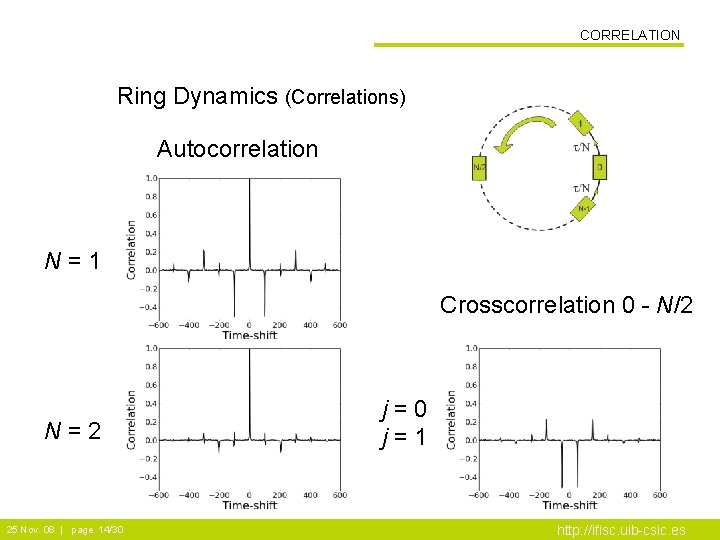
CORRELATION Ring Dynamics (Correlations) Autocorrelation N=1 Crosscorrelation 0 - N/2 N=2 25 Nov. 08 | page 14/30 j=1 http: //ifisc. uib-csic. es

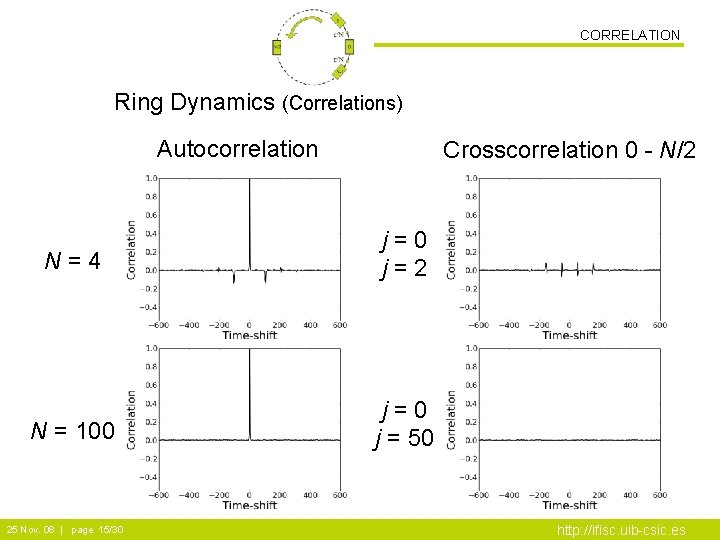
CORRELATION Ring Dynamics (Correlations) Autocorrelation Crosscorrelation 0 - N/2 N=4 j=0 j=2 N = 100 j=0 j = 50 25 Nov. 08 | page 15/30 http: //ifisc. uib-csic. es

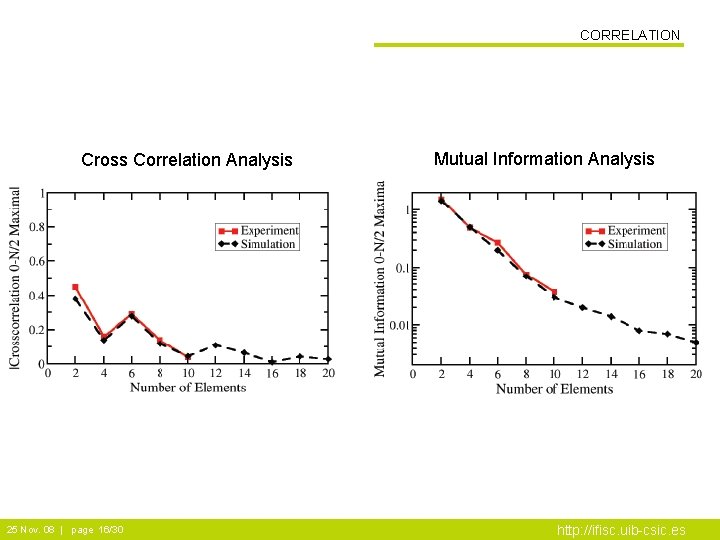
CORRELATION Cross Correlation Analysis 25 Nov. 08 | page 16/30 Mutual Information Analysis http: //ifisc. uib-csic. es

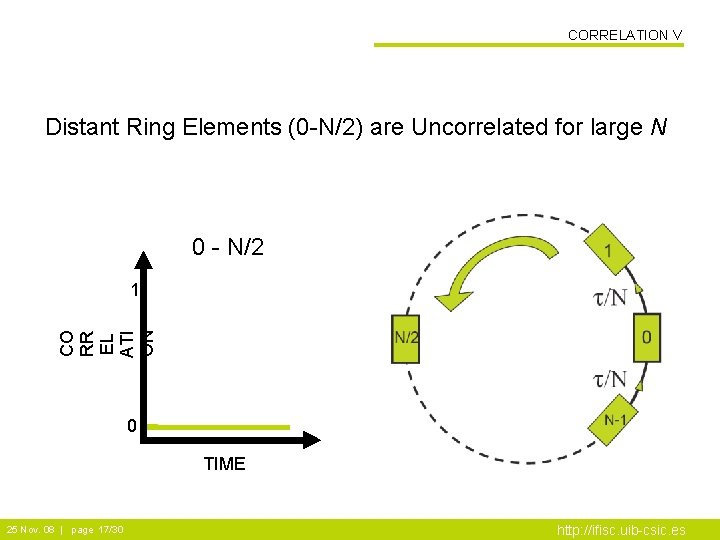
CORRELATION V Distant Ring Elements (0 -N/2) are Uncorrelated for large N 0 - N/2 CO RR EL ATI ON 1 0 TIME 25 Nov. 08 | page 17/30 http: //ifisc. uib-csic. es

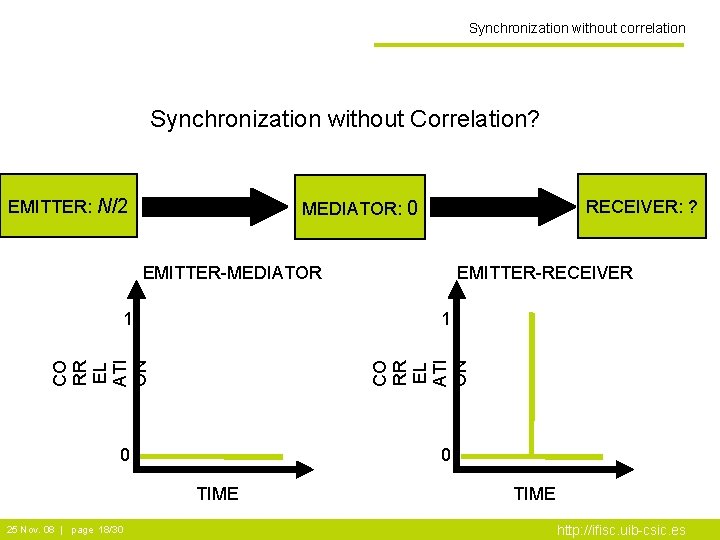
Synchronization without correlation Synchronization without Correlation? EMITTER: N/2 MEDIATOR: 0 RECEIVER: ? EMITTER-MEDIATOR CO RR EL ATI ON 1 0 0 TIME 25 Nov. 08 | page 18/30 EMITTER-RECEIVER TIME http: //ifisc. uib-csic. es

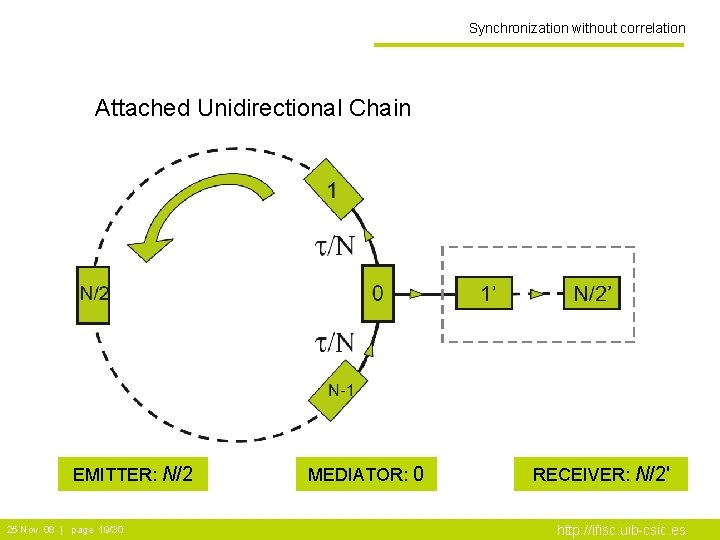
Synchronization without correlation Attached Unidirectional Chain EMITTER: N/2 25 Nov. 08 | page 19/30 MEDIATOR: 0 RECEIVER: N/2' http: //ifisc. uib-csic. es

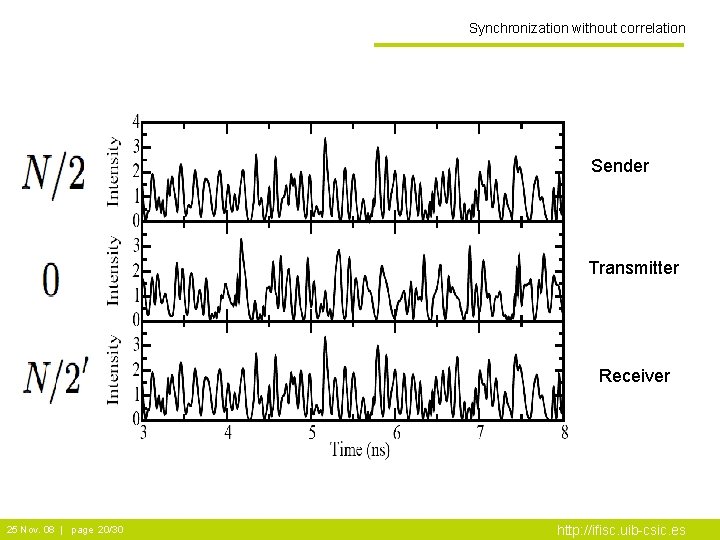
Synchronization without correlation Sender Transmitter Receiver 25 Nov. 08 | page 20/30 http: //ifisc. uib-csic. es

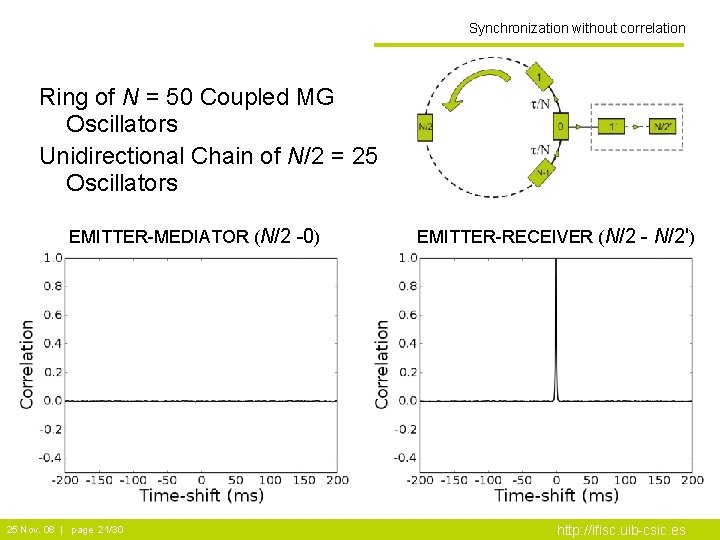
Synchronization without correlation Ring of N = 50 Coupled MG Oscillators Unidirectional Chain of N/2 = 25 Oscillators EMITTER-MEDIATOR (N/2 -0) 25 Nov. 08 | page 21/30 EMITTER-RECEIVER (N/2 - N/2') http: //ifisc. uib-csic. es

OUTLINE • Ring dynamics • Ring correlation properties • Synchronization without correlation • Electronic analogue • Conclusions 25 Nov. 08 | page 22/30 http: //ifisc. uib-csic. es

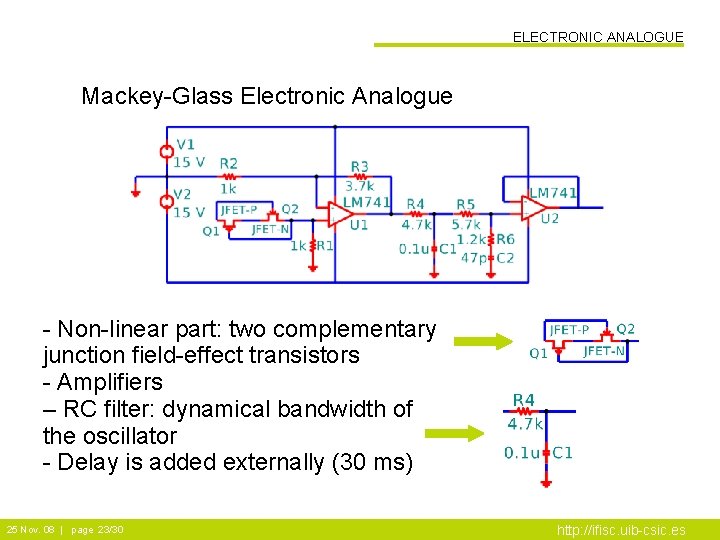
ELECTRONIC ANALOGUE Mackey-Glass Electronic Analogue - Non-linear part: two complementary junction field-effect transistors - Amplifiers – RC filter: dynamical bandwidth of the oscillator - Delay is added externally (30 ms) 25 Nov. 08 | page 23/30 http: //ifisc. uib-csic. es

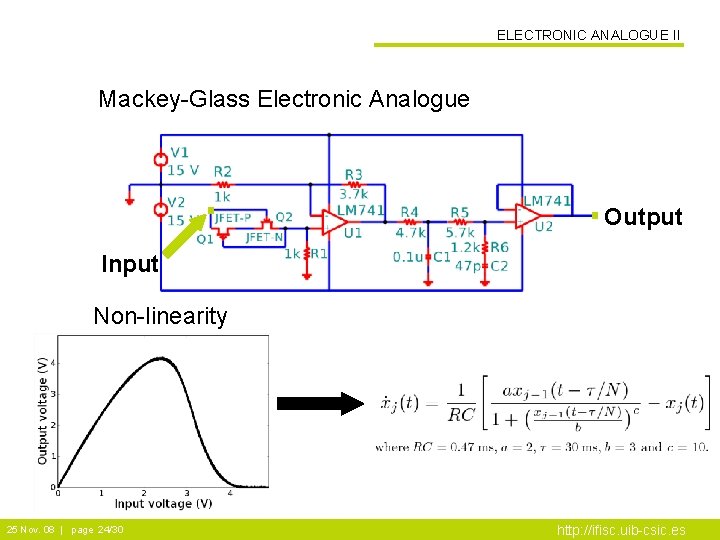
ELECTRONIC ANALOGUE II Mackey-Glass Electronic Analogue Output Input Non-linearity 25 Nov. 08 | page 24/30 http: //ifisc. uib-csic. es

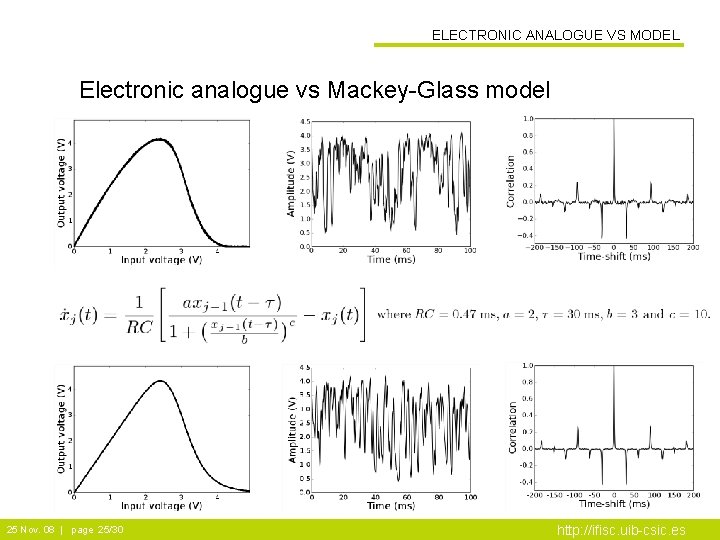
ELECTRONIC ANALOGUE VS MODEL Electronic analogue vs Mackey-Glass model 25 Nov. 08 | page 25/30 http: //ifisc. uib-csic. es

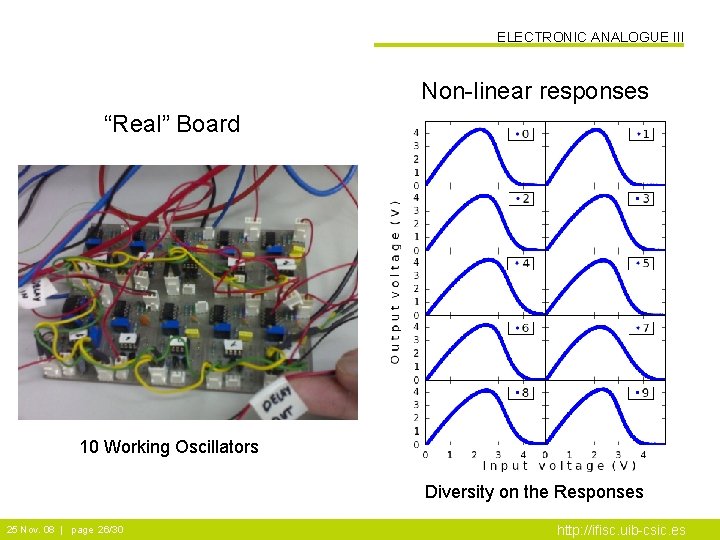
ELECTRONIC ANALOGUE III Non-linear responses “Real” Board 10 Working Oscillators Diversity on the Responses 25 Nov. 08 | page 26/30 http: //ifisc. uib-csic. es

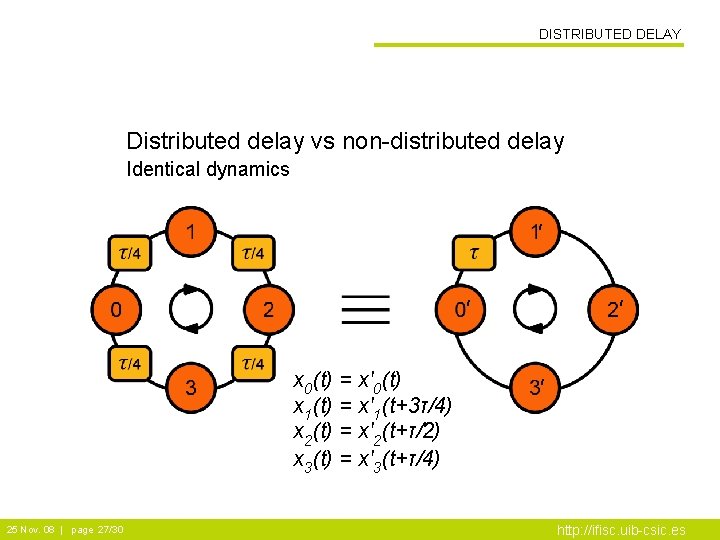
DISTRIBUTED DELAY Distributed delay vs non-distributed delay Identical dynamics ' ' x 0(t) = x'0(t) x 1(t) = x'1(t+3τ/4) x 2(t) = x'2(t+τ/2) x 3(t) = x'3(t+τ/4) 25 Nov. 08 | page 27/30 ' ' http: //ifisc. uib-csic. es

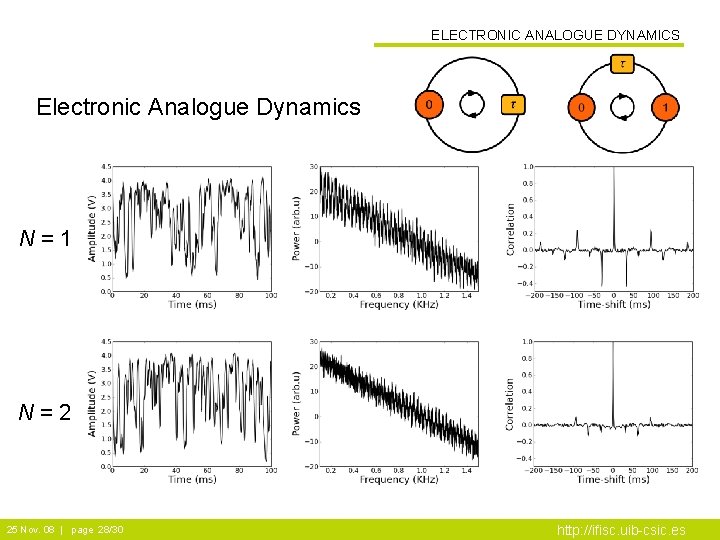
ELECTRONIC ANALOGUE DYNAMICS Electronic Analogue Dynamics N=1 N=2 25 Nov. 08 | page 28/30 http: //ifisc. uib-csic. es

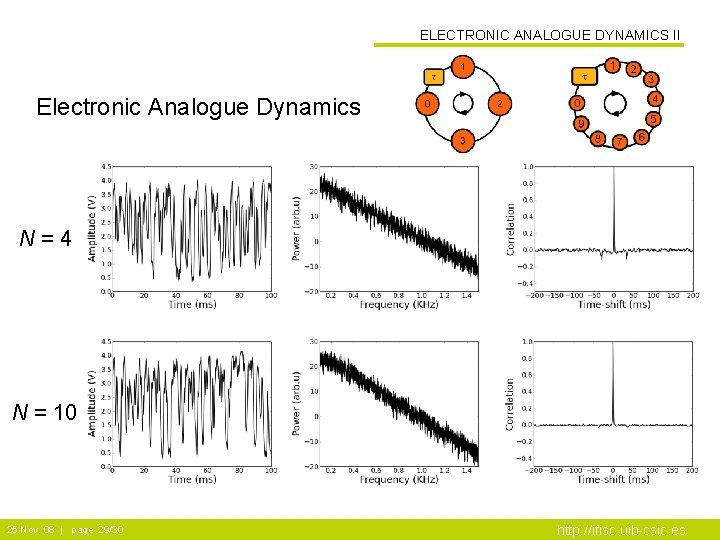
ELECTRONIC ANALOGUE DYNAMICS II Electronic Analogue Dynamics N=4 N = 10 25 Nov. 08 | page 29/30 http: //ifisc. uib-csic. es

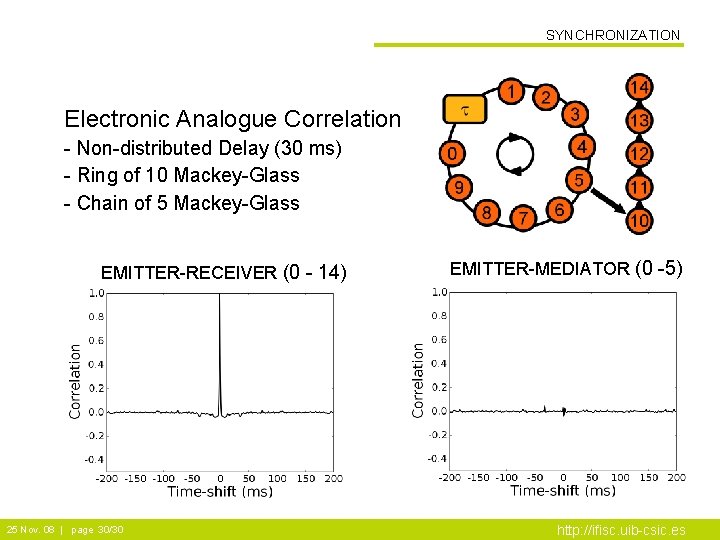
SYNCHRONIZATION Electronic Analogue Correlation - Non-distributed Delay (30 ms) - Ring of 10 Mackey-Glass - Chain of 5 Mackey-Glass EMITTER-RECEIVER (0 - 14) 25 Nov. 08 | page 30/30 EMITTER-MEDIATOR (0 -5) http: //ifisc. uib-csic. es

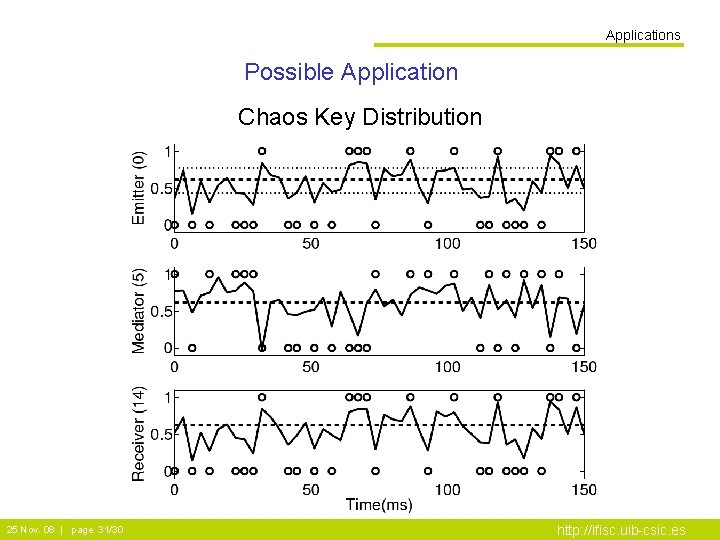
Applications Possible Application Chaos Key Distribution 25 Nov. 08 | page 31/30 http: //ifisc. uib-csic. es

RANDOM NUMBERS Generation of Random Bits Chaotic attractor Battery of Tests to check the “randomness” Frequency Test Pair Test Triple Test Gaps and Runs 25 Nov. 08 | page 32/30 http: //ifisc. uib-csic. es

THE END: CONCLUSIONS • Vanishing fingerprint of the delay with N • Increasing entropy with N • Synchronization among N/2 – 0 without correlation or mutual information via evaluating the cross correlation among N/2 & N’/2 • Practical implementation of key exchange via an uncorrelated mediator (mutual information close to zero) • Possible way to generate random bits • Extension to a larger number of elements 25 Nov. 08 | page 33/30 http: //ifisc. uib-csic. es