g2 phase study from GEANT simulation Qinzeng Peng

g-2 phase study from GEANT simulation Qinzeng Peng Advisor: James Miller Boston University Sep 28, 2004 Muon g-2 collaboration at BU: Lee Roberts, Rober Carey, Jon Paley, Xiaobo Huang Institutes: BU, BNL, UIUC, Univ. of Minnesota, Yale Univ. 1

Outline I. Brief introduction to g-2 II. Experimental set up and simulation III. Simulation results and analysis 2

What is g-2? magnetic moment gyromagnetic ratio spin • Dirac equation predicts g=2 • in nature radiative correction makes g≠ 2 where aμ(SM) = aμ(QED) + aμ(hadronic) + aμ(weak) aμ(New Physics) = aμ(Measured) − aμ(SM) Studied Muon instead of Electron due to 3

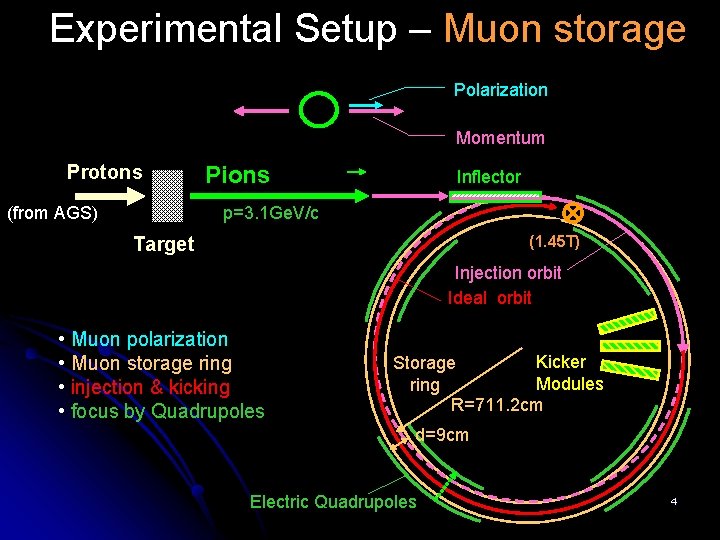
Experimental Setup – Muon storage Polarization Momentum Protons (from AGS) Pions Inflector p=3. 1 Ge. V/c (1. 45 T) Target Injection orbit Ideal orbit • Muon polarization • Muon storage ring • injection & kicking • focus by Quadrupoles Kicker Storage Modules ring R=711. 2 cm d=9 cm Electric Quadrupoles 4

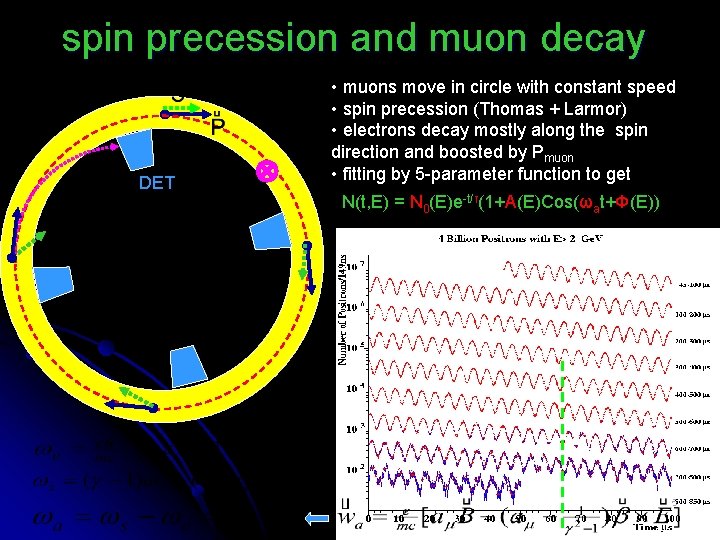
spin precession and muon decay DET • muons move in circle with constant speed • spin precession (Thomas + Larmor) • electrons decay mostly along the spin direction and boosted by Pmuon • fitting by 5 -parameter function to get N(t, E) = N 0(E)e-t/τ(1+A(E)Cos(ωat+Φ(E)) magic γ= 29. 3 5

Phase shift on ωa uncertainty What if φ is not a constant? Take an example: if And measuring time is about 600 μs, then 6

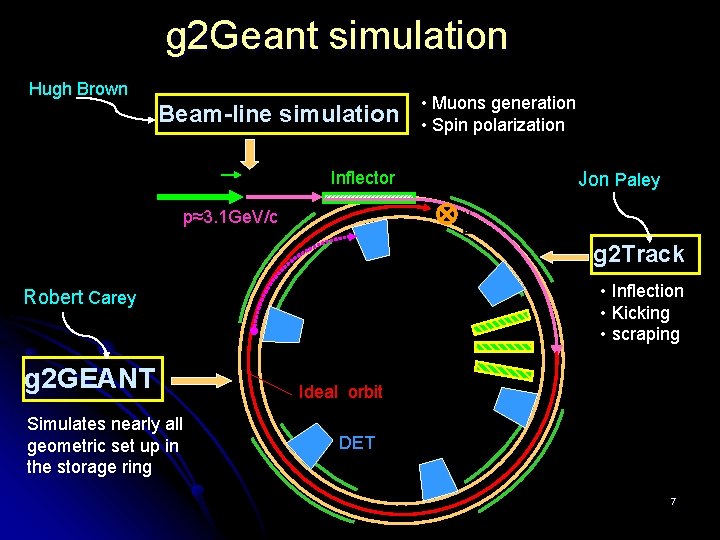
g 2 Geant simulation Hugh Brown Beam-line simulation Inflector • Muons generation • Spin polarization Jon Paley p≈3. 1 Ge. V/c g 2 Track • Inflection • Kicking • scraping Robert Carey g 2 GEANT Simulates nearly all geometric set up in the storage ring Ideal orbit DET 7

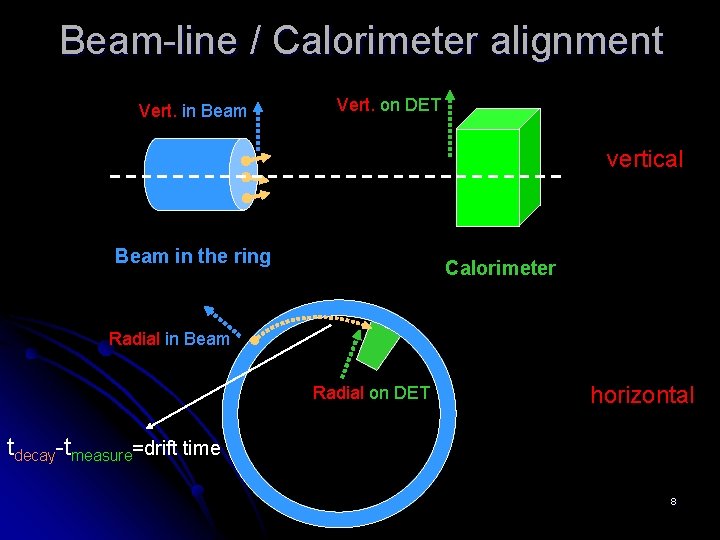
Beam-line / Calorimeter alignment Vert. in Beam Vert. on DET vertical Beam in the ring Calorimeter Radial in Beam Radial on DET horizontal tdecay-tmeasure=drift time 8

Data selection l l l Energy cut : En >1. 8 Ge. V Detector dependence : average over 24 detectors Drift time : offset of g-2 phase 9

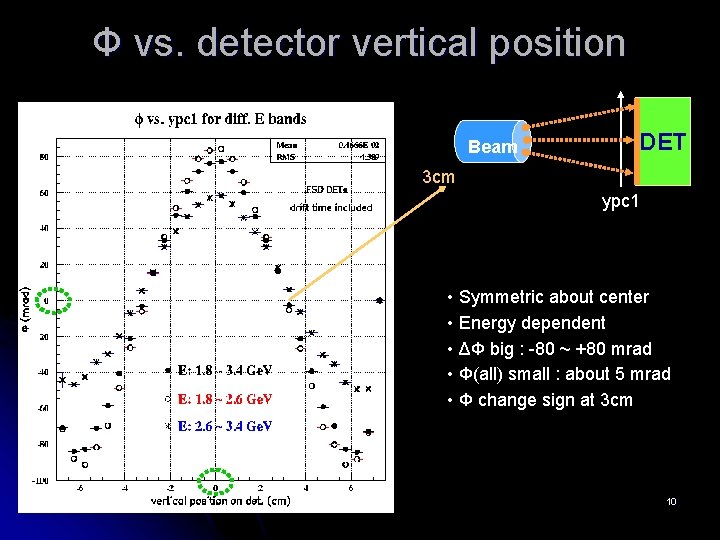
Ф vs. detector vertical position Beam DET 3 cm ypc 1 • Symmetric about center • Energy dependent • ΔΦ big : -80 ~ +80 mrad • Φ(all) small : about 5 mrad • Φ change sign at 3 cm 10

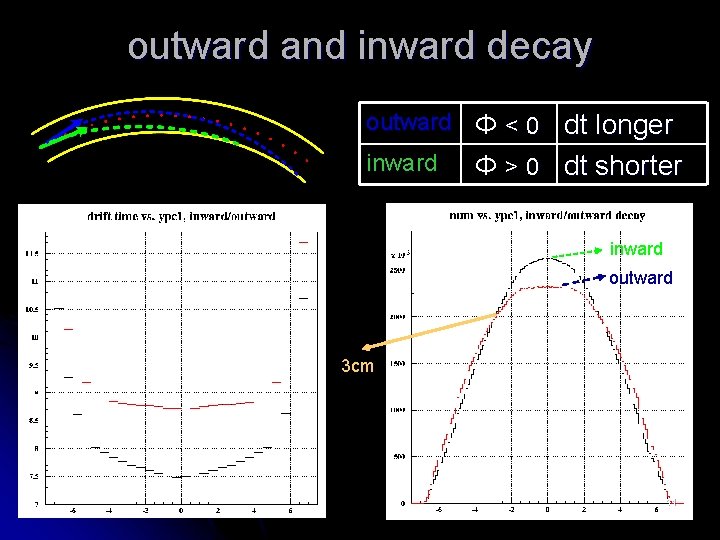
outward and inward decay outward Φ < 0 inward Φ>0 dt longer dt shorter inward outward 3 cm 11

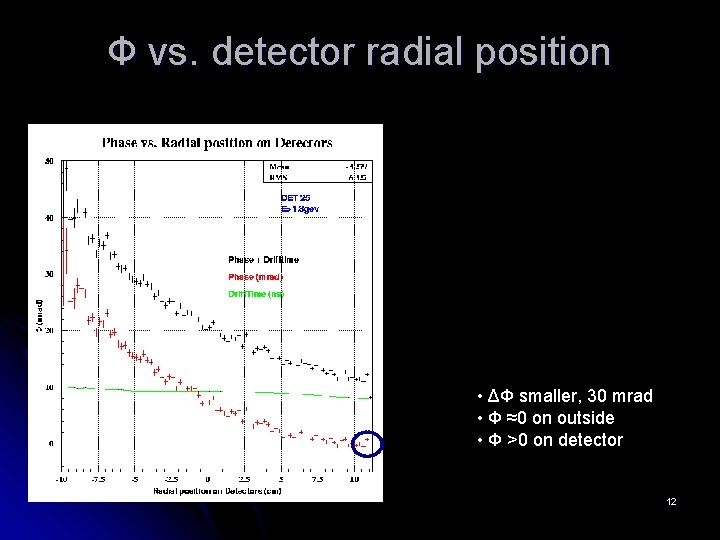
Ф vs. detector radial position • ΔΦ smaller, 30 mrad • Φ ≈0 on outside • Φ >0 on detector 12

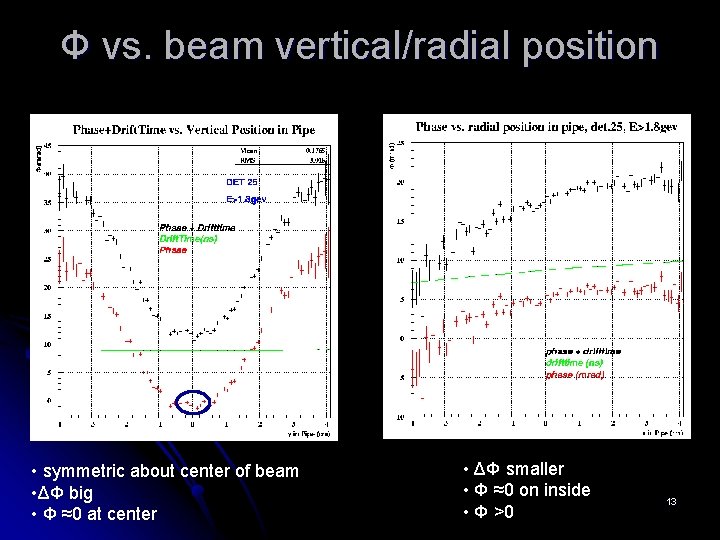
Ф vs. beam vertical/radial position • symmetric about center of beam • ΔΦ big • Φ ≈0 at center • ΔΦ smaller • Φ ≈0 on inside • Φ >0 13

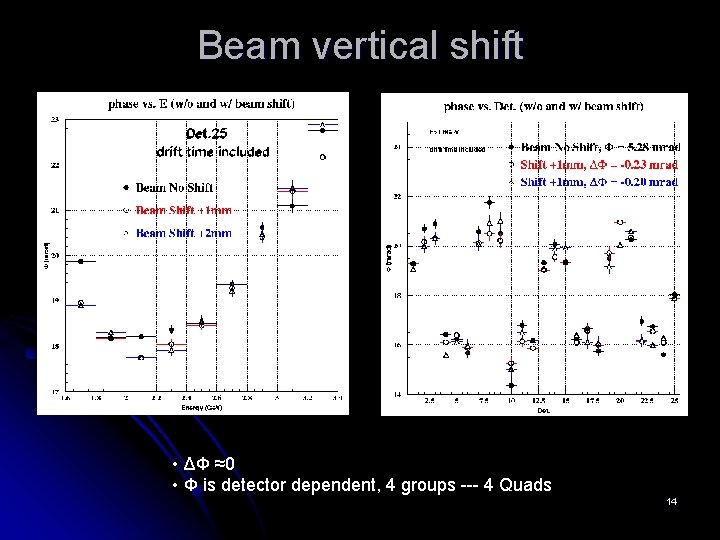
Beam vertical shift • ΔΦ ≈0 • Φ is detector dependent, 4 groups --- 4 Quads 14

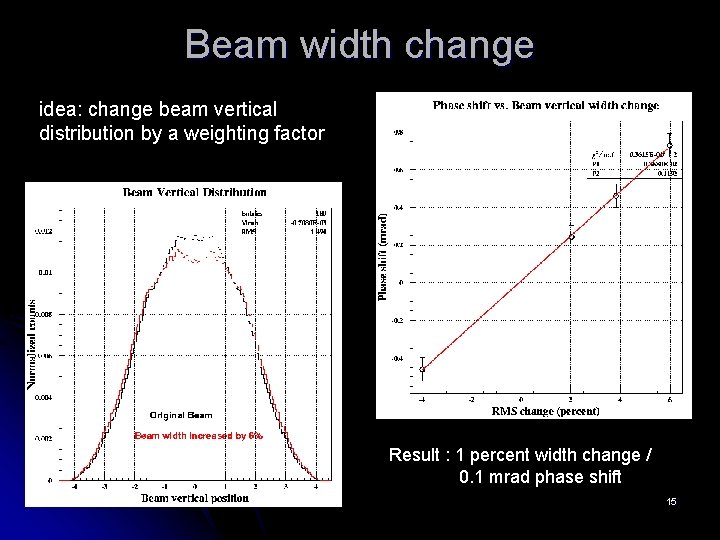
Beam width change idea: change beam vertical distribution by a weighting factor Result : 1 percent width change / 0. 1 mrad phase shift 15

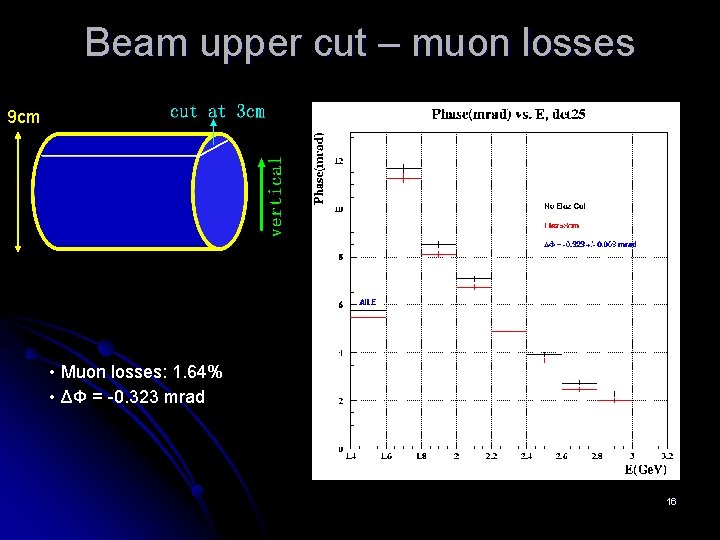
Beam upper cut – muon losses 9 cm • Muon losses: 1. 64% • ΔΦ = -0. 323 mrad 16

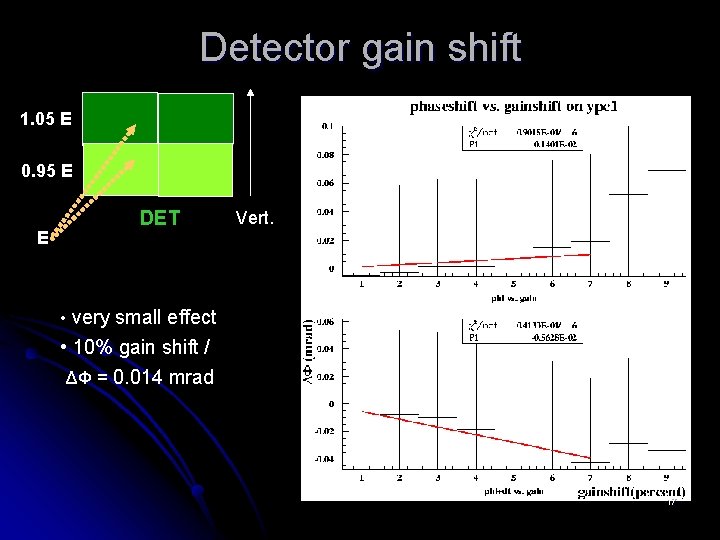
Detector gain shift 1. 05 E 0. 95 E E DET Vert. • very small effect • 10% gain shift / ΔΦ = 0. 014 mrad 17

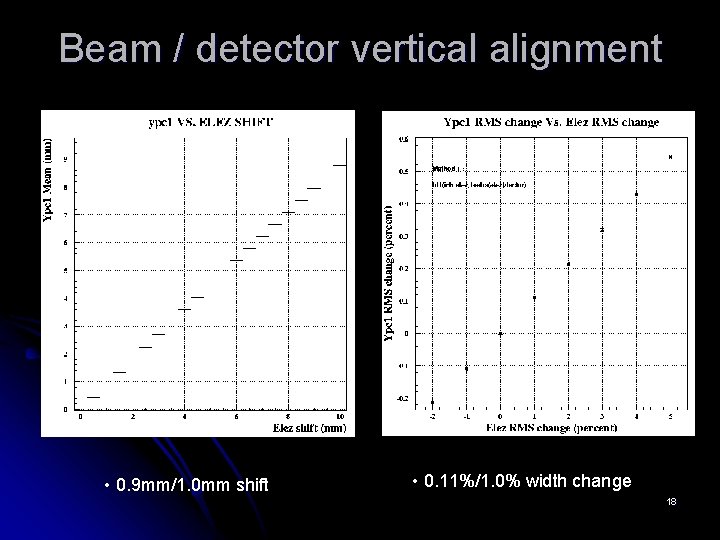
Beam / detector vertical alignment • 0. 9 mm/1. 0 mm shift • 0. 11%/1. 0% width change 18

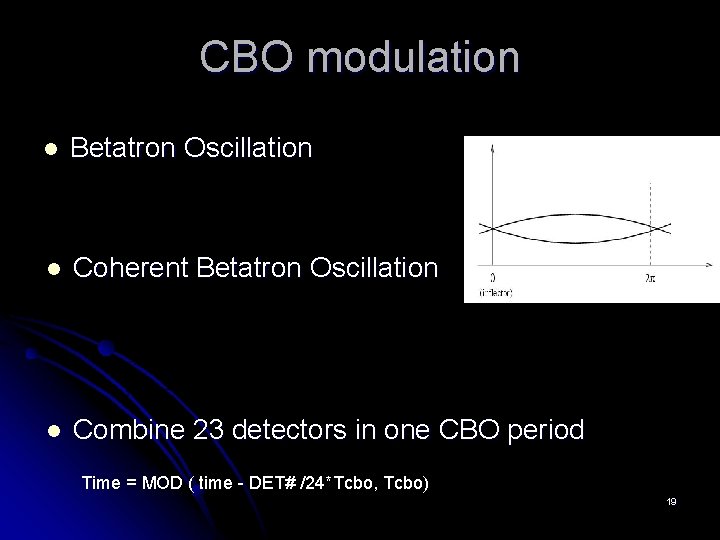
CBO modulation l Betatron Oscillation l Coherent Betatron Oscillation l Combine 23 detectors in one CBO period Time = MOD ( time - DET# /24*Tcbo, Tcbo) 19

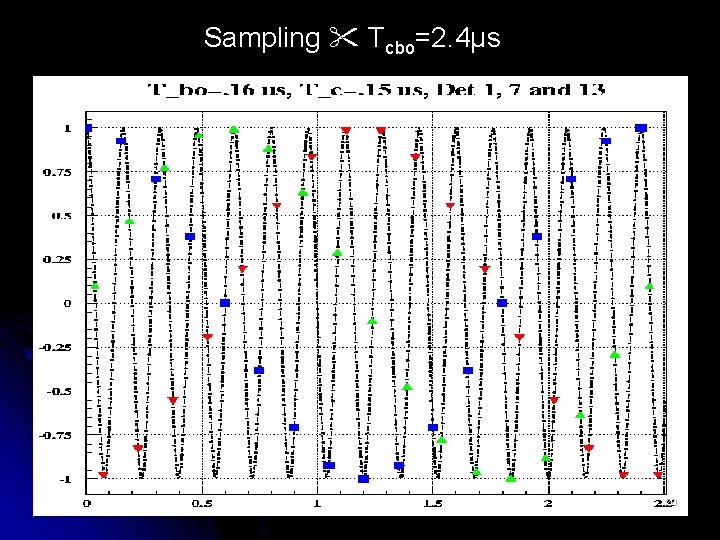
Sampling Tcbo=2. 4μs 20

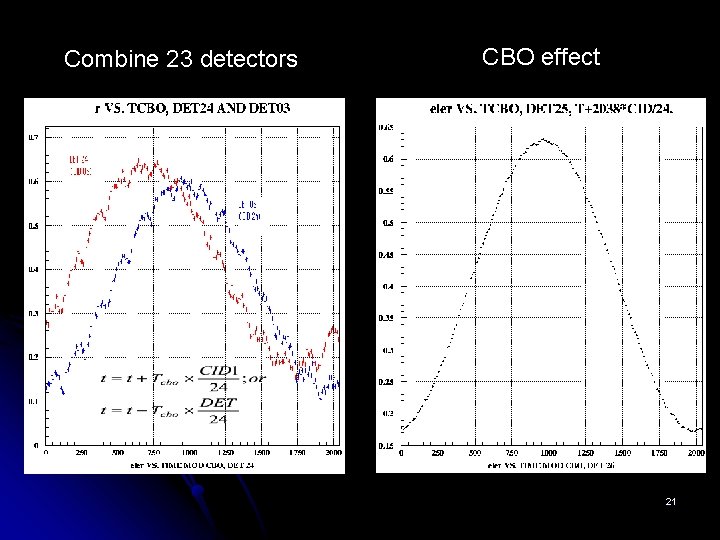
Combine 23 detectors CBO effect 21

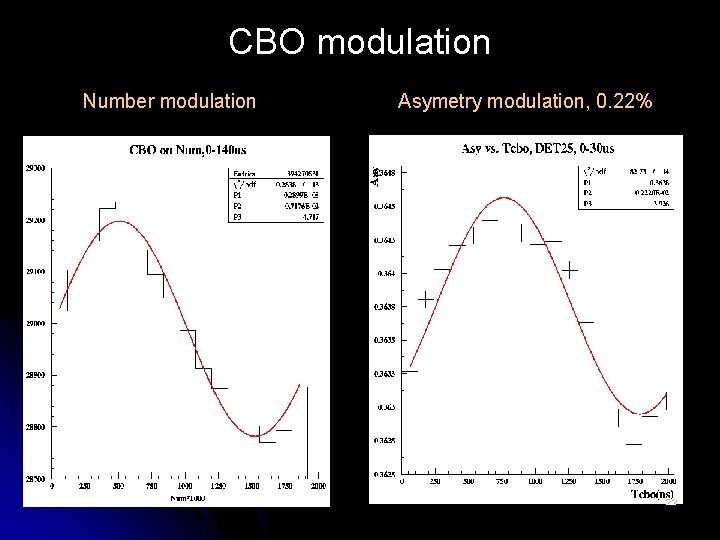
CBO modulation Number modulation Asymetry modulation, 0. 22% 22

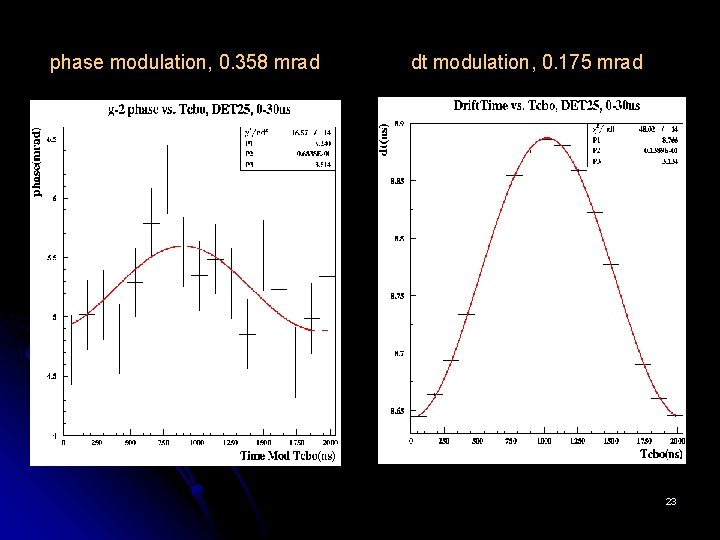
phase modulation, 0. 358 mrad dt modulation, 0. 175 mrad 23

conclusions Simulation results consistent with Real data, like FSD studies. l Phase shift due to the geometric set up is a small effect on ωa. l CBO effect is a small effect. l 24