FW 364 Ecological Problem Solving Class 4 Quantitative

FW 364 Ecological Problem Solving Class 4: Quantitative Tools Sept. 11, 2013

Outline for Today Objectives for Today: Survey how and why models are used Survey different categories of models Goal for Today: Help you to “get the gist” of modeling in general (we will go into more detail later about most models discussed today) Help you to understand what’s so special about this monkey

Quantitative Tools Why quantitative tools (math / models) are useful Quantitative tools: • make our process and assumptions transparent • help us to understand natural systems (can often be not intuitive) • allow us to do virtual experiments (cheaper than real experiments) • make predictions that can be tested in the real world • strengthen adaptive management (predictions, understand outcome)

Quantitative Tools Quantitative tools make our process and assumptions transparent Process examples: The DNR suggests a 25% reduction for walleye bag limit Models can be presented in reports and at public meetings that show exactly how the 25% reduction was calculated Models are helpful for showing that management decisions are not arbitrary Assumption examples: Mass balance: Steady-state assumption: Inputs = Outputs Predation: No predator saturation (satiation) Harvest: No reduction in angler effort with reduced bag limit Value: Other researchers / managers / stakeholders know how results were obtained

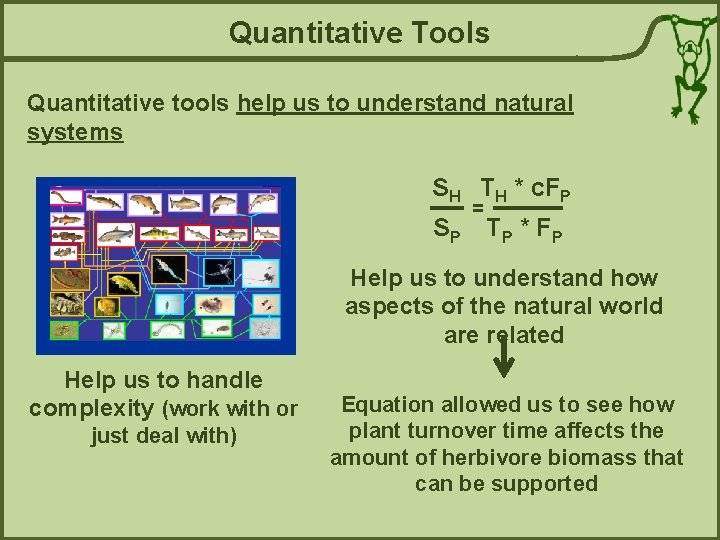
Quantitative Tools Quantitative tools help us to understand natural systems SH TH * c. FP = SP TP * F P Help us to understand how aspects of the natural world are related Help us to handle complexity (work with or just deal with) Equation allowed us to see how plant turnover time affects the amount of herbivore biomass that can be supported

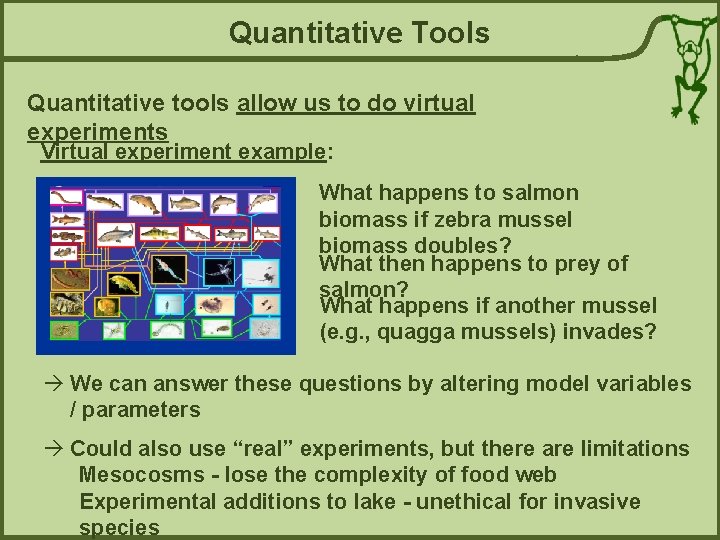
Quantitative Tools Quantitative tools allow us to do virtual experiments Virtual experiment example: What happens to salmon biomass if zebra mussel biomass doubles? What then happens to prey of salmon? What happens if another mussel (e. g. , quagga mussels) invades? à We can answer these questions by altering model variables / parameters à Could also use “real” experiments, but there are limitations Mesocosms - lose the complexity of food web Experimental additions to lake - unethical for invasive species

Quantitative Tools Number of Wolves Quantitative tools make predictions that can be tested in the real world 600 Built model of wolf population growth using 1999 -2007 data 500 400 300 200 100 0 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2000 1999 1998 Made predictions for 2008 -2012 from those data Year Predictions can now be evaluated in 2013 Models can be refined as needed would know if linear or non-linear was best model

Quantitative Tools Number of Wolves Quantitative tools strengthen adaptive management Hypothetically, say the 2008 -2012 data suggest population growth was linear Say our goal was 900 wolves by 2012 600 500 400 300 200 100 0 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2000 1999 1998 and we assumed in 2007 that population Year growth would be nonlinear à We adjust our model to include linear growth à Perhaps introduce more wolves to account for slower population growth

Components of Models Variables: the quantities that change in a model (y ) Dependent variable: The quantity that we want to estimate / predict E. g. , The amount of pollutant in the lake; population size Independent variables: variable being manipulated or followed ( x) E. g. , Time Functions: describe relationships between state variables E. g. , Lynx abundance is a function of hare abundance Lynx abundance = f (hare abundance) Could be linear function (y = a + bx) lynx abundance = a + b * hare abundance Parameters: constants that specify functions Mediate the relationship between independent and dependent variables Typically numbers that we can hopefully estimate with real data E. g. , Assimilation efficiency, per capita birth rate, survival

Model Complexity Model complexity range In general, different types of models fall somewhere along a simple-complex continuum Simple More general, behavior easy to understand (why the model predicts what it does), unrealistic Comple x More specific, realistic Example: Salmon stocking models Simple: Total # salmon in lake = f(# naturally reproduced, # stocked salmon) Complex: Total # salmon in lake = f(# naturally reproduced, # stocked salmon, competition, harvest, # prey, #

Model Complexity Which level of complexity do we use? Sometimes simple is best, some times complex, sometimes use both “Make everything as simple as possible, but not simpler” ~ Albert Einstein When the model is too complex, it can get very hard to understand the model results and connect them to assumptions There is no point in constructing a model that is an exact representation of nature… …would be as hard to understand as the system we're trying to model! But there is a tendency to want to consider all the factors

Pictorial Monkey Model Complexity Monkey Reality Monkey Model 1 Monkey Model 2 Monkey maybe DESIRED COMPLEXITY human?

Model Break! Let’s think about deer… http: //mvhs 1. mbhs. edu/mvhsproj/deer. html

Types of Models Model Categories: • • Static vs. Dynamic Discrete vs. Continuous Deterministic vs. Stochastic Analytical vs. Numerical Simulation

Static vs. Dynamic Static models assume system is at steady state E. g. , mass balance; predator and prey populations at carrying capacities Often much easier to use: can build an equation for steady state as function of different parameters & see how parameters affect equilibrium e. g. , how attack rate of predator affects carrying capacity Dynamic models provide a trajectory of some variable over time Can be used to predict both trajectories and equilibria More powerful, but more complex; Dynam e. g. , population size over time Population size ic Static Equilibrium Time Carryin g capacit y

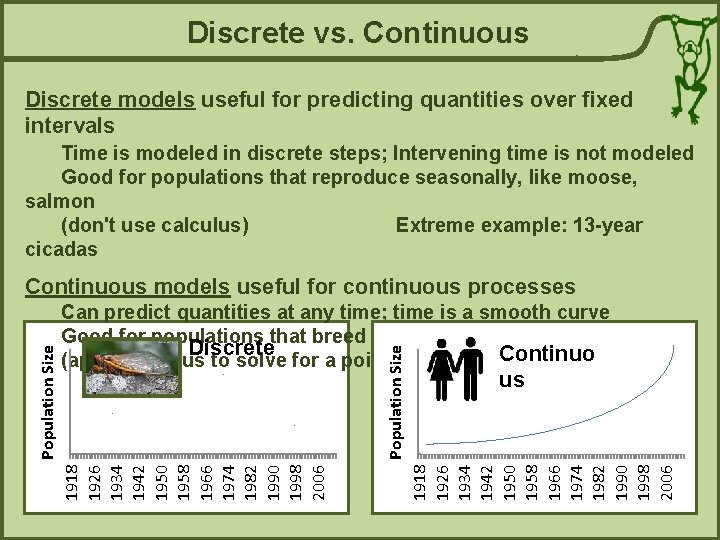
Discrete vs. Continuous Discrete models useful for predicting quantities over fixed intervals Time is modeled in discrete steps; Intervening time is not modeled Good for populations that reproduce seasonally, like moose, salmon (don't use calculus) Extreme example: 13 -year cicadas us 1918 1926 1934 1942 1950 1958 1966 1974 1982 1990 1998 2006 Population Size Can predict quantities at any time; time is a smooth curve Good for populations that breed continuously, like humans Discrete Continuo (apply calculus to solve for a point in time) 1918 1926 1934 1942 1950 1958 1966 1974 1982 1990 1998 2006 Population Size Continuous models useful for continuous processes

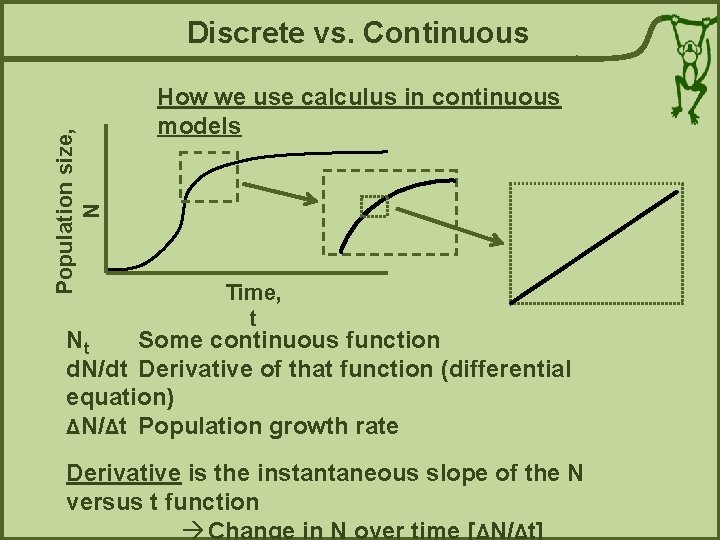
Population size, N Discrete vs. Continuous How we use calculus in continuous models Time, t Nt Some continuous function d. N/dt Derivative of that function (differential equation) ΔN/Δt Population growth rate Derivative is the instantaneous slope of the N versus t function à Change in N over time [ΔN/Δt]

Deterministic vs. Stochastic Deterministic models useful for making exact predictions (no uncertainty) Stochastic models have uncertainty or error built in

Deterministic vs. Stochastic Deterministic models useful for making exact predictions (no uncertainty) E. g. , population will be 5, 564 in 3 years y = a + bx Very simple deterministic model if we want to know y (dependent variable), we simply plug in values for a, b (parameters or constants) and then vary x (x will often be time) Advantage of Deterministic Models: Great as general tools for understanding ecological problems because they are simpler and easier to understand than stochastic models Drawback of Deterministic Models:

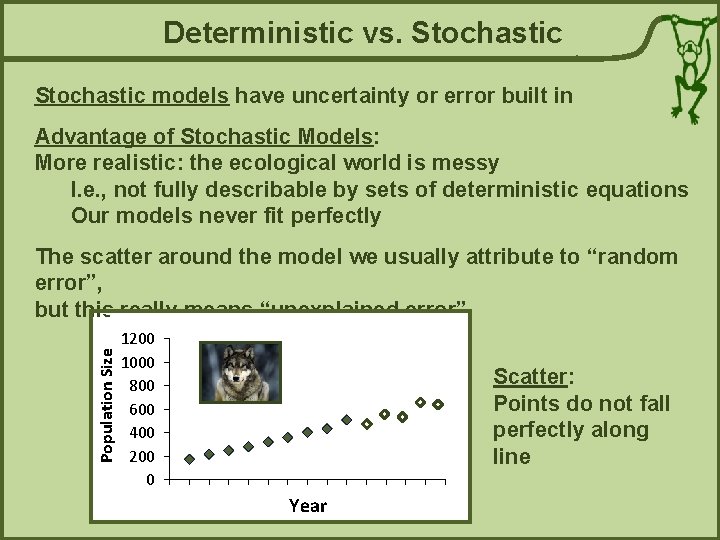
Deterministic vs. Stochastic models have uncertainty or error built in Advantage of Stochastic Models: More realistic: the ecological world is messy I. e. , not fully describable by sets of deterministic equations Our models never fit perfectly Population Size The scatter around the model we usually attribute to “random error”, but this really means “unexplained error” 1200 1000 800 600 400 200 0 Scatter: Points do not fall perfectly along line Year

Deterministic vs. Stochastic models have uncertainty or error built in Advantage of Stochastic Models: More realistic: the ecological world is messy I. e. , not fully describable by sets of deterministic equations Our models never fit perfectly y = a + bx + error Stochastic model example Prediction (y) is based on a, b, x and error (stochasticity) Model predicts a range (cloud of points) for y (not a single value for each x) Using statistics we can put bounds on the likely values of y E. g. , in 5 years we predict there will be between 1000 and 1500 wolves in the UP with 95% confidence

Analytical vs. Numerical Simulation Analytical models can be solved using algebra and calculus These are functions we are familiar with from math courses More general (can be applied in many contexts) e. g. , All our mass balance problems (T = S/F) Some dynamic models (e. g. , exponential population growth) Numerical simulation models cannot be solved using algebra and calculus Either because they have discontinuous functions Or because there are too many variables E. g. , Stochastic models (have “randomness” involved) Need a computer to solve iteratively: Plug in starting values (real numbers) Computer calculates output for each time step Advantage of Numerical Simulation Models: Greater realism, easier to use with available software (don't need to be a math whiz)

Analytical vs. Numerical Simulation Example: Equation series without an analytical solution Fluid dynamics around a boat hull Computers are used to plug in different combinations of numbers for the variables to determine what combinations work to make the equations balance à We’ll create complex conceptual models in Stella and let Stella do numerical simulations for us to solve them

Types of Models Where do our mass-balance models fit into these categories? Model Categories: • Static vs. Dynamic • Discrete vs. Continuous … why? • Deterministic vs. Stochastic • Analytical vs. Numerical Simulation

Types of Models Where do our mass-balance models fit into these categories? Model Categories: • Static vs. Dynamic Steady state (no time component) • Discrete vs. Continuous …why? No time component • Deterministic vs. Stochastic No uncertainty • Analytical vs. Numerical

Wrap-Up Monday: Starting population growth Chapter 1 in Text (if you want to read) Nt+1 = Nt