Fuzzy Topology Quantization and Longdistance Gauge Fields SSss

Fuzzy Topology, Quantization and Long-distance Gauge Fields SSss S. Mayburov Hep-th 1205. 3019 Quantum space-time and novel geometries: Discrete (lattice) space-time – Fundamental Plank length lp ( Snyder, 1947; Markov, 1948) Noncommutative geometry (Connes, 1991) Supergeometry (Rothstein, 1986) Hypothesis: Some geometries can induce also novel formalism of quantization (S. M. , 2008)

of List of Quantization Formalisms: SSss i) Schroedinger quantization: S state Ψ is vector (ray) in Hilbert space H ii) Operator algebra (C* algebra) : S observables constitute nonassociative operator algebra U iii) Symbols of operators ( Segal, 1948) (Berezin, 1970) … etc. , …) Geometric Formalism - why not ? Possible applications : Quantum Gravity

S Sets, Topology and Geometry Example: Fundamental set of 1 -dimensional Euclidian geometry is (continious) ordered set of elements X = { xl } ; xi xl - points xj X

p. PPpp. Partial ordered set – P u B Beside , it can be also: xi ~ xj - incomparabilty relation u 1 D Dx u 1 xxi X = { x l } - ordered subset; - incomparable point X ST - total set; ST = X Pu P u = { uj } - partial ordered subset Example: let’s consider interval i Fu 1 ~ xk , u 1 , xk are incomparable (equivalent) ST elements

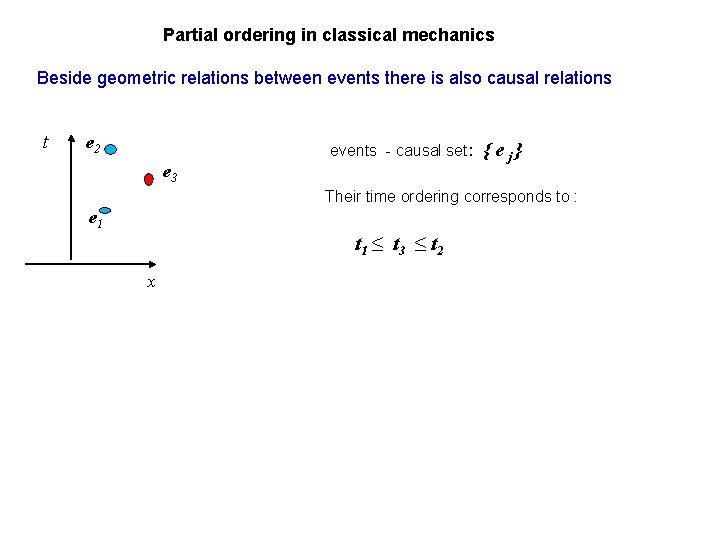
Partial ordering in classical mechanics Beside geometric relations between events there is also causal relations t e 2 events - causal set: e 3 { e j} Their time ordering corresponds to : e 1 t 1 ≤ t 3 ≤ t 2 x

Partial ordering in classical mechanics Beside geometric relations between events there is also causal relations t e 2 events - causal set: e 3 { e j} Their time ordering corresponds to : e 1 t 1 ≤ t 3 ≤ t 2 x if one event dynamically induces another : e 1 → e 2 If to describe also causal relations between events: e 1 ≤ e 2 ; e 1 ~ e 3 ; e 2 ~ e 3 So e 3 is incomparable in causal terms to e 1 and e 2

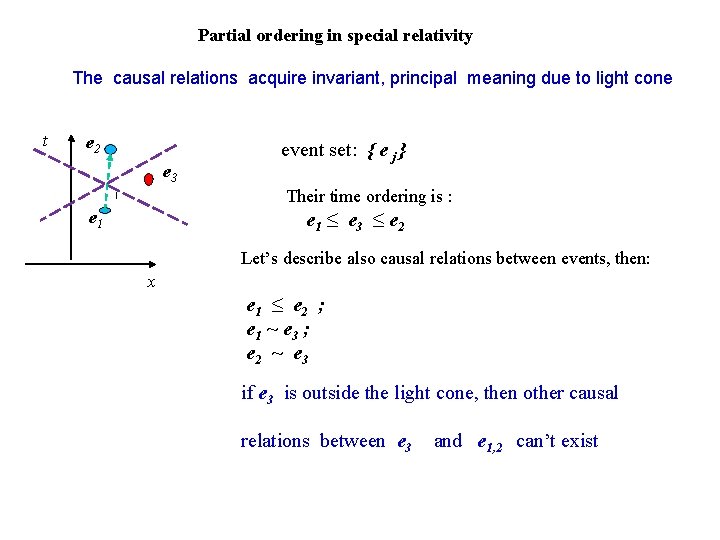
Partial ordering in special relativity The causal relations acquire invariant, principal meaning due to light cone t e 2 e 3 event set: { e j } Their time ordering is : e 1 ≤ e 3 ≤ e 2 Let’s describe also causal relations between events, then: x e 1 ≤ e 2 ; e 1 ~ e 3 ; e 2 ~ e 3 if e 3 is outside the light cone, then other causal relations between e 3 and e 1, 2 can’t exist

Fuzzy ordered set (Foset) - F ={ fi } If f j - fuzzy points, then: if Ffi , fk , (Zeeman, 1964) ~ fk wi, k >0 , F ={f i} - set of fuzzy points; Σ wjk =1 EExample: ST - total set w 1 i ST = X F; F={ f 1 } X – ordered subset f 1 . _ . . xi Ffi ~ xk , . X wi, k >0 , Σ wjk =1

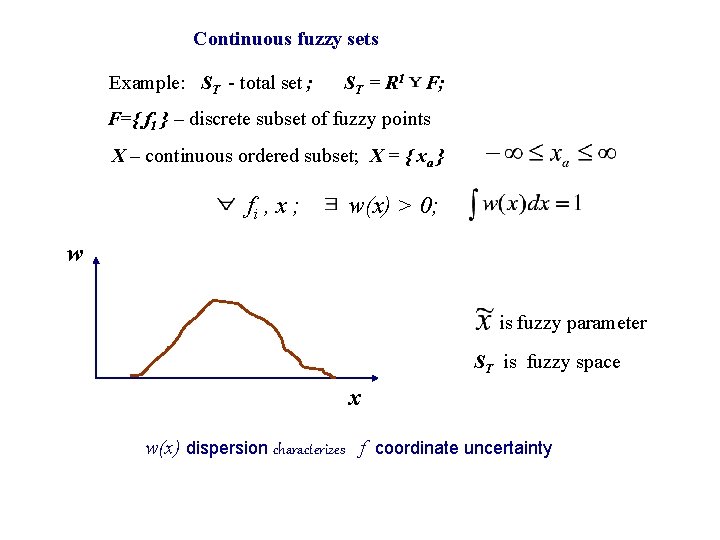
Continuous fuzzy sets EExample: ST - total set ; ST = R 1 F; F={ f 1 } – discrete subset of fuzzy points X – continuous ordered subset; X = { xa } fi , x ; w(x) > 0; w is fuzzy parameter ST is fuzzy space x w(x) dispersion characterizes f coordinate uncertainty

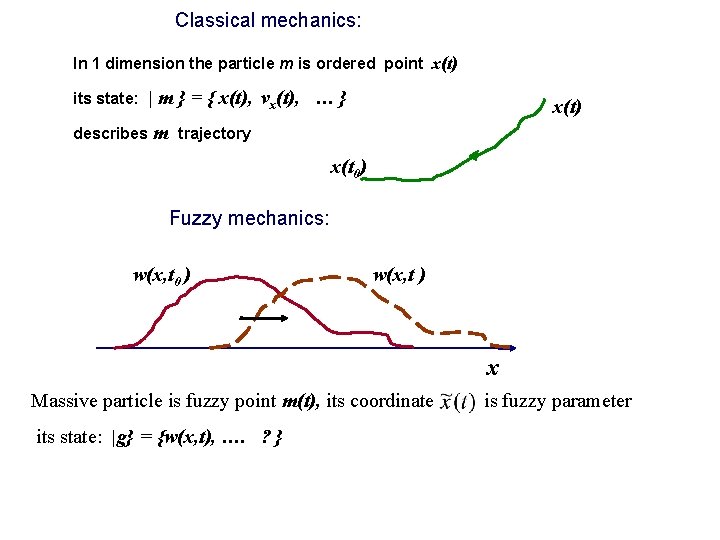
Classical mechanics: In 1 dimension the particle m is ordered point x(t) its state: | m } = { x(t), vx(t), … } describes m x(t) trajectory x(t 0) Fuzzy mechanics: w(x, t 0 ) w(x, t ) x Massive particle is fuzzy point m(t), its coordinate its state: |g} = {w(x, t), …. ? } is fuzzy parameter

Fuzzy evolution in 1 -dimension Fuzzy state | g } : | g}= {w(x), q 1 , q 2 … } w(x, t 0 ) X Beside w(x, t), another |g} parameter is we shall look for | g} free parameters assuming represented as real functions qi(x, t) - average m velocity that they can be

Fuzzy Evolution Equations Let’s consider free w(x, t) evolution : Suppose that w(x, t) evolution is local and so can be described as: where then from w(x) norm conservation: f - arbitrary function hhh

Fuzzy Evolution Equations Let’s consider free w(x, t) evolution : Suppose that w(x, t) evolution is local and so can be described as: where then from f - arbitrary function w(x, t) norm conservation: if to substitute : then: If this condition is fulfilled, then : - 1 -dimensional flow continuity equation hhh

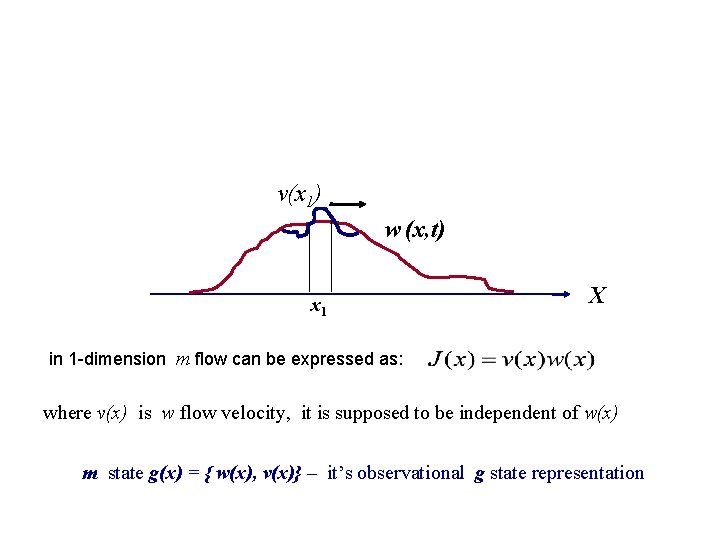
v(x 1) w (x, t) x 1 X in 1 -dimension m flow can be expressed as: where v(x) is w flow velocity, it is supposed to be independent of w(x) m state g(x) = { w(x), v(x)} – it’s observational g state representation

for m state g = { w(x), v(x)}, we substitute v(x) by related parameter: k is theory constant ; c is arbitrary real number so m state is: g = { w(x), α(x)}, then g ~ g(x) = g 1 (x) + ig 2(x) we suppose that g(x) is normalized, so that g(x)g* (x) = w(x), yet g(x) is still arbitrary complex function: where for any is arbitrary real function the set of g(x) constitutes complex Hilbert space H

We suppose that observables Correct are linear, self-adjoint operators on H g(x) ansatz should give all values to be independent of c value To derive it it ‘s enough to consider flow (current) operator Then : It follows that the only g(x) ansatz which give independent of c value is written as : This is standard quantum-mechanical ansatz value to be

Evolution Equation for Fuzzy state We start with linear operator g(x) for fuzzy dynamics, later the nonlinear operators will be considered also For free m motion H should be invariant relative to space shifts so: It means that H can be only polinom: j can be only even numbers, j = 2, 4, 6, … because noneven j contradict to X -reflection invariance

Equation for operator From flow equation: it follows: ffr hence: and

Equation for operator From flow equation: and it follows: ffr hence: and: From comparison of highest α derivatives it follows n=2; fuzzy state g(x, t) obeys to free Schroedinger equation with mass m = k !

Nonlinear evolution operator Bargman - Wigner theorem (1964) : g(t 0 ) → g’(t) If arbitrary pure state evolves only into the pure state and module of scalar product for all pure states |< ψ|φ >| is conserved, then the evolution operator is linear. Jordan (2006): If for all g(t 0 ) : g(t 0 ) → g’(t) i. e. if all pure states evolve only to pure ones, and is defined unambiguously, then is linear operator Yet fuzzy pure states g(x, t) evolve only to pure ones, so their evolution should be linear g(x, t) are normalized complex functions, we obtained free particle’s quantum evolution on Hilbert space H Origin of the results : w(x, t) flow continuity is incompatible with the presence of high x - derivatives in g evolution equation

We didn’t suppose that our theory possesses Galilean invariance, II in fact, Galilean transformations can be derived from fuzzy dynamics, if to suppose that any RF corresponds to physical object with

Assuming the formalism extension to relativistic invarince, Let’s assume that the formalism can be extended to relativistic invariance In this case the flow continuity equation is fulfilled: Starting from it and demanding that w(x, t)>0 It results in the linear equation for 4 -spinor which is Dirac equation : Its fuzzy space: F = { } is double (entangled) fuzzy structure

Fuzzy space: F = { } generates Hilbert space H of complex functions g(x, t) which describe particle’s evolution in F Observables are linear, self-adjoint operators on H particle’s momentum: commutation relations follow from geometrical and topological properties, so in this approach fuzzy topology induces such operator algebra What about ? and Modified fuzzy space them F supposedly can be underlying structure for

Fuzzy States and Secondary Quantization Example: Fock free quantum field { nk } in 1 -dimension e - particle numbers can be regarded as fuzzy values each particle possesses fuzzy coordinate - double fuzzy structure

Interactions in Fuzzy Space Free Schroedinger equation: is equivalent to system of two equations for real and imaginary parts of I) - flow continuity equation II ) here I) is kinematical equation, it describes w(x, t) balance only

Interactions in Fuzzy Space Free Schroedinger equation: is equivalent to system of two equations for real and imaginary parts of - flow continuity equation I) II ) + Hint here I) is kinematical equation, it describes w(x, t) balance only Hence particle’s interactions can be included only in II) But it supposes their gauge invariance, because is quantum phase

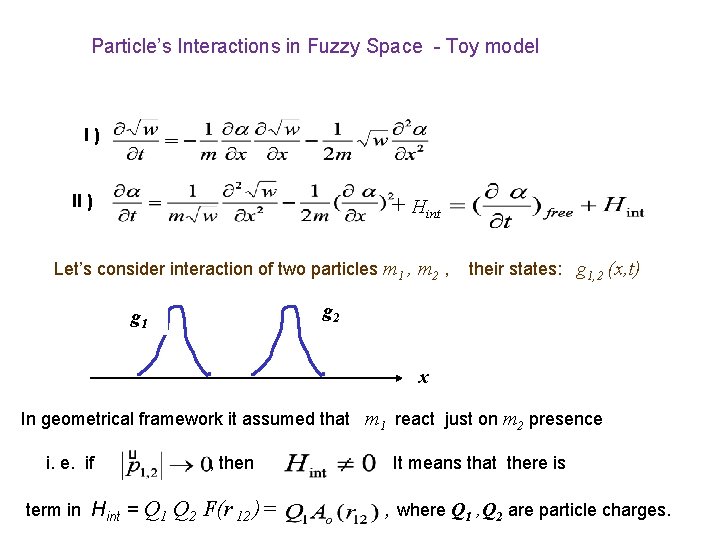
Particle’s Interactions in Fuzzy Space - Toy model I) II ) + Hint Let’s consider interaction of two particles m 1 , m 2 , their states: g 1, 2 (x, t) g 2 g 1 x In geometrical framework it assumed that m 1 react just on m 2 presence i. e. if term in Hint = , then Q 1 Q 2 F(r 12 )= It means that there is , where Q 1 , Q 2 are particle charges.

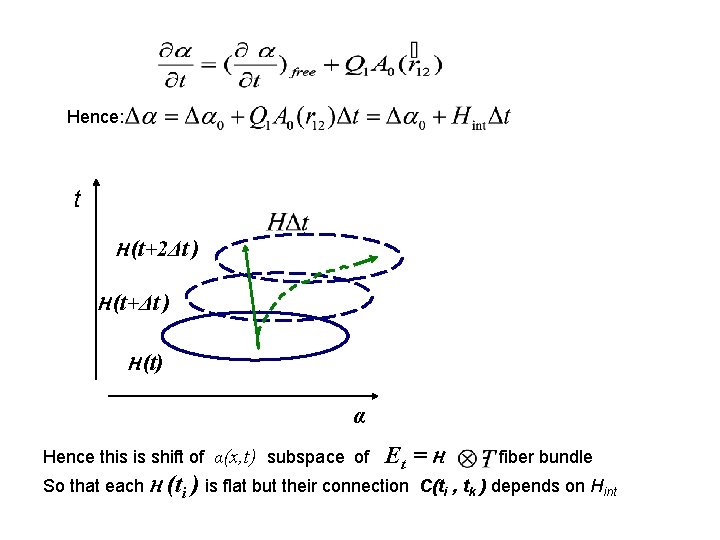
Hence: ttt t H (t+2Δt ) H (t+Δt ) H (t) α Hence this is shift of α(x, t) subspace of So that each H Et = H (ti ) is flat but their connection - fiber bundle C(ti , tk ) depends on Hint

(Non)locality of interactions on fuzzy space We supposed that in our model the interactions are local, yet such theory is generically nonlocal, two particles with fuzzy coordinates can interact nonlocally; Fermions with fuzzy coordinates can nonlocally interact with bosonic field.

Conclusions 1. 1. Fuzzy topology is simple and natural formalism for introduction of quantization into any physical theory 2. Shroedinger equation is obtained from simple assumptions, Galilean invariance follows from it. 3. Local gauge invariance of fields corresponds to dynamics on fuzzy manifold

Fuzzy Topology, Quantization and Gauge Fields S. Mayburov hep-th 1205. 3019 To explore quantum space-time it can be important to describe Quantum physics and space-time within the same mathematical formalism Proposed approaches: i) To extend quantum operator algebras on space-time description: Noncommutative Geometry (Connes, 1988), etc. ; Applications to Quantum Gravity (Madore, 2005) ii) To extend some novel geometry on quantum physics: Possible approach: Geometry equipped with fuzzy topology (S. M. , 2007)

Fuzzy Correlations We exploit fuzzy state: Yet more correct expression is : here: Correlation of g(x) state between its components x, x’ appears due to particle fuzziness on X axe, it defines g(x) free evolution: Such ansatz corresponds to quantum density matrix More complicated correlations can appear in fuzzy mechanics.

Particle’s Interactions on fuzzy manifold let’s suppose that two identical particles m 1 , m 2 repulse each other Deflections of m 1 motion induced by m 2 presence at some distance, even if ; yet for and + Hint Hence: this is deformation of m 1 fiber bundle H

Particle’s Interactions in Fuzzy Space suppose that m 1 is described by Klein-Gordon equation with E>0 and m 2 is classical particle, i. e. m 2 If in initial RF: then: For Lorenz transform RF to RF’ with velocity where : only such vector field and makes transformation consistent So this toy-model is equivalent to Electrodynamics if Aμ is massless field

Fuzzy state for fermion (iso)doublet Consider D fermion (iso)spin doublet of mass m 0 Fuzzy parameters: Fuzzy representation: ; particle’s state : z g = - linear representation - (iso)spin vector from Jordan theorem ψs evolution should be linear

Nonabelian case: Yang-Mills Fields Consider interaction of two femions m 1 , m 2 of D that their interaction is universal, so that at doublet and suppose it gives - isospin vectors To agree with global isotopic symmetry, two isospin vectors in nonrelativistic limit can interact with each other only via this ansatz: s 1 s 2 Hence: and so : For nonrelativistic QCD limit it gives: But it supposes that local gauge invariance follows from global isotopic symmetry : - Yang-Mills

Yang-Mills Interactions Suppose that m 1 is described by Klein-Gordon equation with E>0 and m 2 is classical particle, i. e. m 2 so m 2 generates classical ; and Yang-Mills field in initial RF: For Lorenz transform RF to RF’ with velocity where : only such vector field and makes transformation consistent So we obtain standard Yang-Mills Hamiltonian for particle-field interaction

We derived free particle’s dynamics from some geometrical and set-theoretical axioms. Is it possible to describe particle’s interactions in the same framework ? We exploited m states: g = { w(x), α(x)} defined in flat Hilbert space H Analogously to general relativity, in geometry euipped with fuzzy topology the interactions induce the deformation of H and H fiber bundle

Fuzzy Mechanics and Gauge Invariance In QFT local gauge invariance is postulated. We shall argue that in Fuzzy mechanics it can be derived from global isotopic invariance

Such formalism need only three axioms, whereas standard QM is based on seven axioms i) Particles are points of fuzzy manifold, their states are characterized by two parameters |g } = { w(x, t), v(x, t) } ii) Observables Q are supposed to be linear, self-adjoint operators on H iii) Reduction (Projection) postulate for result of Q measurement In this model Plank constant is just coefficient, which connects x and px scales, so Relativistic unit system gives its natural description

Content 1. Geometric properties induced by structure of fundamental set 2. Partial ordering of points, fuzzy ordering, fuzzy sets 3. Fuzzy manifolds and physical states 4. Derivation of Shroedinger dynamics for fuzzy states 5. Interactions on fuzzy manifold and gauge fields For simplicity only 1+1 geometry will be considered

Particle’s Interactions in Fuzzy Space - Toy model I) II ) + Hint Let’s consider interaction of two particles m 1 , m 2 , their states: g 1, 2 (x, t) g 2 g 1 x In geometrical framework it’s natural to assume that Hint is universal, i. e. if , then there is term in Hint ~ It means that Q 1 Q 2 F(r 12 ), where Q 1 , Q 2 are particle’s charges.

Relativistic Evolution Equation we suppose that fuzzy state: and: || w || =1 If we look for 1 st order evolution equation: where: If tw. III then for the unique solution is: n=2 , i. e. Schroedinger evolution

Fuzzy evolution and linearity We don’t assume that w(x, t ) is linear function of w(x’, t 0 ) which is standard assumption of classical kinetics w(x, t 0 ) w(x, t ) Δ 1 X Example : Boltzman diffusion

Clocks, proper times and partial ordering In special relativity each dynamical system has it is its own proper time, there is no universal time, so proper time connected with clock dynamics of given reference frame (RF) ta tb Constraint: each event time t 1 in one RF is mapped to the point on time axe in other RF t’ 1 e 1 ~ e 3

It can be transformed to symmetric complex g representation in H It can be proved that only such g(x) representation corresponds to consistent dynamics g(x) → { w(x), v(x)} is unambiguous map α(x) is analogue of quantum phase

m particle’s state |g} = { w(x), α(x) } The problem : to find dynamical |g} representation g(x, t) : is dynamical operator (Hamiltonian) We have two degrees of freedom: g = { w(x), α(x) }, it can be transferred to: g(x) = g 1 (x)+ ig 2 (x) such that g 1 (x), g 2 (x) = 0, if w(x) = 0 This is symmetric g representation example:

Generalization of event time mapping one can substitute points by δ-functions ta ~ e 3

Fuzzy dynamics – space symmetry restoration as the possible fundamental low of dynamics E Global symmetries are important in quantum physics Free particle m: w 0(x): space shift symmetry is broken w(t) X Low of fuzzy evolution : space symmetry of m state |g} is restored as fast as possible : So free m evolution U(t) : w 0(x) const at very large t Interactions: to restore space symmetry two identical particles e 1 , e 2 should repulse each other

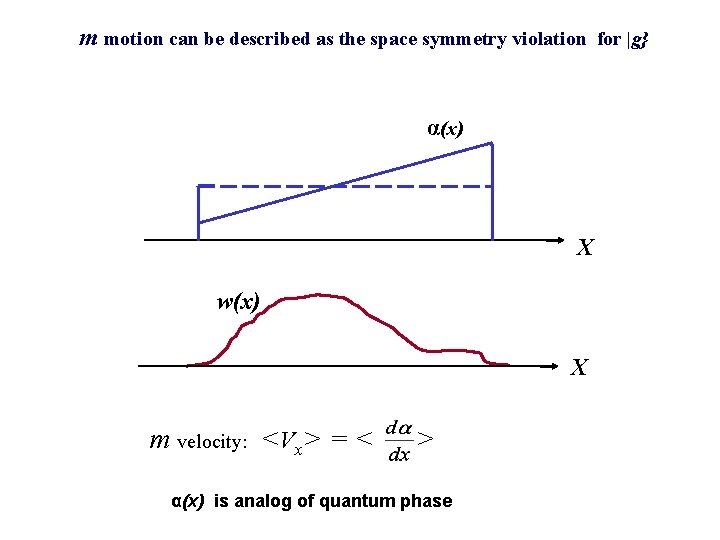
m motion can be described as the space symmetry violation for |g} fffffff α(x) X w(x) X m velocity: <Vx> = < d > α(x) is analog of quantum phase

hence w flow equation can be written as: v(x 1 ) v(x 2 ) Δ 1 Δ 2 X

Fuzzy mechanics – space symmetry restoration as the general low of free motion hello ggggggkggghfh